Лекция №2
Отношения и функции
Определение. Упорядоченной парой < x, y > называется совокупность, состоящая из двух элементов x и y, расположенных в определенном порядке. Две пары < x, y > и < u, v > считаются равными тогда и только тогда, когда x = u и y = v.
Определение. Бинарным или двуместным отношением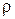 
называют множество упорядоченных пар. Элементы x и y называют координатами или компонентами отношения .
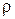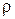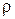Записи < x, y >Î и x y означают, что пара < x, y > принадлежит бинарному отношению 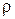(или x, y находятся в отношении ).
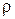Определение. Областью определения бинарного отношения 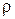называют множество D r={ x | для которых существует такое y, что x 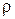y }. Областью значений 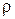называют множество R r={ y | для которых существует такое x, что x 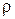y }.
Примеры.
1. Множество {<1,2>,<2,4><3,3>,<2,1>} – бинарное отношение.
D r={1, 2, 3}, R r={2, 4, 3, 1}={1, 2, 3, 4}.
2.{< x, y > | x, y – действительные числа и x = y } – множество, задающее отношение равенства на множестве R действительных чисел (специальное обозначение «=»).
D r={ x | x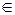 
R }, R r={ y | y 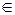R }.
3.{< x, y > | x, y – целые числа, для которых найдется положительное целое число z такое, что x + z = y } – отношение «меньше чем» на множестве целых чисел (обозначение «<»).
D r и R r – множество целых чисел.
Аналогично можно построить множества, задающие отношения «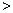
», «
», « ».
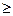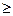Определение. Упорядоченным набором длины n называется после-довательность, состоящая из n элементов x 1, x 2, x 3,…, xn, распо-ложенных в определенном порядке. Обозначается < x 1, x 2, x 3,…, xn >. Два набора длины n < x 1, x 2, x 3,…, xn > и <y1, y2, y3,…, y n > считаются равными тогда и только тогда, когда xi = y i,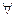 
i = 1, 2,…, n. Определение. n -нарным отношением называют множество упорядоченных наборов длины n.
Произведение множеств
Определение. Пусть даны n множеств A 1, A 2,…, An. Множество всех упорядоченных наборов < x 1, x 2,…, xn > таких, что x 1Î A 1,…, xn Î An называют прямым (или декартовым) произведением множеств A 1, A 2,…, An и обозначают A 1´ A 2´…´ A n или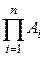 
.
Произведение одинаковых множеств называется прямой степенью, обозначается An.
При n =2 X ´ Y ={< x, y > | x Î X, y Î Y }.
Каждое бинарное отношение r есть подмножество прямого произведения двух множеств, так что D rÍ X и R rÍ Y. Если X = Y то говорят, что r есть отношение на множестве X.
Примеры.
1. Пусть X ={0,1}, Y ={ x, y }. Тогда
X ´ Y ={<0, x >, <0, y >, <1, x >, <1, y >};
Y ´ X ={< x,0 >, < x,1>, < y,0>, < y,1>}.
2. Пусть X ={1,2,3}, Y ={0,1}. Тогда
X ´ Y ={<1,0>,<1,1>,<2,0>,<2,1>,<3,0>,<3,1>};
Y ´ X ={<0,1>,<0,2>,<0,3>,<1,1>,<1,2>,<1,3>}.
(Отметим, что X ´ Y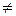 
Y ´ X, если X 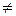Y.)
К бинарному отношению «=» принадлежит одна пара <1,1>.
К отношению «<» в множестве Y ´ X принадлежат все пары, кроме <1,1>. В множестве X ґ Y таких пар нет.
3. X = R, Y = R, тогда X ´ Y = Y ´ X = R ´ R.
R ´ R – множество точек плоскости x 0 y (R – множество всех действительных чисел).
4. Пусть X = { x | x 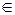[0,1]}, Y = { y | y 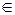[1,2]}.
Тогда
X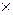 
Y = {< x, y > | x 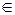[0,1], y 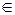[1,2]} – множество точек квадрата (рис. 2.1).
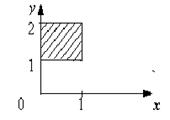
Рис. 2.1. Множество X 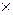Y
5. Если А = { a, b }, C = Æ, то A ´ C = C ´ A = Æ.
Для бинарных отношений определены обычным образом операции объединения, пересечения и т.д.
Дополнением бинарного отношения r между элементами А и В считается множество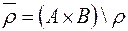 
.
Определение. Обратным отношением для бинарного отношения r={< x, y > | < x, y >Îr} называется отношение r-1={< y, x > | < x, y >Îr}.
Примеры. 1.В качестве примера можно рассмотреть числовую функцию, как бинарное отношение, заданное на числовых множествах. В этом случае обратная функция будет играть роль обратного бинарного отношения.
2. Зададим на множестве спортсменов отношение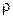 
: «быть ниже ростом» или 
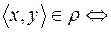спортсмен x ниже ростом, чем спортсмен y. Обратным к 
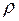будет отношение 
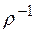: «быть не ниже ростом».
Определение. Композицией отношений r1 и r2 называют отношение r2or1={< x, y > | для которых $ z такое, что < x, z >Îr1 и < z, y >Îr2}.
(Композиция – это последовательное преобразование x ® z, z®y)
Свойства бинарных отношений
1. 
.
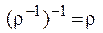2. 
.
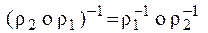Доказательство п. 2.
Из определения обратного отношения утверждение < y, x >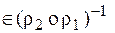 
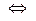< x, y >Î(r2or1),
а это из определения композиции равносильно тому, что
$ z | < x, z >Îr1 и < z, y >Îr2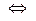
(из определения обратного отношения)
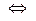$ z | < z, x >Îr1-1 и < y, z >Îr2-1 или (если переставить местами)
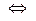$ z |< y, z >Îr2-1 и < z, x >Îr1-1, что по определению композиции равносильно тому, что < y, x >Î(
).
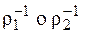Сравнивая с исходным соотношением, убеждаемся в справедливости равенства 2.
Функции
Определение. Бинарное отношение f называется функцией, если для всех x, y, z из условий < x, y >Î f и < x, z >Î f следует, что y = z. (Функция является однозначной).
Две функции равны, если они состоят из одних и тех же элементов. Область определения: Df, область значений: Rf.
Если Df = X и Rf = Y, то говорят, что f осуществляет отображение множества X на множество Y. Обозначения:
f: X ® Y или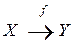 
.
< x, y >Î f Û y = f (x); где y – образ элемента x при отображении f, x – прообраз элемента y.
Примеры.
{<1,2>, <2,3>,< a, b >} – функция (так как каждому значению x соответствует определенное значение y);
{<1,2>,<1,3>,<2,4>} – не функция (1 отображается сразу на два элемента);
{< x, x 2+2 x +1> | x 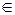R } – функция y = x 2+2 x +1.
Определение. n -местной функцией или функцией n переменных называют отношение f, отображающее множество всех наборов из n элементов множества X (прямое произведение n множеств) на множество Y, т.е. f: Xn ® Y. Обозначение y = f (x 1,…, xn).
Определение. Функция f: X ® Y называется инъективной, если для любых x 1, x 2, и y таких, что одновременно y = f (x 1) и y = f (x 2), справедливо равенство x 1= x 2
" x 1, x 2, y | y = f (x 1), y = f (x 2) Þ x 1= x 2.
(Т. е. одинаковые значения y могут соответствовать только одинаковым значениям x, что означает однозначность обратного отношения).
Заметим, что функция, отображающая друг на друга линейно упорядоченные множества (в частности, числовая функция), может быть инъективной лишь в случае её строгой монотонности
Определение. Функция f: X ® Y называется сюръективной, если для " y Î Y $ x Î X | y = f (x). (Т. е. каждому значению y соответствует некоторое хотя бы одно значение x).
Определение. Функция f называется биективной (или биекцией), если f одновременно сюрьективна и инъективна.
Говорят, что биективная функция f осуществляет взаимно однозначное соответствие между множествами X и Y.
Примеры. Рассмотрим функции, осуществляющие отображение 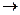R 
R:
f (x)=e x – инъективна (строго монотонна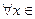 
R), но не сюръективна при x 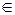R (т.к. 
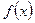не принимает отрицательных значений и 
,);
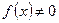f (x)= x 3- x – сюръективна, но не инъективна (для y =0 имеем три разных значения x);
f (x)=2 x +1, f (x)= x 3+ x – биективны (всюду определены и строго монотонны).
Утверждение. Композиция двух функций есть функция.
Доказательство. Допустим, композиции g o f принадлежат две пары:
.
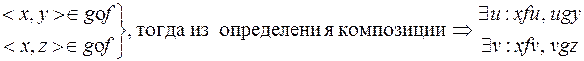Поскольку f – функция, то из ее определения u = v. Поскольку g – функция и u = v, то y = z, т.е. g o f – по определению функция.
Утверждение. Композиция двух биективных функций есть биективная функция. Следует из взаимной однозначности отображений, осуществляемых биективными функциями.
Определение. Тождественным отображением множества X в себя называется отображение
ex: X ® X такое, что " x Î X, ex (x)= x (образ совпадает с прообразом).
Аналогично, тождественным отображением множества Y в себя называется отображение
ey: Y ® Y такое, что " y Î Y, ey (y)= y.
Тогда справедливы следующие соотношения f o ex = f, ey o f = f.
Утверждение. Отображение f: X ® Y имеет обратное отображение f -1: Y ® X тогда и только тогда, когда f – биекция.
Доказательство.
Прямое утверждение. Пусть f – биекция. Поскольку
f – сюръективна, то обратное отношение f -1 определено на множестве Y (каждому y соответствует определенное x).
В связи с инъективностью функции f обратное отношение f -1 однозначно, т.е. является функцией (так как функция – однозначна, а инъективность означает невозможность соответствия различных x одному y). Прямое утверждение доказано.
Обратное утверждение. Пусть теперь отображение f имеет обратное отображение – f -1, определенное на множестве Y со значениями во множестве X. Тогда f сюръективно (для всех y существует x). Так как f -1 – функция, т.е. однозначна (для каждого y существует определенное x), то это означает инъективность f, как обратного отношения.
Следовательно, f – биекция. Утверждение доказано.
Замечание. Для того, чтобы обратное отношение f -1 было функцией на множестве значений Rf функции f, достаточно, чтобы функция f была инъективной (выполнялась однозначность обратного отношения f -1).
Тогда для инъективных функций выполняются следующие свойства бинарных отношений
1) (f -1)-1= f;
2) (g o f) -1= f -1o g -1.