Это метод решения линейных и нелинейных уравнений с одним неизвестным. Он называется также методом касательных или методом линеаризации. Если хn есть некоторое приближение к корню  , а f (x) имеет непрерывную производную, то уравнение f (x) = 0 можно преобразовать следующим образом:
, а f (x) имеет непрерывную производную, то уравнение f (x) = 0 можно преобразовать следующим образом:
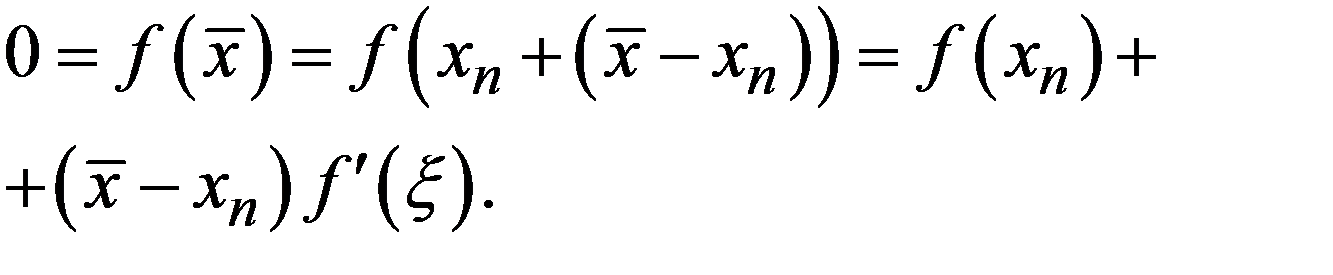
Приближенно заменяя 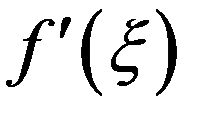 на значение в известной точке хn, получим такой итерационный процесс
на значение в известной точке хn, получим такой итерационный процесс
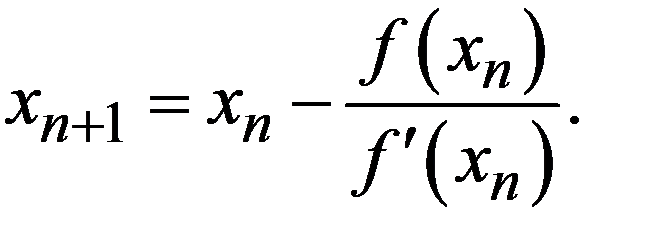 Выводится он из уравнения
Выводится он из уравнения 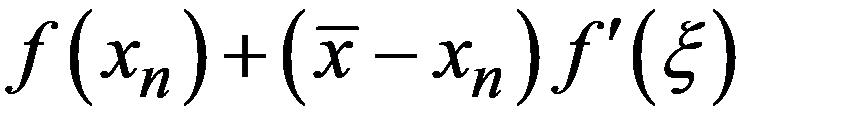 = 0,
= 0,
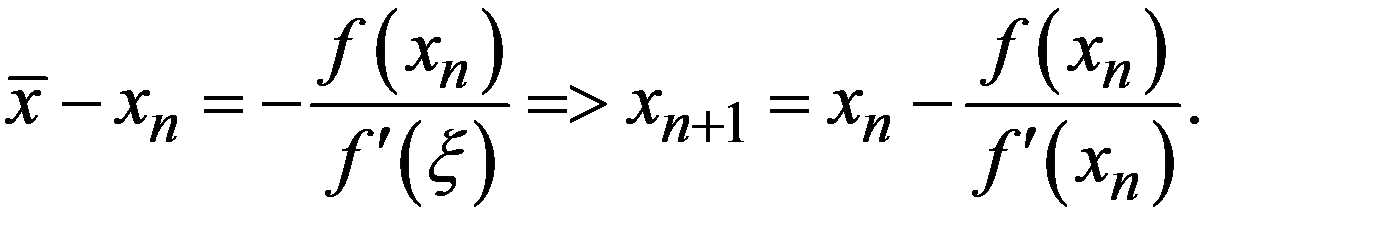
Метод Ньютона можно рассматривать как частный случай метода простых итераций, если положить 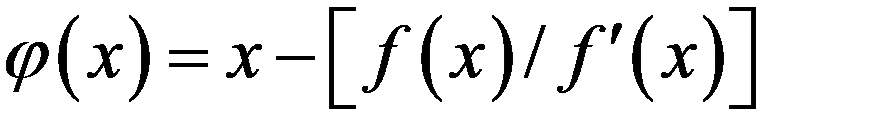 , На прошлой лекции у нас было сказано, что уравнение f (x) = 0 надо преобразовать к виду
, На прошлой лекции у нас было сказано, что уравнение f (x) = 0 надо преобразовать к виду 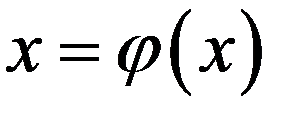 . Соотношение
. Соотношение 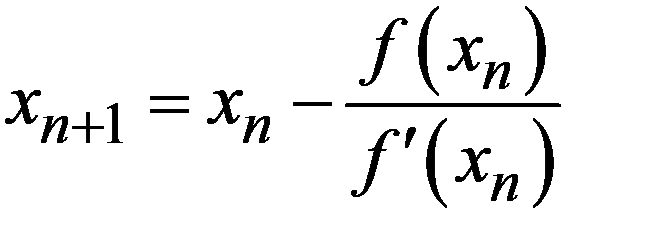
именно так и выглядит, если положить 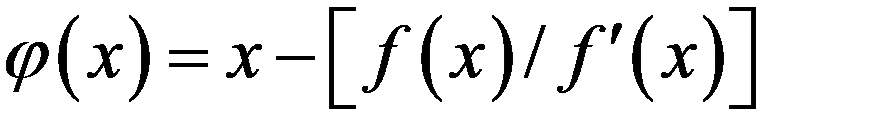 .
.
Тогда производная  Если
Если 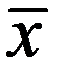 есть р -кратный корень уравнения f (x)=0, то вблизи него
есть р -кратный корень уравнения f (x)=0, то вблизи него 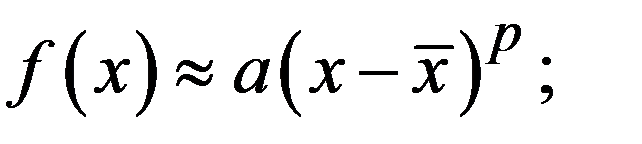 отсюда нетрудно получить
отсюда нетрудно получить 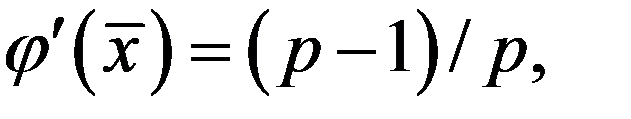 т.е.
т.е. 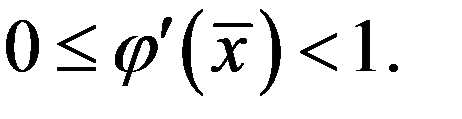 Для простого корня р = 1 и
Для простого корня р = 1 и 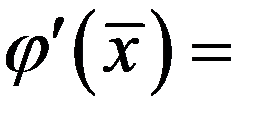 0. Отсюда можно сформулировать следующие условия сходимости итерационного метода Ньютона.
0. Отсюда можно сформулировать следующие условия сходимости итерационного метода Ньютона.  Если нулевое приближение выбрано достаточно близко к корню, ньютоновские итерации сходятся; скорость сходимости велика для простого корня и соответствует скорости геометрической прогрессии для кратного корня. При произвольном нулевом приближении итерации сходятся, если всюду
Если нулевое приближение выбрано достаточно близко к корню, ньютоновские итерации сходятся; скорость сходимости велика для простого корня и соответствует скорости геометрической прогрессии для кратного корня. При произвольном нулевом приближении итерации сходятся, если всюду  в противном случае сходимость будет не при любом нулевом приближении, а только в некоторой окрестности корня.
в противном случае сходимость будет не при любом нулевом приближении, а только в некоторой окрестности корня.
Сходимость вблизи любого корня монотонна, что легко видеть из рис. 17.1, но вдали от корня возможна немонотонность итераций. Отметим, что рис. 17.1 указывает еще на одно достаточное условие сходимости итераций.
| f (х 0) |
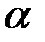
|
 х х
|
| х 3 |
| х 2 |
| х 1 |
| х |
| у |
| рис. 17.1 |
| х0 |
| f (х 1) |
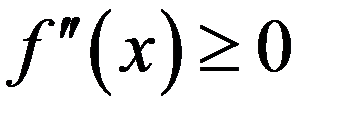 справа от корня, то на этом отрезке итерации сходятся, причем монотонно. То же будет, если
справа от корня, то на этом отрезке итерации сходятся, причем монотонно. То же будет, если  слева от корня на отрезке [ b,
слева от корня на отрезке [ b, 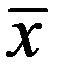 ], и на этом же отрезке выбрано нулевое приближение. Таким образом, итерации сходятся к корню с той стороны, с которой
], и на этом же отрезке выбрано нулевое приближение. Таким образом, итерации сходятся к корню с той стороны, с которой 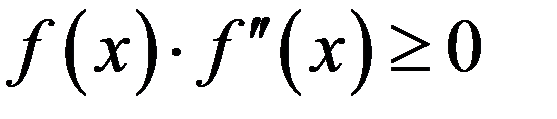 .
.
Оценим скорость сходимости вблизи простого корня. По определению простых итераций, 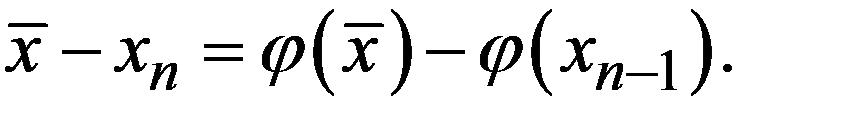 Разлагая правую часть по формуле Тейлора,
Разлагая правую часть по формуле Тейлора,

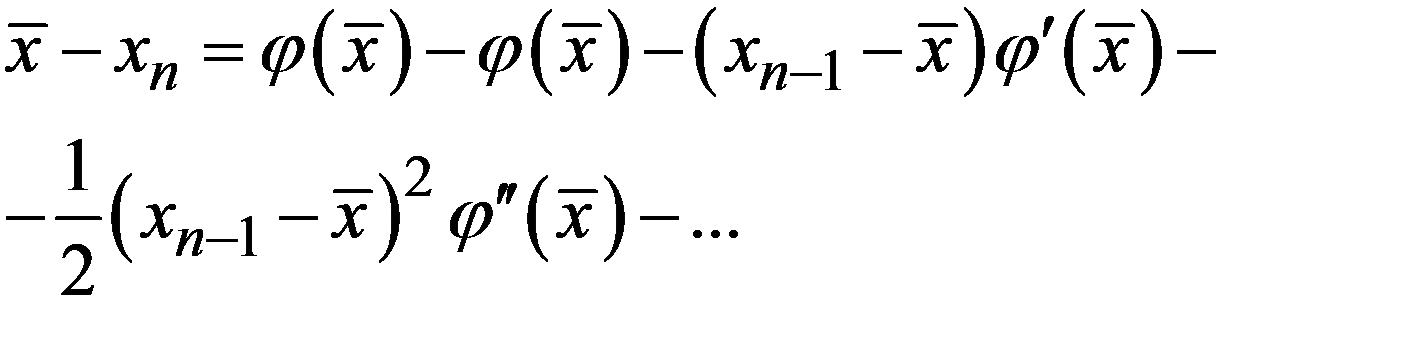
и, учитывая равенство 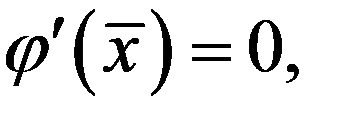 получим:
получим:
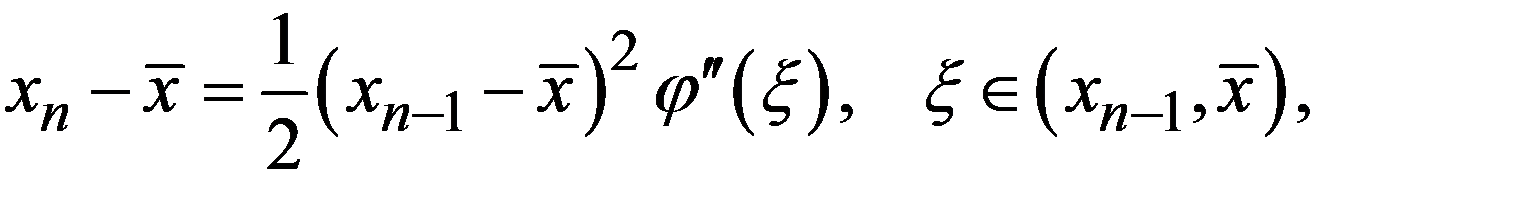 т.е. погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Например, если (n -1)-я итерация давала 3 верных знака, то n -я даст примерно 6 верных знаков, а (n +1) – примерно 12 знаков.
т.е. погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Например, если (n -1)-я итерация давала 3 верных знака, то n -я даст примерно 6 верных знаков, а (n +1) – примерно 12 знаков.
Это иллюстрирует быструю сходимость вблизи корня. Разумеется, вдали от корня подобные соображения неприменимы.
Если вычисляется корень высокой кратности, то 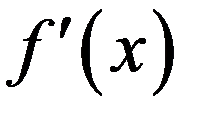 в знаменателе формулы Ньютона становится малой вблизи корня. Чтобы не было потери точности, отношение
в знаменателе формулы Ньютона становится малой вблизи корня. Чтобы не было потери точности, отношение 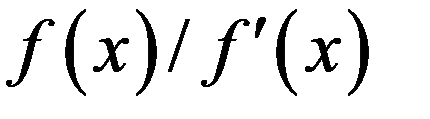 надо вычислять достаточно аккуратно. К остальным погрешностям расчета метод Ньютона хорошо устойчив.
надо вычислять достаточно аккуратно. К остальным погрешностям расчета метод Ньютона хорошо устойчив.
Для нахождения корней произвольной дифференцируемой функции чаще всего применяют метод Ньютона, особенно если известны разумные начальные приближения для корней.
Пример. Рассмотрим решение уравнения 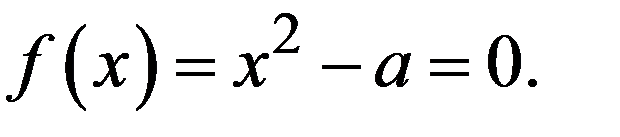 Тогда итерационная формула Ньютона принимает вид
Тогда итерационная формула Ньютона принимает вид

Мы получили вторую итерационную формулу для решения этого уравнения, представленную на прошлой лекции, которая, как отмечалось, позволяет очень быстро находить квадратный корень с помощью только сложения и деления. Для иллюстрации в таблице 17.1 приведен ход итераций при извлечении квадратного корня из а = 4.
Таблица 17.1
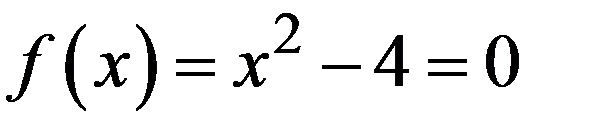
| ||
| n | 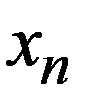 , метод Ньютона , метод Ньютона
| 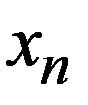 ,метод секущих ,метод секущих
|
| 2,5 2,05 2,0001 | 2,5 1,8571 1,9836 |
Видно, что сходимость очень быстрая; несмотря на неважное нулевое приближение, уже третья итерация дает точность 0,005 %.
Метод секущих
В методе Ньютона требуется вычислять производную функции, что не всегда удобно. Можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. Тогда вместо процесса Ньютона получим 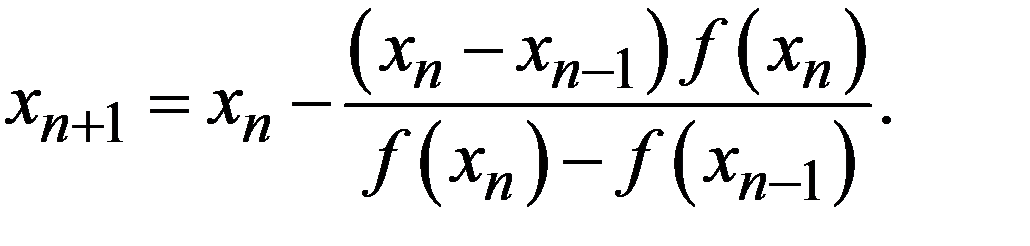 (17.1)
(17.1)
Для начала процесса надо задать 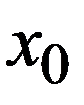 и
и 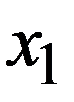 (рис. 17.2). Такие процессы, где для вычисления очередного приближения надо знать два предыдущих, называют двухшаговыми. Эти, казалось бы, небольшие изменения сильно влияют на характер итераций. Например, сходимость итераций может быть немонотонной не только вдали от корня, но и в малой окрестности корня. Скорость сходимости также изменяется. Иллюстрацией служит приведенный в таблице 17.1 расчет по методу секущих; для удобства сравнения с методом Ньютона первые два приближения взяты одинаковыми. Видно, что метод секущих сходится медленнее.
(рис. 17.2). Такие процессы, где для вычисления очередного приближения надо знать два предыдущих, называют двухшаговыми. Эти, казалось бы, небольшие изменения сильно влияют на характер итераций. Например, сходимость итераций может быть немонотонной не только вдали от корня, но и в малой окрестности корня. Скорость сходимости также изменяется. Иллюстрацией служит приведенный в таблице 17.1 расчет по методу секущих; для удобства сравнения с методом Ньютона первые два приближения взяты одинаковыми. Видно, что метод секущих сходится медленнее.
Таблица 17.1
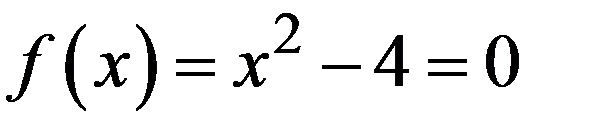
| ||
| n | 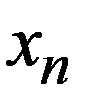 , метод Ньютона , метод Ньютона
| 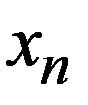 ,метод секущих ,метод секущих
|
| 2,5 2,05 2,0001 | 2,5 1,8571 1,9836 |
Скорость сходимости можно оценить, разлагая все функции в (17.1) 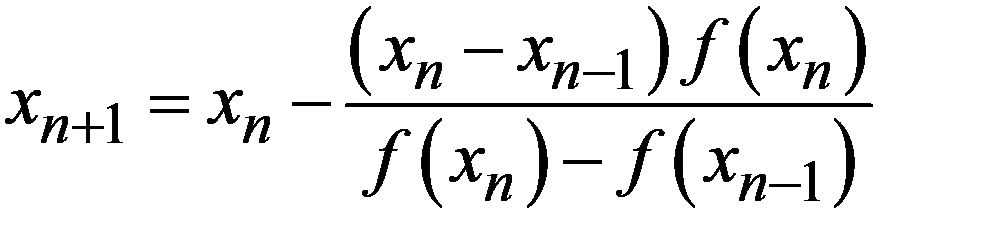 по формуле Тейлора с центром в точке
по формуле Тейлора с центром в точке 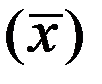 . Получим с точностью до бесконечно малых более высокого порядка
. Получим с точностью до бесконечно малых более высокого порядка 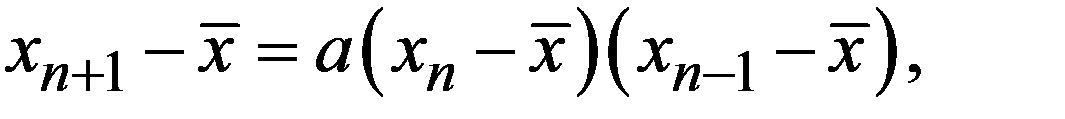
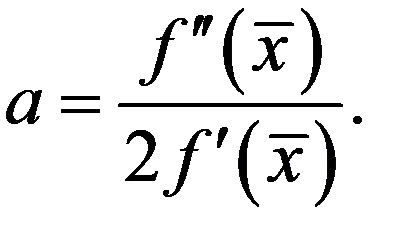 (17.2) Решение этого рекуррентного соотношения естественно искать в виде
(17.2) Решение этого рекуррентного соотношения естественно искать в виде
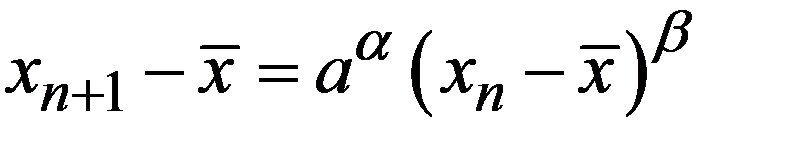 .
.
Подставляя эту формулу в соотношение (17.2), получим:
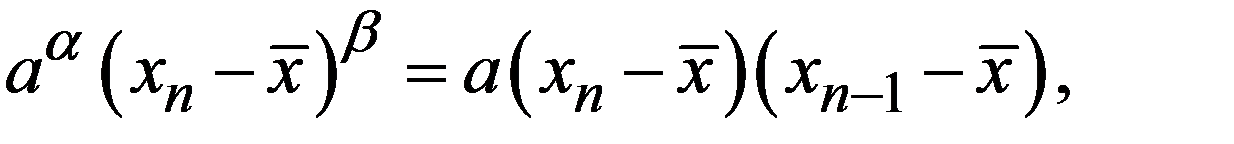
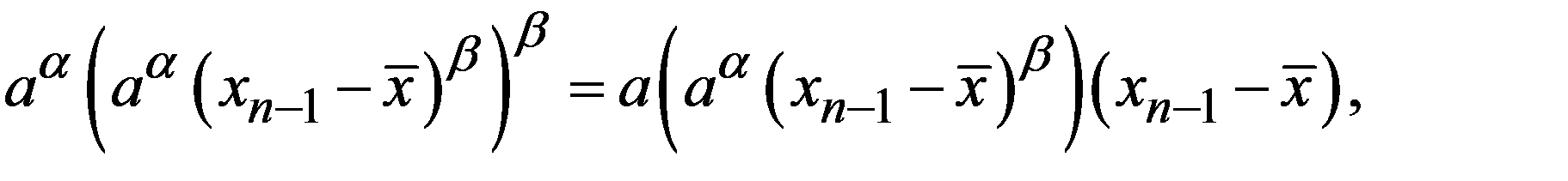
 .
.
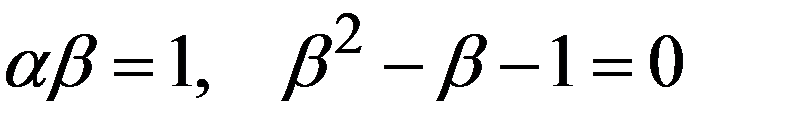 .
.
Только положительный корень  квадратного уравнения
квадратного уравнения 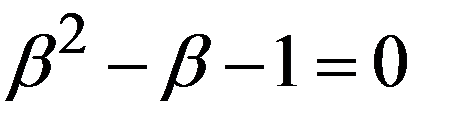
соответствует убыванию ошибки, т.е. сходящемуся процессу. Следовательно, в методе секущих
 ,
,
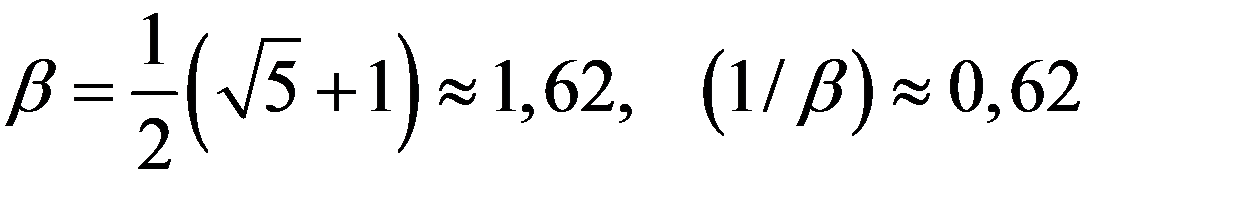 ,
,
в то время как в методе Ньютона ошибка убывает быстрей (соответствуя  =2). Но в методе Ньютона на каждой итерации надо вычислять и функцию, и производную, а в методе секущих – только функцию. Поэтому при одинаковом объеме вычислений в методе секущих можно сделать вдвое больше итераций и получить более высокую точность.
=2). Но в методе Ньютона на каждой итерации надо вычислять и функцию, и производную, а в методе секущих – только функцию. Поэтому при одинаковом объеме вычислений в методе секущих можно сделать вдвое больше итераций и получить более высокую точность.
В знаменателе формулы стоит разность значений функций. Вдали от корня это несущественно; но вблизи корня, особенно корня высокой кратности, значения функции малы и очень близки. Возникает потеря значащих цифр, приводящая к «разболтке» счета. Это ограничивает точность, с которой можно найти корень; для простых корней это ограничение невелико, а для кратных может быть существенным.
От «разболтки» страхуются так называемым приемом Гарвика. Выбирают не очень малое 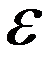 , ведут итерации до выполнения условия
, ведут итерации до выполнения условия 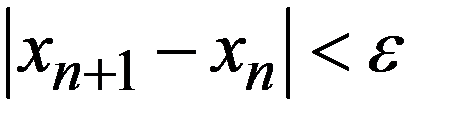 и затем продолжают расчет до тех пор, пока
и затем продолжают расчет до тех пор, пока 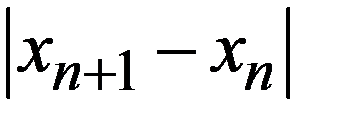 убывают. Первое же возрастание обычно означает начало «разболтки»; тогда расчет прекращают и последнюю итерацию не используют.
убывают. Первое же возрастание обычно означает начало «разболтки»; тогда расчет прекращают и последнюю итерацию не используют.
Метод парабол
Метод секущих можно рассматривать как замену функции f (x) интерполяционным многочленом первой степени, проведенным по узлам 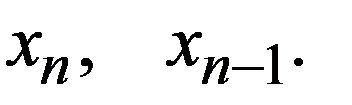 По трем последним итерациям можно построить интерполяционный многочлен второй степени, т.е. заменить график функции параболой. Запишем интерполяционный многочлен в форме Ньютона
По трем последним итерациям можно построить интерполяционный многочлен второй степени, т.е. заменить график функции параболой. Запишем интерполяционный многочлен в форме Ньютона
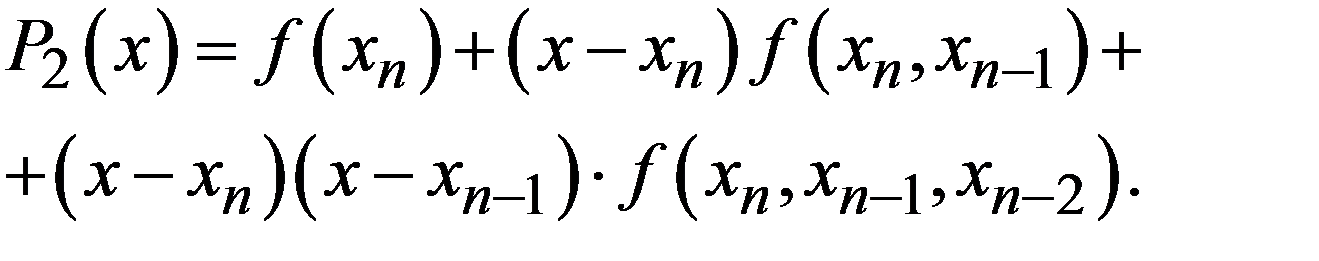
Приравнивая его нулю, получим квадратное уравнение
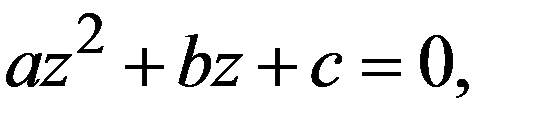 (17.3)
(17.3)
где 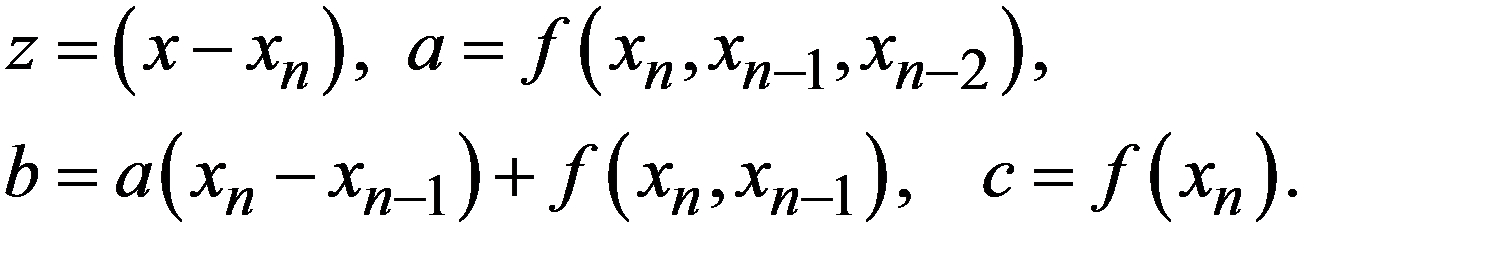
Тот из двух корней квадратного уравнения (17.3), который меньше по модулю, определяет новое приближение 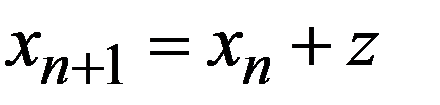 .
.
Очевидно, для начала расчета надо задать три первых приближения 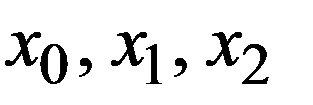 (обычно наугад выбирают три числа), т.е. процесс является трехшаговым.
(обычно наугад выбирают три числа), т.е. процесс является трехшаговым.
Метод парабол построен по образцу методов третьего порядка. Однако замена производных разделенными разностями приводит к существенному уменьшению скорости сходимости. Можно показать, что вблизи простого корня выполняется соотношение
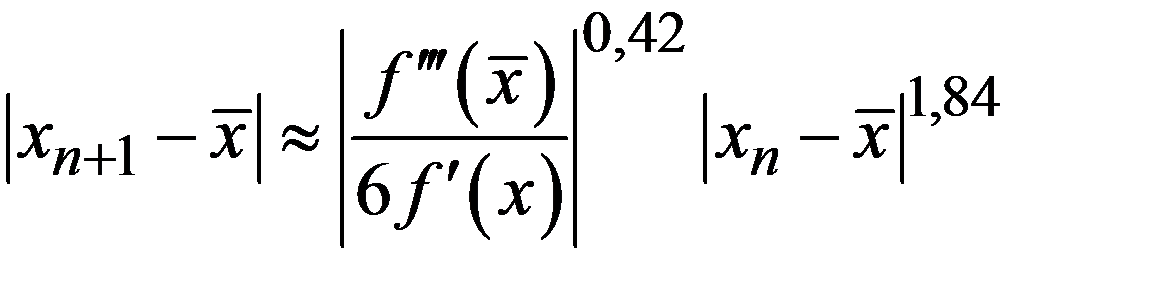 ,
,
т.е. сходимость даже медленнее квадратичной сходимости. Вблизи кратного корня сходимость еще медленнее (хотя и более быстрая, чем линейная). Заметим, что строить аналогичные методы с использованием интерполяционного многочлена еще более высокой степени невыгодно: сходимость все равно будет медленней квадратичной, а расчет сильно усложняется.
В методе парабол «разболтка» счета вблизи корня сказывается еще сильней, чем в методе секущих, ибо в расчете участвуют вторые разности. Тем не менее, корни можно найти с хорошей точностью; для определения оптимального числа итераций удобно пользоваться приемом Гарвика.
Метод парабол имеет важное достоинство. Даже если все предыдущие приближения действительны, уравнение (16.5) может привести к комплексным числам. Поэтому процесс может естественно сойтись к комплексному корню исходного уравнения. В методах простых итераций, касательных или секущих для сходимости к комплексному корню может потребоваться задание комплексного начального приближения, если f (x) вещественна при вещественном аргументе.
Корни многочлена
Метод парабол оказался исключительно эффективным для нахождения всех корней многочлена высокой степени. Если f (x) – алгебраический многочлен, то, хотя сходимость метода при произвольном начальном приближении и не доказана, на практике итерации всегда сходятся к какому-нибудь корню, причем быстро. Для многочлена частное 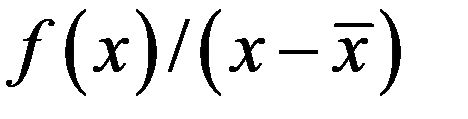 есть тоже многочлен, поэтому, последовательно удаляя найденные корни, можно найти все корни исходного многочлена.
есть тоже многочлен, поэтому, последовательно удаляя найденные корни, можно найти все корни исходного многочлена.
Замечание 1. Если f (x) – многочлен высокой степени, то возникают дополнительные трудности. Многочлен быстро возрастает при увеличении аргумента, поэтому в программе для ЭВМ должна быть страховка от переполнения. Обычно вводят масштабные множители, величина которых связана с диапазоном изменения аргумента.
Замечание 2. Для удаления вычисленных корней надо делить многочлен. Это вносит погрешность округления в коэффициенты и влияет на точность нахождения следующих корней. На практике отмечено, что если сначала удалять меньшие по модулю корни, точность падает мало, но если начать удаление с больших корней, точность может упасть катастрофически. Поэтому за начальное приближение берут 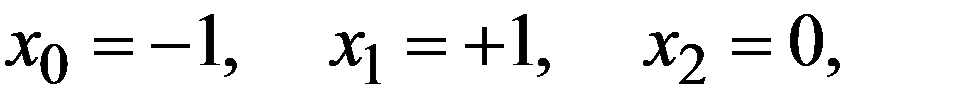 тогда итерации, обычно, сходятся к наименьшему по модулю корню. Его удаляют и по такому же начальному приближению ищут следующий корень и т.д. При такой организации вычислений потеря точности будет небольшой.
тогда итерации, обычно, сходятся к наименьшему по модулю корню. Его удаляют и по такому же начальному приближению ищут следующий корень и т.д. При такой организации вычислений потеря точности будет небольшой.