Для более подробного анализа возмущений среды, создаваемых точечным источником, рассмотрим решение системы уравнений, исключив из нее одну из неизвестных, например, скорость. При этом удобно перейти к волновому уравнению второго порядка. Наличие точечного источника возмущения плотности описывается введением -функции в правой части уравнения.
Пусть среда, в которой находится источник, движется со скоростью V в положительном направлении оси OX. Размеры источника будем считать пренебрежимо малыми, а его воздействие на среду – периодическим. В этом случае волновое уравнение будет неоднородным. Пусть возмущение среды описывается скалярной функцией j:
.
Решение уравнения удобно проводить с помощью разложения Фурье по плоским волнам:
, 
,
что дает для временной зависимости фурье-компоненты уравнение вынужденных колебаний вида
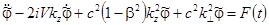, (1)
с правой частью
.
Решение уравнения вынужденных колебаний мы будем проводить с помощью функции Грина, что позволяет в явном виде учесть условие причинности. Будем искать это решение в виде
. (2)
Интегрирование по времени формально можно вести до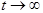 
, если положить, что функция Грина имеет вид:
.
Такое представление функции Грина соответствует обычному представлению о последовательности причинно-следственных связях, когда динамическая переменная не может зависеть от будущего воздействия на систему.
Подставляя решение (2) в уравнение (1), для функции Грина получим уравнение:
, (3)
откуда следует, что выражение в фигурных скобках является d-функцией:
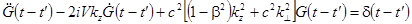. (4)
Фурье-образ для функции Грина 
, который мы определим выражением
формально выражается дробью
,
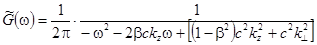знаменатель которой обращается в нуль в точках 
, где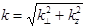 
- волновое число. Для определения функции Грина 
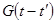следует вычислить интеграл, что удобно сделать с помощью теории вычетов. При этом можно так выбрать контур интегрирования, что условие причинности будет выполнено автоматически. Для этого достаточно обойти полюса сверху в комплексной плоскости w или, что тоже самое, сместить оба полюса вниз с действительной оси на малую величину 
, которую после вычисления интеграла следует устремить к нулю.
.
Вычисляя интеграл при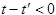 
по контуру, который замыкается в верхней полуплоскости, мы получим нуль, так как внутри контура полюсов нет. При 
контур следует замыкать в нижней полуплоскости, где расположены полюса. Это приводит к следующему выражению:
.
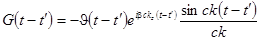Зависимость от времени фурье-компоненты плоской волны имеет вид:
Теперь нетрудно получить выражение для пространственного распределения поля, создаваемого точечным источником:
Внутренний интеграл представим в виде:
, где 
.
Для выполнения интегрирования выберем сферическую систему так, чтобы полярный угол J отсчитывался от вектора 
. Тогда
.
Для запаздывающей функции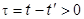 
, 
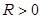, так что 
и
.
Фаза зависит от запаздывающего времени, обусловленное конечным временем распространения возмущения.
.
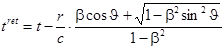Поверхности равной фазы, определяющие волновой фронт в некоторый момент времени, изображены на рисунке.
При движении потока со скоростью, превышающей скорость звука (в неподвижном газе), область возмущения имеет вид конуса, угол раствора которого называется углом Маха и определяется выражением: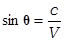 
.
Рис.