Общая теория
Определение 1. Уравнение, в которое входят независимая переменная (независимые переменные), искомая функция и ее производные называется дифференциальным.
Выделяют два класса дифференциальных уравнений – обыкновенные дифференциальные уравнения, если искомая функция зависит от одной переменной, и уравнения в частных производных, когда искомая функция является функцией многих переменных.
В данном разделе рассматриваются только обыкновенные дифференциальные уравнения, их в дальнейшем будем называть "дифференциальными уравнениями".
Определение 2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Определение 3. Решением (интегралом) дифференциального уравнения называют любую функцию, обращающую уравнение в тождество.
Процедура нахождения искомой функции из дифференциального уравнения называется его решением или интегрированием.
Для этого необходимо "избавиться" от входящих в уравнение производных, что возможно, как известно, только с помощью интегрирования, то есть вычисления неопределенных интегралов. При решении уравнения первого порядка, необходимо одно интегрирование, уравнение второго порядка следует интегрировать дважды и так далее. Но при каждом интегрировании, то есть вычислении неопределенного интеграла, появляется постоянная интегрирования. Следовательно, в решение уравнения 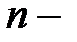 го порядка может входить
го порядка может входить 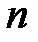 постоянных интегрирования. Другими словами, решений каждого дифференциального уравнения бесчисленное множество, отличаются они значениями постоянных интегрирования.
постоянных интегрирования. Другими словами, решений каждого дифференциального уравнения бесчисленное множество, отличаются они значениями постоянных интегрирования.
Выделяют два вида решений дифференциального уравнения. Частное его решение, представляющее в соответствии с определением 3 любую функцию, обращающую уравнение в тождество. И общее решение - множество всех частных решений данного уравнения. Частное решение может содержать, или не содержать, постоянные интегрирования. В общем решении число постоянных интегрирования должно совпадать с порядком уравнения.
Пример. 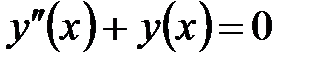 . Легко проверить, что частным решением этого уравнения является функция
. Легко проверить, что частным решением этого уравнения является функция 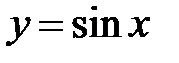 . Другое частное решение
. Другое частное решение 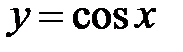 . Можно показать, что общее его решение имеет вид
. Можно показать, что общее его решение имеет вид 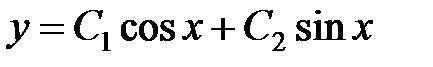 , где
, где 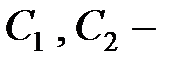 постоянные интегрирования.
постоянные интегрирования.
Определение 4. Задача Коши кроме дифференциального уравнения 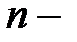 го порядка
го порядка 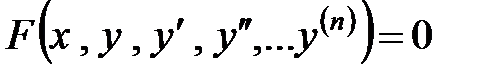 содержит
содержит 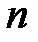 дополнительных условий, задаваемых в одной точке(при одном значении независимой переменной), то есть в точке
дополнительных условий, задаваемых в одной точке(при одном значении независимой переменной), то есть в точке 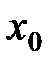 задается значение искомой функции
задается значение искомой функции 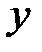 и ее производных до
и ее производных до 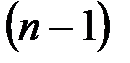 порядка. Часто эти условия называют начальными условиями задачи.
порядка. Часто эти условия называют начальными условиями задачи.
Физически решение задачи Коши можно представить следующим образом. Задается информация об исследуемом явлении в некоторый (начальный) момент, с помощью решения дифференциального уравнения определяется развитие этого явления в последующем.
Определение 5. Краевой (граничной) задачей для дифференциального уравнения называют задачу, в которой дополнительные условия задаются в более чем одной точке (на границах некоторого отрезка, на линиях или поверхностях для уравнений в частных производных). Дополнительные условия в этом случае называют краевыми или граничными условиями задачи. Общее число краевых условий, естественно, должно совпадать с порядком уравнения (числом постоянных интегрирования в общем решении уравнения).
В отличие от задачи Коши, в краевой задаче задается информация о поведении искомой функции на границе некоторой области, решение дифференциального уравнения позволяет определить эту функцию внутри заданной области, или вне ее.
Поскольку дополнительные условия задачи Коши или краевой задачи позволяют определить конкретные значения всех постоянных интегрирования, входящих в общее решение уравнения, решения этих задач являются частными решениями дифференциального уравнения.
Определение 6. Математическая модель – это математическое описание какого-то процесса или явления.
Современные математические модели, как правило, содержат дифференциальные или более сложные уравнения и соответствующее число дополнительных условий. Чтобы исследовать развитие изучаемого процесса или явления, необходимо это уравнение решить. Решения могут быть точными и приближенными (чаще всего численными).
Построим математическую модель полета снаряда. Из второго закона Ньютона следует 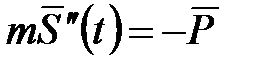 . Здесь P – вес снаряда,
. Здесь P – вес снаряда, 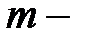 его масса,
его масса, 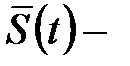 вектор пути, пролетаемого снарядом,
вектор пути, пролетаемого снарядом, 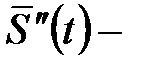 ускорение снаряда, t –время. Дополнительные условия: известно местоположение орудия
ускорение снаряда, t –время. Дополнительные условия: известно местоположение орудия 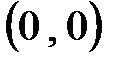 и начальная скорость снаряда
и начальная скорость снаряда 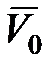 , создаваема зарядом.Вектор нача0льной скорости (дуло орудия) направлен под углом
, создаваема зарядом.Вектор нача0льной скорости (дуло орудия) направлен под углом 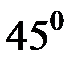 к горизонтальной оси x. Поскольку вес снаряда
к горизонтальной оси x. Поскольку вес снаряда 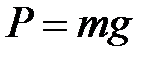 , g–ускорение свободного падения тела, построена задача Коши. Если
, g–ускорение свободного падения тела, построена задача Коши. Если 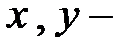 проекции вектора пути
проекции вектора пути 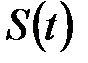 на оси координат, то векторное уравнение закона Ньютона после сокращения на массу приводит к системе уравнений
на оси координат, то векторное уравнение закона Ньютона после сокращения на массу приводит к системе уравнений 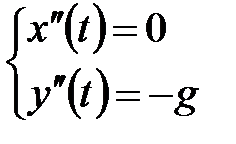 с дополнительнымиусловиям
с дополнительнымиусловиям 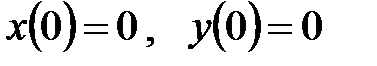 ,
, 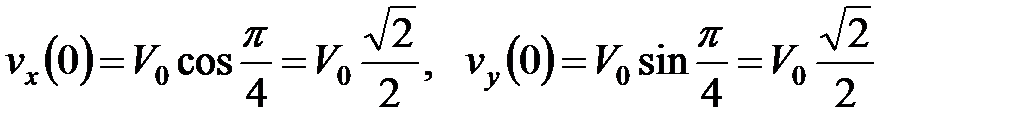 .
.
Система уравнений приводится к виду  , здесь
, здесь 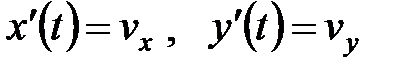 . Решаем первое уравнение: из
. Решаем первое уравнение: из 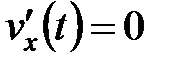 следует
следует 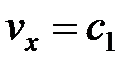 ,
,
(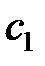 - постоянная). Интегрируем второе уравнение
- постоянная). Интегрируем второе уравнение 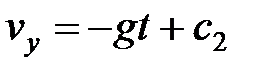 . Поскольку
. Поскольку
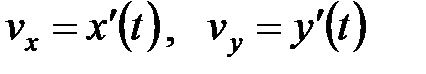 , получаем еще пару уравнений
, получаем еще пару уравнений 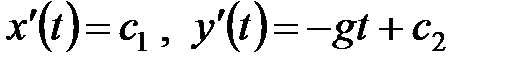 .
.
Интегрируя их, получаем 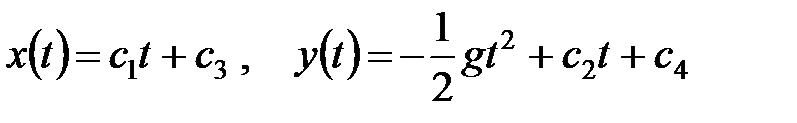 . Итак, решение системы уравнений построено. Остается определить значения постоянных интегрирования. Выполняем дополнительные (начальные) условия
. Итак, решение системы уравнений построено. Остается определить значения постоянных интегрирования. Выполняем дополнительные (начальные) условия
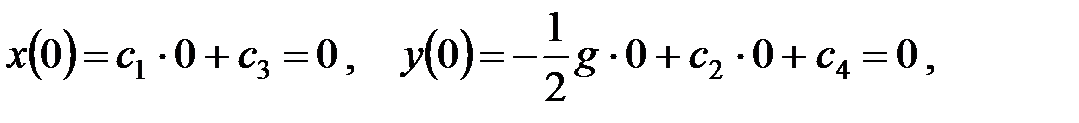
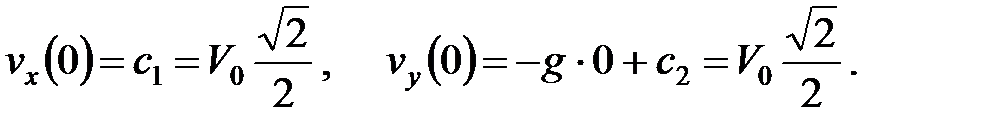
Из решения полученной системы имеем
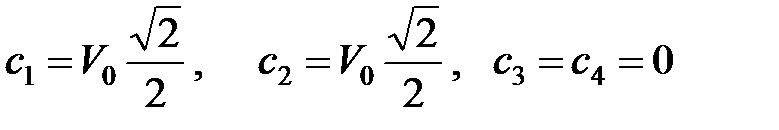 .
.
Построено параметрическое уравнение траектории движения снаряда
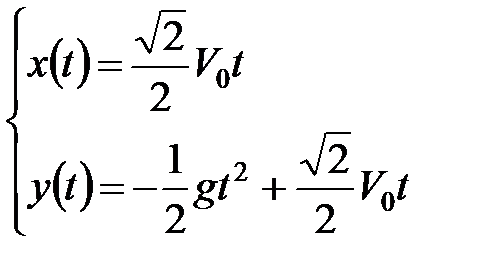 .
.
Определим вид кривой, исключив время t.
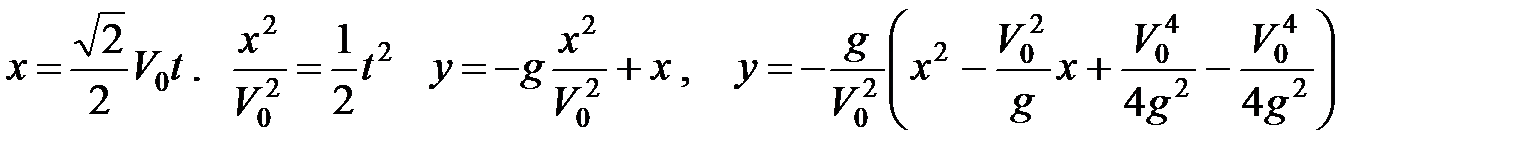 /
/
Ее каноническое уравнение
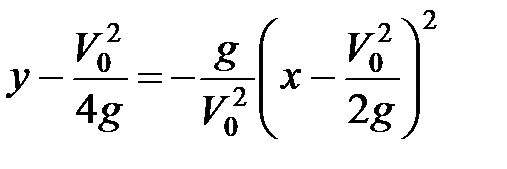 .
.
Имея уравнение траектории снаряда, можем определить время полета и дальность выстрела:
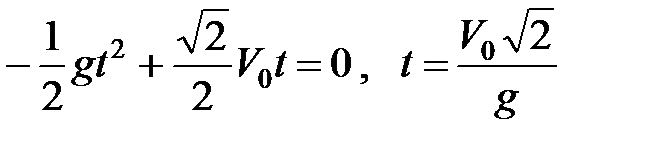 ,
, 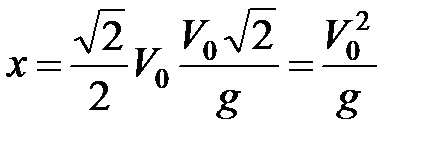 .
.
В качестве примера была выбрана система простейших дифференциальных уравнений. Современные математические модели более сложных процессов и явлений приводят к значительно более сложным дифференциальным уравнениям, решению которых посвящено множество научных статей и монографий.
Простейшие дифференциальные уравнения первого порядка
Уравнения с разделяющимися переменными
Уравнения вида
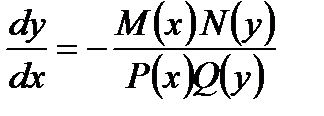 (1)
(1)
называются уравнениями с разделяющимися переменными. Их интегрирование осуществляется с помощью разделения переменных, то есть приведения уравнения к виду
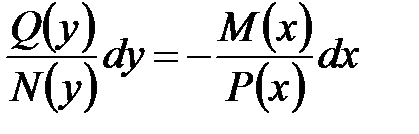 , (2)
, (2)
то есть к уравнению с разделенными переменными. Эта процедура законна только при 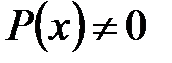 и
и 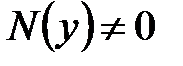 . Следовательно, при переходе от уравнения с разделяющимися переменными (1) к уравнению с разделенными переменными (2) могут быть потеряны решения уравнения (5) вида
. Следовательно, при переходе от уравнения с разделяющимися переменными (1) к уравнению с разделенными переменными (2) могут быть потеряны решения уравнения (5) вида 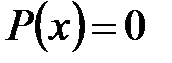 и
и 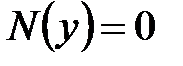 , если они существуют.
, если они существуют.
Переход от уравнения (2) к его решению

можно формально обосновать следующим образом. Уравнение (2) представляет собой равенство двух функций. Но если две функции равны, то их первообразные 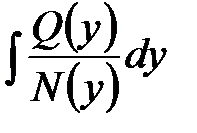 и
и 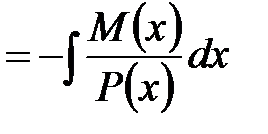 отличаются на постоянную.
отличаются на постоянную.
Пример 1. Решить уравнение 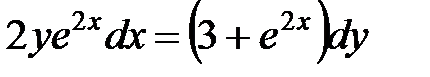 .
.
Разделяем переменные, поделив обе части уравнения на 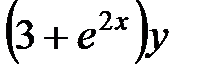 ,
,
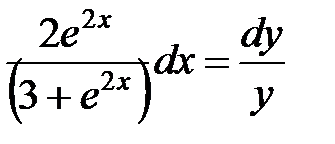 .
.
Так как 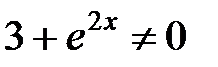 , в результате деления может быть потеряно только решение
, в результате деления может быть потеряно только решение 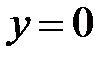 . Оно, действительно, является решением исходного уравнения поскольку
. Оно, действительно, является решением исходного уравнения поскольку 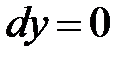 .
.
Интегрируем уравнение с разделенными переменными
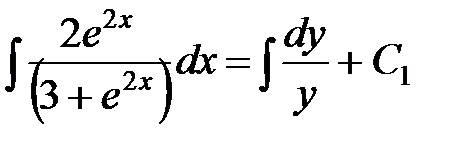 ,
,
откуда следует
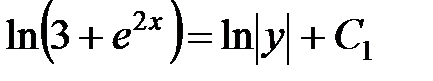 .
.
Обозначим постоянную интегрирования 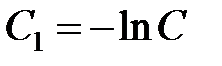 и избавимся от логарифмов, тогда
и избавимся от логарифмов, тогда 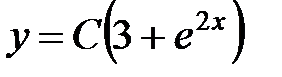 . Отметим, что " потерянное" решение в данном случае входит в общее решение уравнения (при
. Отметим, что " потерянное" решение в данном случае входит в общее решение уравнения (при 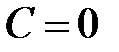 ). Ответ
). Ответ 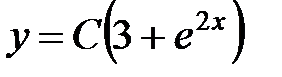 .
.
Отметим, что в этом примере найдено общее решение дифференциального уравнения.
Пример 2. Решить задачу Коши
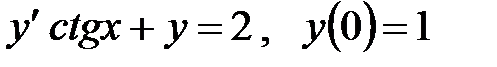 .
.
Разделяем переменные с помощью следующих процедур
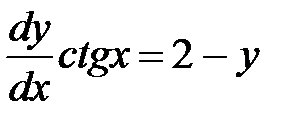
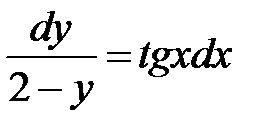
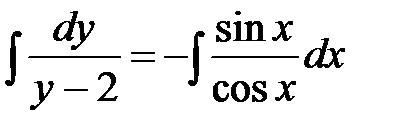
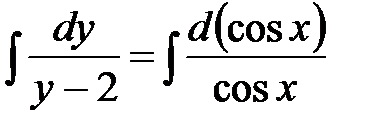 .
.
Интегрируя, находим общее решение уравнения
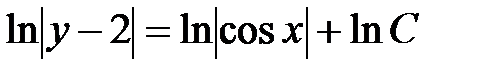 .
.
В итоге 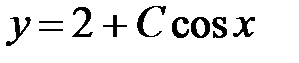 . Из начального условия определяем значение постоянной интегрирования. Из
. Из начального условия определяем значение постоянной интегрирования. Из 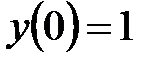 имеем
имеем 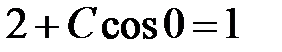 и
и 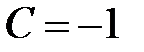 . Решение задачи Коши
. Решение задачи Коши 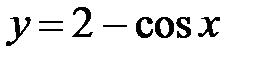 .
.
Проверка. 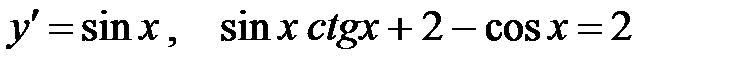 . Следовательно, найденная функция является решением уравнения. Она удовлетворяет и начальному условию
. Следовательно, найденная функция является решением уравнения. Она удовлетворяет и начальному условию 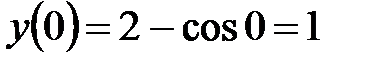 .
.
Пример 3. Решить уравнение 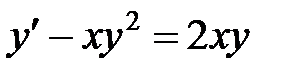 .
.
Разделяем переменные
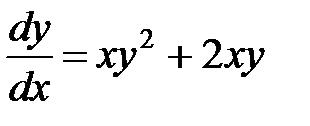 ,
, 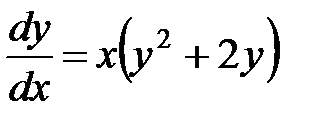 ,
, 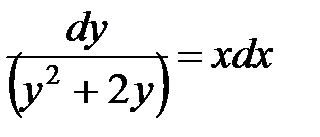 ,
, 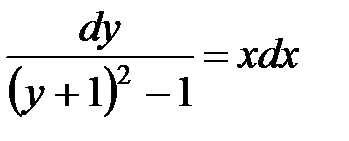 .
.
При разделении переменных обе части уравнения нужно было поделить на выражение 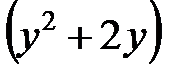 , то есть могли быть потеряны решения
, то есть могли быть потеряны решения 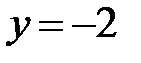 и
и 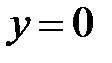 . Проверим, являются ли эти функции решением исходного уравнения. Если
. Проверим, являются ли эти функции решением исходного уравнения. Если 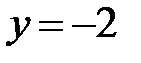 , то
, то 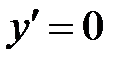 , и уравнение тождественно выполняется. При
, и уравнение тождественно выполняется. При 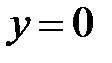 также
также 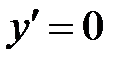 , и уравнение превращается в тождество. Следовательно,
, и уравнение превращается в тождество. Следовательно, 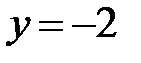 и
и 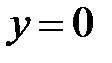 являются решениями исходного уравнения.
являются решениями исходного уравнения.
В результате интегрирования уравнения с разделенными переменными получаем
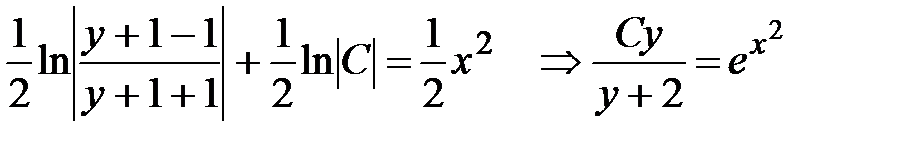 , откуда следует
, откуда следует 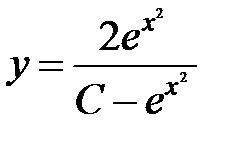
Нетрудно заметить, что 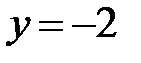 входит в общее решение уравнения и реализуется при
входит в общее решение уравнения и реализуется при 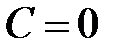 . Функция
. Функция 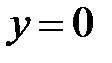 не входит в общее решение уравнения, следовательно, является особым решением.
не входит в общее решение уравнения, следовательно, является особым решением.
Ответ 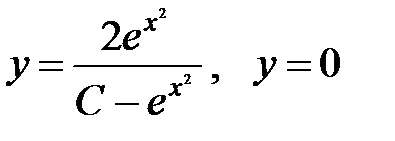 .
.
Однородные дифференциальные уравнения первого порядка
Определение 1. Функция 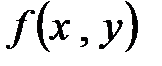 называется однородной функцией степени
называется однородной функцией степени  , если при любом
, если при любом 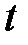 имеет место тождество
имеет место тождество 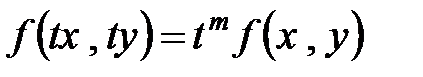 .
.
Определение 2. Уравнение 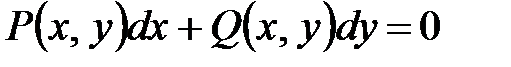 называется однородным, если функции
называется однородным, если функции 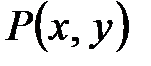 и
и 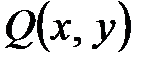 являются однородными функциями одного порядка.
являются однородными функциями одного порядка.
Следствие. Уравнение 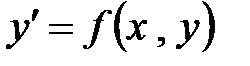 однородное, если функция
однородное, если функция 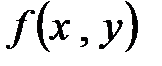 - однородная функция нулевого порядка, то есть
- однородная функция нулевого порядка, то есть 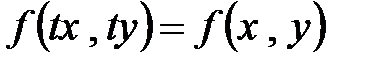 .
.
Однородное уравнение первого порядка сводится к уравнению с разделяющимися переменными при помощи замены искомой функции 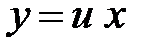 . Покажем это. Пусть
. Покажем это. Пусть 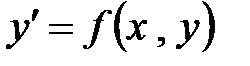 . Поскольку
. Поскольку 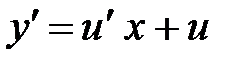 , решаемое уравнение принимает вид
, решаемое уравнение принимает вид 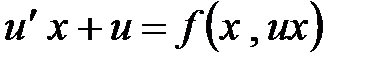 . В силу однородности функции
. В силу однородности функции 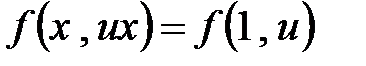 , В результате
, В результате
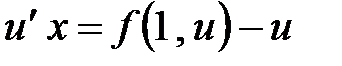 ,
, 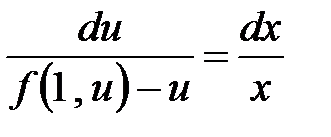 ,
, 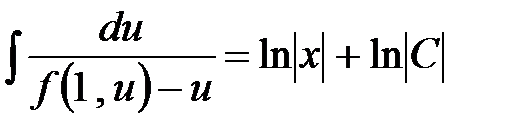 .
.
Вычисляя интеграл в левой части уравнения и возвращаясь к функции 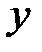 , получаем общее решение уравнения.
, получаем общее решение уравнения.
Пример 1. 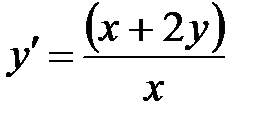 .
.
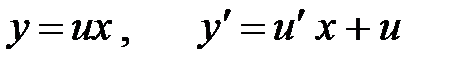 , тогда
, тогда 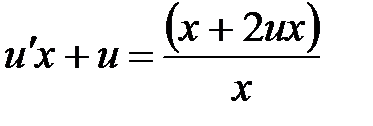 ,
, 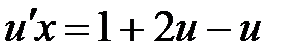 ,
, 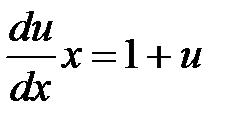 .
.
Для разделения переменных необходимо поделить обе части уравненияна 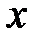 и
и 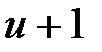 , следовательно, считать
, следовательно, считать 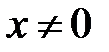 и
и 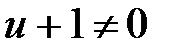 , при этом могут быть потеряны некоторые решения. В данном примере
, при этом могут быть потеряны некоторые решения. В данном примере 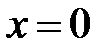 не является решением уравнения, а
не является решением уравнения, а 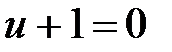 есть решение
есть решение 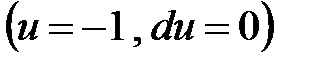 , то есть может быть потеряно решение уравнения
, то есть может быть потеряно решение уравнения 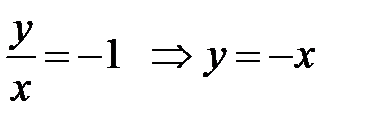 . Продолжаем решение уравнения, разделяя переменные
. Продолжаем решение уравнения, разделяя переменные
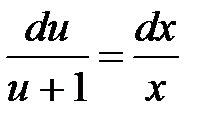 ,
, 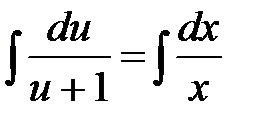 ,
, 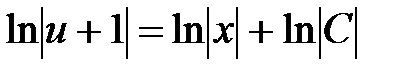 ,
, 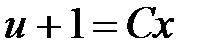 ,
, 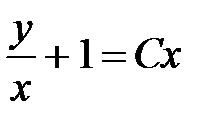 .
.
Ответ 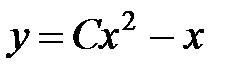 , причем "потерянное" решение входит в общее решение уравнения (при
, причем "потерянное" решение входит в общее решение уравнения (при 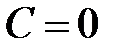 ).
).
Пример 2. 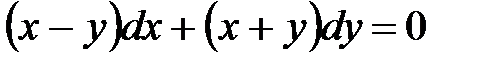 .
.
Пусть 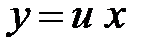 , тогда
, тогда 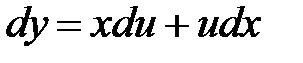 ,
, 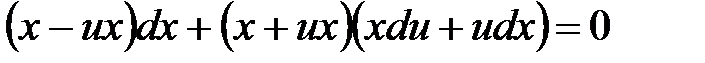 ,
,
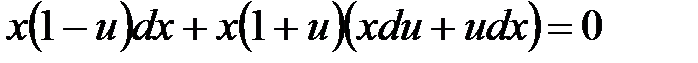 ,
, 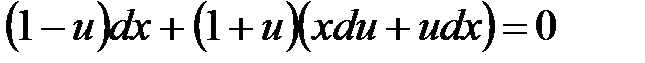 ,
,
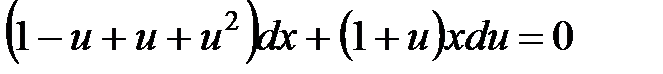 ,
, 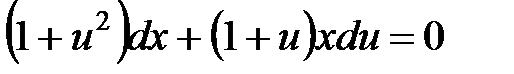 ,
,
Разделяем переменные
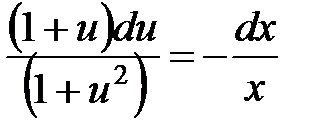 ,
, 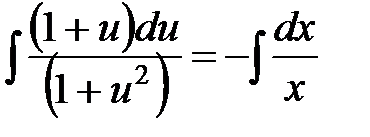 ,
, 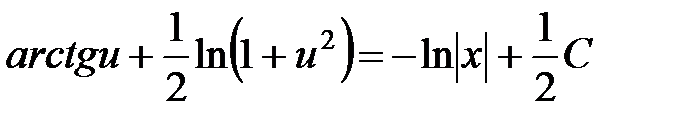 ,
,
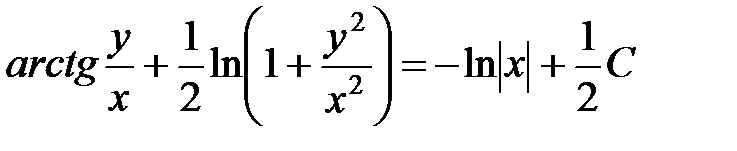 ,
, 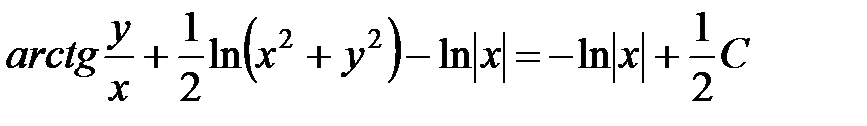 .
.
Ответ  .
.
Линейные дифференциальные уравнения первого порядка
Уравнение вида
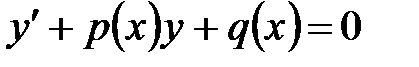 (3)
(3)
называется линейным дифференциальным уравнением первого порядка.
В линейном уравнении 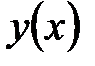 и ее производная
и ее производная 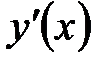 составляют линейную комбинацию, поскольку коэффициенты при них зависят только от
составляют линейную комбинацию, поскольку коэффициенты при них зависят только от 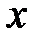 . Влинейной комбинации не может быть степеней функций
. Влинейной комбинации не может быть степеней функций 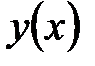 ,
, 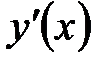 , кроме первой, нет произведения этих функций.
, кроме первой, нет произведения этих функций.
Линейные уравнения чаще всего встречаются в прикладных задачах, поэтому методов их решений несколько. Рассмотрим один из них, приводящий линейное уравнений первого порядка к двум уравнениям с разделяющимися переменными.
Решение уравнения (3) ищется в виде 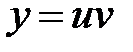 , то есть вместо одной искомой функции
, то есть вместо одной искомой функции 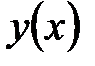 вводим две функции
вводим две функции 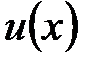 и
и 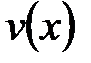 . Ясно, что
. Ясно, что 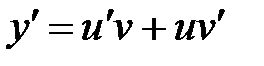 . Подставляем эти соотношения в уравнение
. Подставляем эти соотношения в уравнение
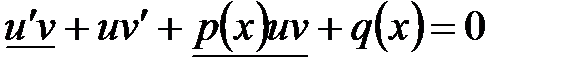
и группируем подчеркнутые члены уравнения (можно группировать и второй с третьим члены) 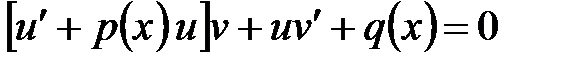 . Распорядимся функцией
. Распорядимся функцией 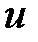 так, чтобы выражение в квадратных скобках равнялось нулю, тогда вместо одного уравнения получаем два
так, чтобы выражение в квадратных скобках равнялось нулю, тогда вместо одного уравнения получаем два 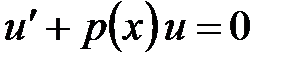 ,
, 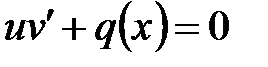 , одно относительно
, одно относительно  и второе относительно
и второе относительно  . Поскольку в ходе решения каждого уравнения появляется постоянная интегрирования, их оказывается две. Но общее решение уравнения (3) должно содержать одну произвольную постоянную, поэтому определяется любое частное решение первого уравнения (без постоянной интегрирования), а затем находится общее решение второго уравнения. Можно поступить по другому – определить общее решение первого уравнения и частное решение второго, но это не удобно, поскольку при определении
. Поскольку в ходе решения каждого уравнения появляется постоянная интегрирования, их оказывается две. Но общее решение уравнения (3) должно содержать одну произвольную постоянную, поэтому определяется любое частное решение первого уравнения (без постоянной интегрирования), а затем находится общее решение второго уравнения. Можно поступить по другому – определить общее решение первого уравнения и частное решение второго, но это не удобно, поскольку при определении 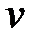 приходится интегрировать произвольную постоянную, и интегралы могут принимать значения, зависящие от знака этой произвольной постоянной, это приходится учитывать при получении окончательного результата.
приходится интегрировать произвольную постоянную, и интегралы могут принимать значения, зависящие от знака этой произвольной постоянной, это приходится учитывать при получении окончательного результата.
Итак,
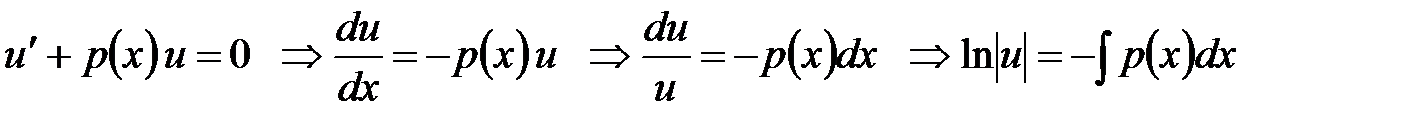 .
.
Откуда следует 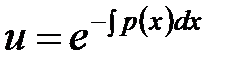 . Второе уравнение решаем с учетом найденной функции
. Второе уравнение решаем с учетом найденной функции 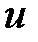 :
: 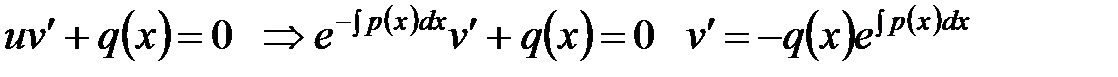 . Тогда
. Тогда 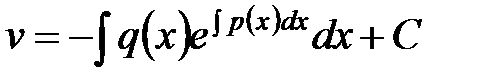 . Ответ.
. Ответ. 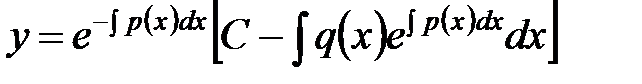 .
.
Пример 1. Определить общее решение уравнения 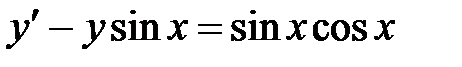 .
.
Пусть 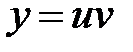 , тогда
, тогда 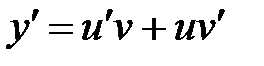 . Очевидно
. Очевидно
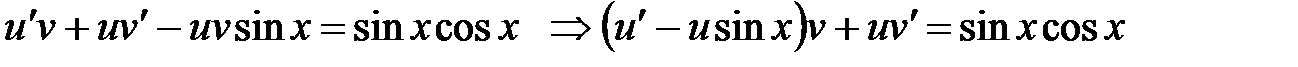 , откуда следует
, откуда следует
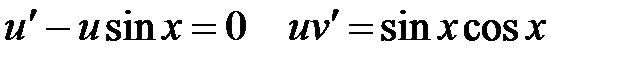 . Решаем первое уравнение
. Решаем первое уравнение
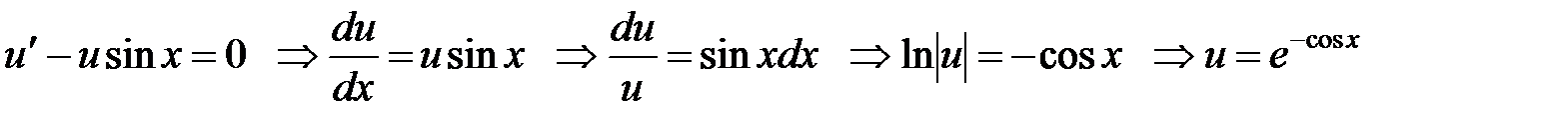 .
.
Теперь второе уравнение запишется следующим образом
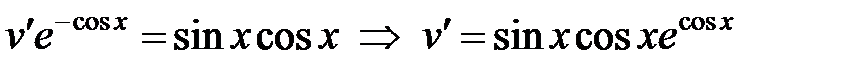 .
.
Отсюда имеем
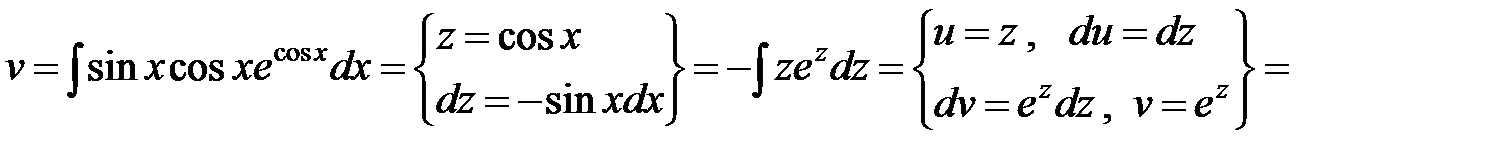
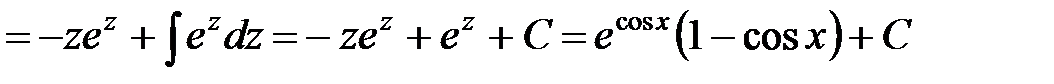 .
.
Очевидно 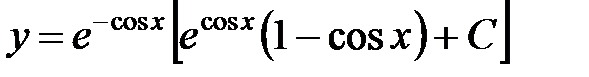 . Ответ
. Ответ 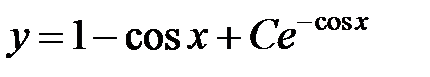 .
.
Проверка.
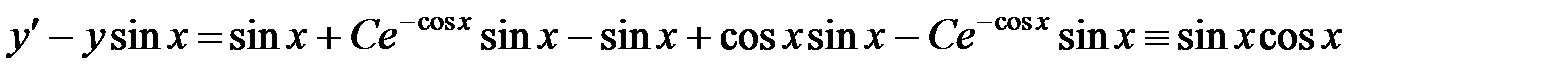 .
.
Уравнение выполняется тождественно.
Пример 2. Решить задачу Коши
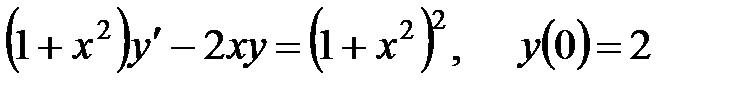 .
.
Определим вначале общее решение этого уравнения, затем из начального условия найдем значение постоянной интегрирования. Отметим, что уравнение можно привести к виду (3) делением на 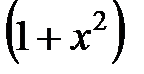 , но это делать не обязательно. Итак,
, но это делать не обязательно. Итак, 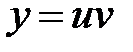 ,
, 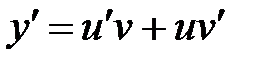 , тогда
, тогда
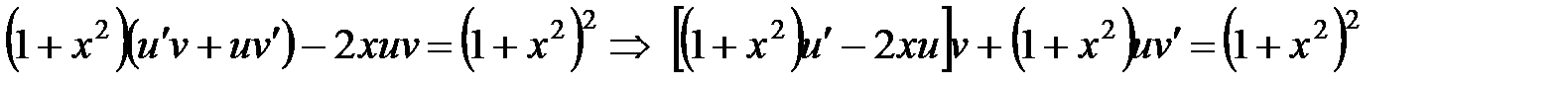 .
.
Решаем первое уравнение
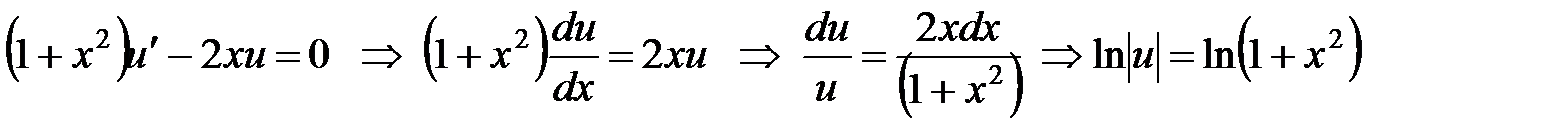 .
.
Очевидно, 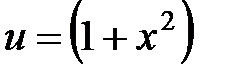 . Далее решаем второе уравнение
. Далее решаем второе уравнение 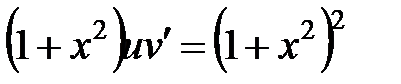 , из которого следует
, из которого следует 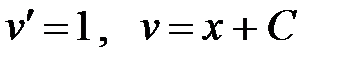 . Общее решение уравнения принимает вид
. Общее решение уравнения принимает вид 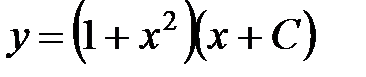 . Выполним начальное условие
. Выполним начальное условие 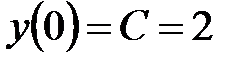 .
.
Ответ 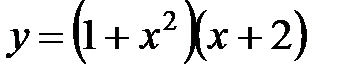 .
.
Проверка
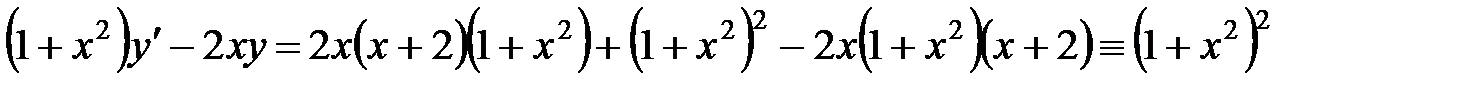 .
.