Как было показано выше токи в линейных электрических цепях, содержащих активные сопротивления, индуктивности и емкости, при питании этих цепей синусоидальным напряжением в установившемся режиме изменяются по закону синуса. Действующие или амплитудные значения этих токов и напряжений на отдельных участках цепи изображаются с помощью векторов на векторной диаграмме. Исследование и расчеты цепей основываются на применении законов Кирхгофа, приводивших к геометрическим действиям сложения и вычитания векторов токов и напряжений. С помощью векторных диаграмм можно производить и расчеты цепей, однако в случае сложных цепей эти расчеты были бы трудоемки и требовали бы большой точности в соблюдении масштабов диаграмм.
Развитие электроэнергетики и техники связи потребовало разработки инженерного аналитического метода расчета электрических цепей, позволяющего использовать уже хорошо известные приемы расчета сложных цепей постоянного тока. Таким методом расчета электрических цепей переменного тока явился символический метод или метод комплексных амплитуд. Символический метод является формальным переводом геометрических операций над векторами на язык алгебры комплексных чисел.
1. Представление векторов комплексными величинами. Метод векторных диаграмм дает ясное представление о взаимном соотношении изменяющихся величин, характеризующих явления переменного тока. Однако числовые расчеты при помощи этих диаграмм связаны иногда с очень большими погрешностями благодаря неточности графического построения, и в этом отношении аналитический способ имеет большое преимущество.
В векторных диаграммах каждый вектор, представляющий величину, изменяющуюся по закону синуса, вполне определяется двумя полярными координатами: длиной, которая может равняться или амплитуде, или действующему значению, и фазой или углом, который составляет этот вектор с некоторым другим вектором, принимаемым за исходный. Вместо употребления полярных координат можно определить этот вектор при помощи его проекций на две вполне определенные, взаимно перпендикулярные линии, например оси прямоугольных координат (рис. 3.29, а, б).
Так, вектор 
определяется через свои проекции: на горизонтальную ось 
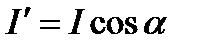и на вертикальную ось 
; 
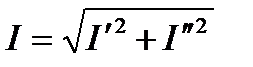. Вращение векторов принимается против часовой стрелки, и в этом отношении отсчет углов совпадает с направлением отсчета углов в системе прямолинейных координат на плоскости. Для того
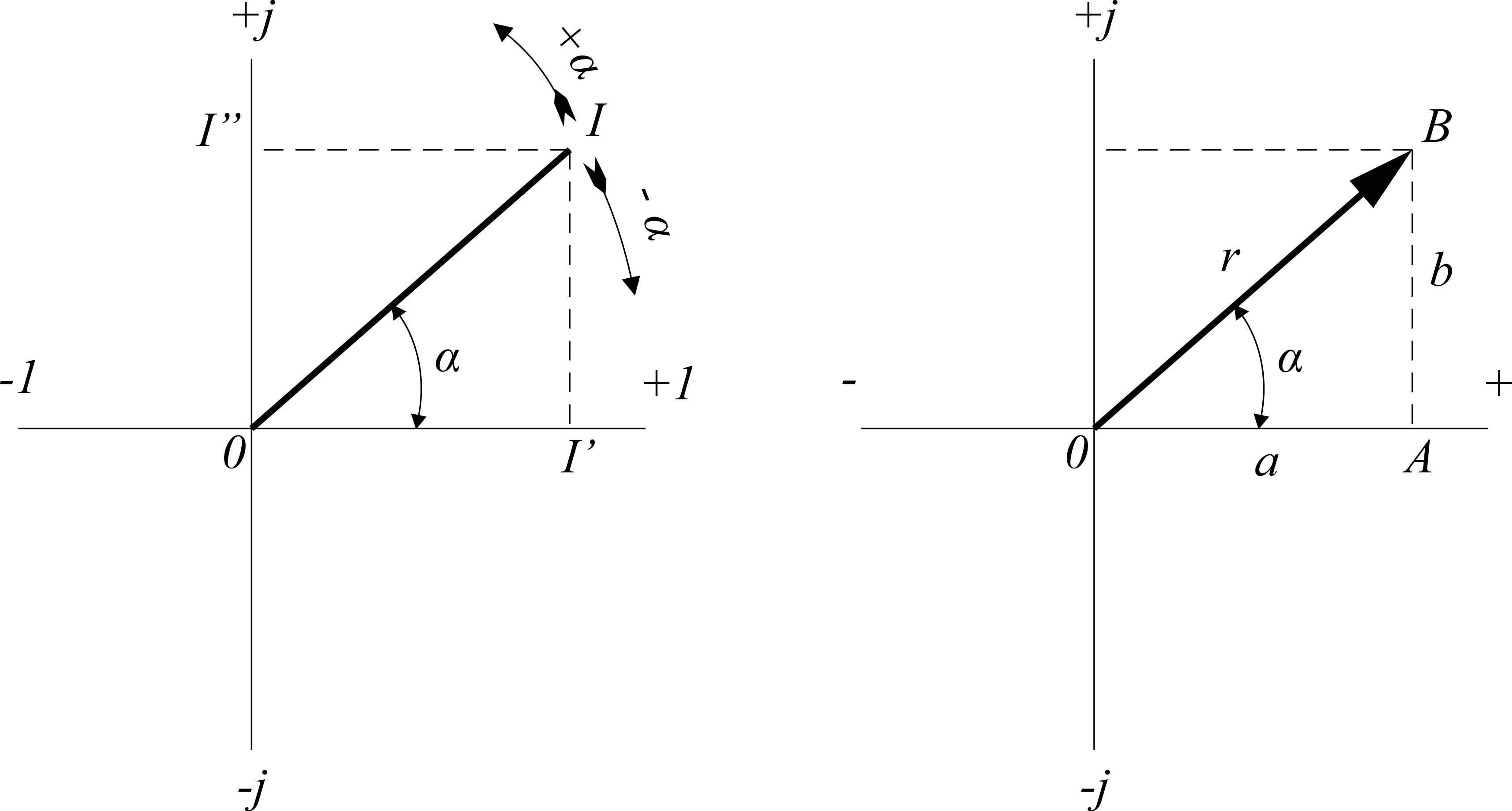Рис. 3.29 а и б. Геометрическое представление комплексов
|
и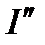 
, слагаемые по вертикальной оси снабжаются некоторым символическим показателем j. Тогда вектор 
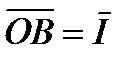можно выразить следующим образом:
.
Вторую часть написанного равенства нельзя рассматривать как простую сумму; символический знак j указывает, что вторая слагающая 
повернута по отношению к первой слагающей 
на 90 
в сторону вращения векторов. Согласно теории комплексов таким символическим коэффициентом служит мнимая единица: 
.
Из теории комплексных чисел известно, что:
1) 
;
; 
;
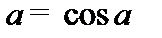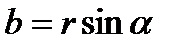здесь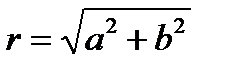 
- (модуль) и 
.
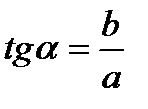Комплексы могут быть представлены геометрически (рис. 3.29, б), если по оси абсцисс откладывать действительные, а по оси ординат мнимые значения комплексов. Отрезки на обеих осях могут быть сложены геометрически: OB=r; 
.
2) Если два комплекса равны a+jb=a1+jb1, то a=a1 и b=b1, т.е. действительные и мнимые части равны в отдельности.
3) Всякий комплекс может быть представлен в трех формах записи:
,
где en– основание натуральных логарифмов.
4) 
, что следует из
;
,
кроме того
;
; 
.
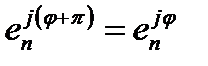5) Всякий комплекс может быть приведен к виду 
; например:
Или
,
где
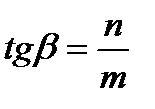и 
.
Равным образом
.
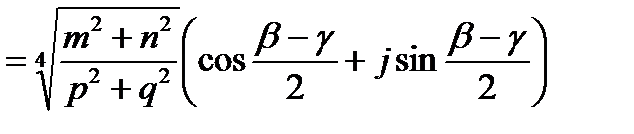Пользуясь комплексным методом, всякий вектор можно представить или проекциями на две взаимно перпендикулярные оси или же величиной этого вектора и углом, который этот вектор составляет с положительным направлением оси действительных значений
(рис. 3.29, а):
,
где
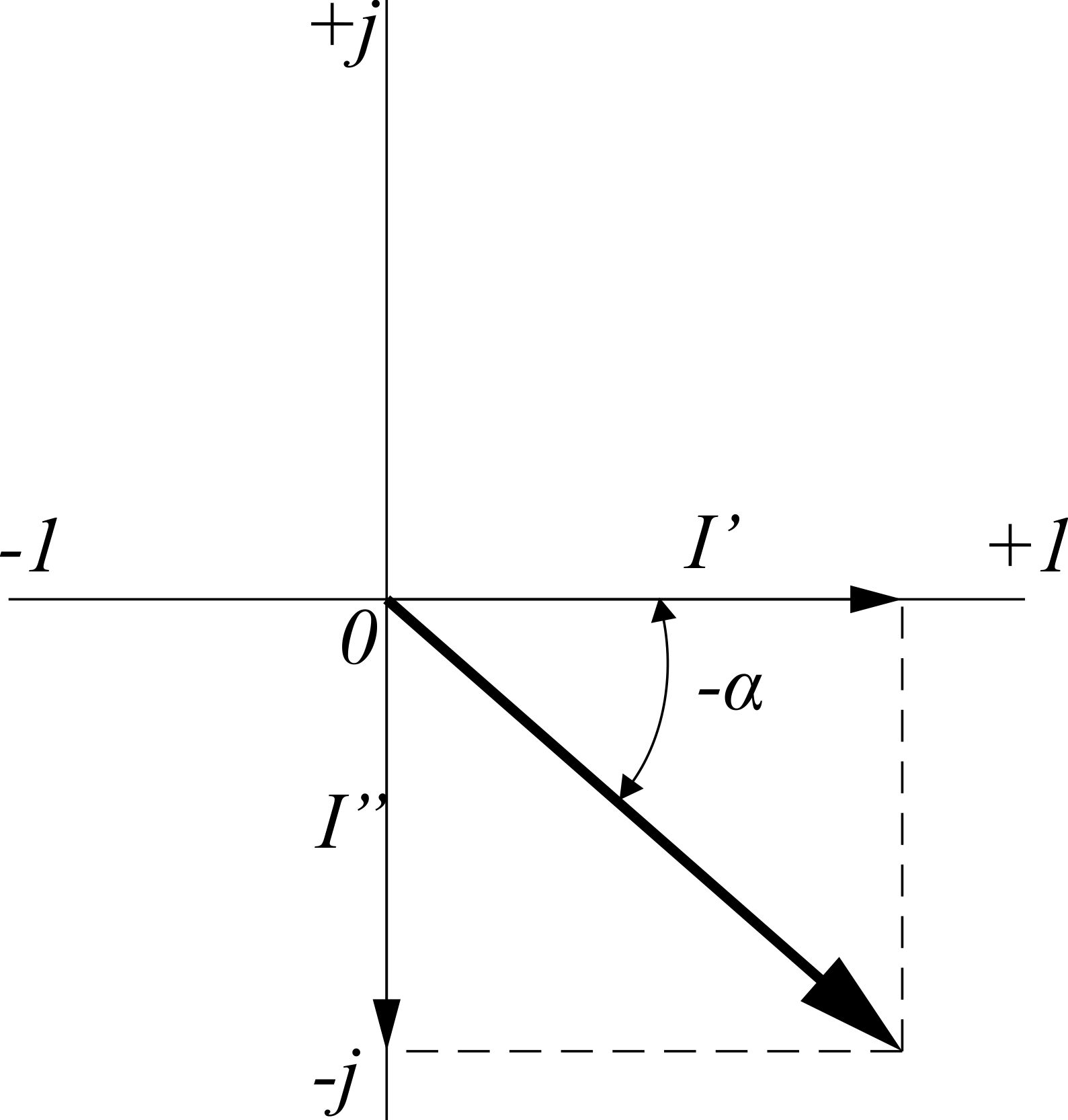Рис. 3.30. Геометрическое представление
тока
|
.
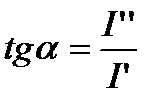Множитель 
указывает, что вектор 
повернут от некоторой оси на угол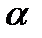 
по направлению обратному движению часовой стрелки.
Если вектор дан в виде 
, то это значит, что 
совпадает с положительным направлением оси абсцисс (рис. 3.30), а 
– с отрицательным направлением оси ординат:
.
Множитель 
указывает, что вектор 
повернут на угол a в сторону отрицательного счета углов (как это делается в аналитической геометрии), т.е. в сторону движения стрелки часов.
Если комплексное выражение данного вектора 
умножить на +j:
,
или
,
то это равносильно, повороту вектора на 90 в сторону вращения векторов. А умножение на –j:
.
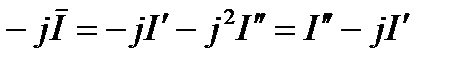или
будет соответствовать повороту вектора также на 90 , но в сторону, обратную вращению векторов.
Умножение вектора на (-I)=j2 можно рассматривать как двукратный поворот на 90 , т.е. всего на 180 :
Обозначая каждый вектор 
через его проекции на две взаимно перпендикулярные линии:
,
мы можем геометрическое сложение векторов заменить алгебраическим сложением комплексных выражений. Действительно, пусть даны три вектора:
.
2. Изображение гармонических величин в комплексной форме. Известно, что при исследовании явлений в цепях переменного тока для представления гармонических величин с неизменными амплитудами и постоянным числом периодов используются векторные диаграммы с определенным взаимным расположением векторов. Для нахождения мгновенных значений предполагается, что вся система векторов как жесткое целое вращается вокруг центра и проекции этих векторов на какую-нибудь вертикальную линию дают мгновенные значения переменных величин. Затем те же векторы для какого-нибудь момента как было выше показано, можно представить в виде комплексов слагающих по двум взаимно перпендикулярным осям, причем слагающие по одной оси считаются действительными величинами, а слагающие по другой имеют множитель 
.
Покажем теперь, как гармонические величины могут быть изображены при помощи мнимых степенных показателей.
Из математики известны соотношения (формулы Эйлера)
или 
.
Величины 
и 
можно рассматривать как единичные векторы, из которых первый повернут на угол 
в положительную сторону, т. е. против стрелки часов, а второй на тот же угол в противоположную сторону, т. е. по стрелке часов.
Выражение 
представляет полуразность этих двух векторов (рис. 3.31.) в векторной форме, т. е.
.
С другой стороны, отрезок СА по величине равен sinωt, а так как этот вектор направлен по оси +j, то мы можем написать;
.
С течением времени угол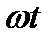 
будет увеличиваться и вместе с ним оба вектора 
и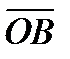 
будут поворачиваться на один и тот же угол относительно начальной линии O+. Вместо того чтобы брать каждый раз два вектора и находить их полуразность, мы можем ограничиться одним вектором 
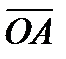,проектируя его непосредственно на ось +j, и через 
обозначить условно изменяющуюся по закону синуса величину.
Так как 
то, обозначая через 
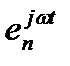гармонически изменяющуюся величину, мы должны условиться, что для нахождения мгновенного значения мы должны
| + |
| B |
| C |
| ωt |
| -ωt |
| -e-jωt |
| e jωt |
| A |
| +j |
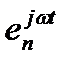разложить по формуле Муавра, и тогда величина, имеющая множитель j, представит и искомое мгновенное значение.
Если амплитуда гармонически изменяющейся величины не единица, а Аm,то функция Amsinωt может быть изображена через Am 
.
| Рис. 3.31. Геометрическое изображение гармонически изменяющихся величин |
, например Amsin(ωt+ 
), то мы такую величину опять-таки можем условно обозначить через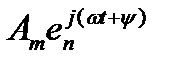 
, помня, что мгновенное значение будет равно после разложения в комплекс:
величине, имеющей перед собой множитель +j.
Указанный выше способ изображения переменных величин, изменяющихся по закону синуса, представляет во многих случаях большие удобства. Это удобство основано на том, что первая производная и интеграл по времени переменной синусоидальной величины находятся необыкновенно просто путем умножения и деления на некоторый условный множитель (оператор) 
.
Пусть нам дана функция
, 
,
которую мы изобразим, как указано выше, через степенную функцию, первая производная ее будет равна:
так как 
,то первая производная может быть выражена через
.
Слагаемое, имеющее множитель +j
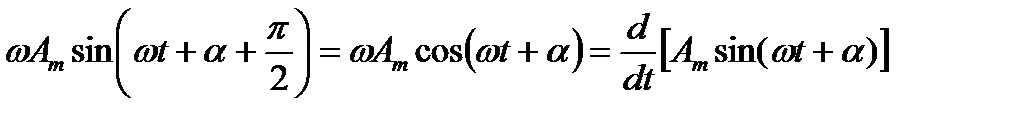как раз и представляет первую производную от заданной функции:
.
Поэтому мы дифференцирование по времени можем заменить простым умножением на оператор 
,
.
Точно так же
.
С другой стороны, если мы обозначим
через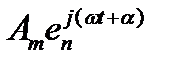 
,
то тот же интеграл выразится через
,
но так как
.
и мнимая часть равна
,
то мы видим, что для нахождения интеграла синусоидальной переменной величины достаточно разделить функцию на условный оператор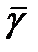 
.
Применим означенный способ к нахождению напряжения, которое должно быть приложено к цепи переменного тока, состоящей из сопротивления r, индуктивности L и емкости С при прохождении через эту цепь тока i=Imsinωt.
Как известно, искомое напряжение будет состоять из суммы мгновенных значений падения напряжения на активном сопротивлении r, индуктивности L и ёмкости С. Последнее равно количеству притекшего к обкладкам электричества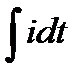 
,деленному на емкость С:
.
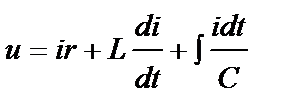Заменяя первую производную и интеграл через оператор 
, мы получаем, что искомое напряжение при прохождении тока 
будет равно:
.
Изобразим комплекс, стоящий в скобках, через модуль и соответствующий угол:
,
, 
,
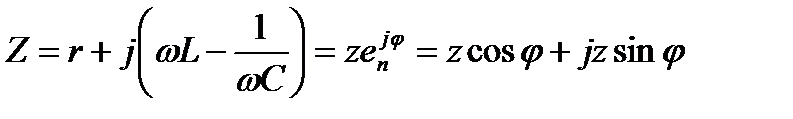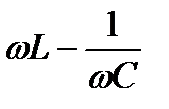откуда
и 
и подставим найденное выражение этого комплекса в уравнение напряжения:
.
Таким образом, получаем известное уже соотношение, что амплитуда искомого напряжения равна амплитуде тока, умноженной на полное сопротивление
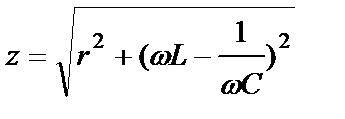
Рис. 3.32. Геометрическое представление комплексов для нахождения мощности переменного тока
|
.
Пользуясь последним уравнением, можно написать и выражение для мгновенного значения этого напряжения
.