При создании топографической карты земную поверхность изображают на плоскости. Изображение выпуклой поверхности на плоскости неизбежно связано с искажениями. Для уменьшения искажений земную поверхность проецируют на плоскость и изображают по частям. При этом используется проекция Гаусса-Крюгера, в которой поверхность земного эллипсоида делят меридианами на 60 шестиградусных зон. Каждую зону изображают на плоскости отдельно. В каждой зоне установлена своя система плоских прямоугольных координат.
Зоны нумеруют с запада на восток. Западным меридианом первой зоны является Гринвичский меридиан. Средний меридиан каждой зоны называется ее осевым меридианом.
На плоскости осевой меридиан зоны изображается прямой линией без искажения длин (рис. 7). Остальные меридианы зоны изображаются кривыми линиями, и поэтому они длиннее осевого меридиана, т. е. искажены. Экватор также изображается прямой линией. Осевой меридиан и экватор приняты за оси плоских прямоугольных координат зоны. Осевой меридиан служит осью абсцисс (х),линия экватора – осью ординат (у).
Абсциссы х отсчитывают от экватора к северу (положительные) и к югу (отрицательные). Для территории нашей страны абсциссы всегда положительны. Чтобы избежать отрицательных значений ординат y в западной половине зон, условились начало координат в каждой зоне сдвигать к западу на 500 км (рис. 7).
Чтобы различать одинаковые координаты, относящиеся к разным зонам, впереди к ординате у (на место тысяч километров) приписывают номер зоны.

Рис. 7. Система прямоугольных координат
Задача № 20. По географическим координатам точки: φ = 47°18' северной широты; λ= 70°30' восточной долготы, определить номер шестиградусной зоны, в которой расположена точка, и долготу осевого меридиана зоны.
Решение. Номер зоны n, в которой расположена точка, определяется ее географической долготой l:

Отбросив дробную часть, находим номер зоны. Следовательно, точка расположена в зоне № 12.
Если вычисляемый по формуле результат оказывается целым, – это значит, что точка расположена на границе зон п и(п – 1).
Долготу осевого меридиана зоны с номером п определяют по формуле:
λ° = 6°× п – 3° = 6° · 12 – 3° = 69°.
Задача № 21. По координатам точки хK = 5 671 890 м, уK = 8 656 300 м определить номер зоны, в какой половине зоны точка расположена, а также расстояние до нее от осевого меридиана зоны. Начертить схему.
Решение. Для определения номера зоны необходимо отделить, начиная с конца ординаты у,шестизначное число метров или трехзначное число километров. Оставшиеся одна или две цифры и являются номером зоны. В нашей задаче точка K располагается в зоне № 8.
Зная, что ордината осевого меридиана зоны равна у = 500 км, несложно определить, что точка K расположена в восточной половине зоны и удалена от осевого меридиана на расстояние 656,3 – 500 = 156,3 км (рис. 8). Абсцисса х показывает, что точка K удалена от экватора на 5671,89 км.

Рис. 8. Определения положения точки
по прямоугольным координатам
Для определения прямоугольных координат на карте нанесена так называемая километровая сетка в виде квадратов со сторонами, обычно равными одному километру в масштабе данной карты.
Нижняя линия километровой сетки имеет на рамке карты надпись 6065 (рис. 9). Это означает, что все точки этой линии имеют абсциссу х = = 6065 км.
Первая слева километровая линия, параллельная изображению осевого меридиана зоны, имеет надпись 4311. Здесь цифра 4 обозначает номер зоны, а ордината у = 311 означает, что все точки, расположенные на этой линии, находятся слева (западнее) от осевого меридиана зоны на расстоянии 500 – 311 = 189 км.
Полные значения координат подписаны только у крайних линий сетки. У всех промежуточных линий сетки подписаны сокращенные обозначения – только последние две цифры (десятки и единицы километров). Например, нижняя линия километровой сетки имеет обозначение 6065, а следующая над ней линия сетки обозначена только числом 66 км, а не 6066.
Задача № 22. Определить по карте прямоугольные координаты точки с отметкой 140,9 м, расположенной в квадрате 65×13. Указания квадрата даются по сокращенным координатам (рис. 9).
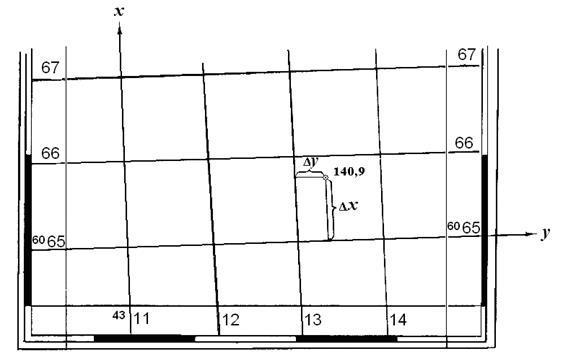
Рис. 9. Определение прямоугольных координат
Решение. Сначала записывают абсциссу нижней (южной) километровой линии квадрата, в котором находится точка, т. е. 6065 км, затем измеряют расстояние Δ х и, пользуясь линейным масштабом карты, определяют, чему оно равно на местности. Полученную величину Δ х = 870 м складывают с величиной абсциссы нижней линии:
х = 6 065 000 м + 870 м = 6 065 870 м.
Аналогичным путем определяют ординату точки. Записав значение ординаты левой (западной) стороны квадрата 4313 км, к нему прибавляют значение Δ у = 475 м.
у = 4 313 000 м + 475 м = 4 313 475 м.
Задача № 23. Даны географические координаты точки: φ = 58°34' северной широты, λ = 109° 12' восточной долготы.
Определить номер зоны, в которой точка расположена, и долготу осевого меридиана шестиградусной зоны.
Задача № 24. Даны прямоугольные координаты точки:
х = 5 261 358,10 м,
у = 14 386 592,14 м.
Определить номер зоны и в какой половине зоны точка расположена.
Задача № 25. Определить на карте У-34-37-В-в-4 прямоугольные координаты вершины горы Андогская с отметкой 160,6 м (квадрат 66×11).
Задача № 26. Определить по карте У-34-37-В-в-4, какие объекты имеют следующие прямоугольные координаты:
х 1 = 6 067 600 м, у 1 = 4 313 040 м;
х 2 = 6 066 610 м, у 2 = 4 311 000 м.
Задача № 27. Определите по карте У-34-37-В-в-4 прямоугольные координаты точек (см. табл. 2).
Таблица 2
| № п/п | Отметка и характеристика точки | Точка находится в квадрате | № п/п | Отметка и характеристика точки | Точка находится в квадрате |
| 186,6 край леса Северный | 68×13 | 139,4 урез воды оз. Черное | 65×13 | ||
| 142,0 р. Голубая | 65×12 | 140,5 ключ | 66×12 | ||
| 144,0 пересечение дорог | 65×14 | 149,7 пересечение дорог | 66×12 | ||
| 150,2 г. Лесная | 67×11 | 173,4 развилка тропинок | 68×13 | ||
| 141,2 пересечение дорог | 66×13 | 212,8 г. Михалинская | 68×12 | ||
| 126,6 урез воды р. Андога | 66×11 | 137,5 родник | 67×11 | ||
| 147,0 родник | 66×12 | 171,3 г. Карьерная | 67×13 | ||
| 180,0 развилка тропинок | 67×11 | 156,9 г. Голая | 65×11 |