Алгебра и теория чисел Толстиков А.В.
Раздел 1. 1. Введение в алгебру и геометрию
Курс 1. Семестр 1. Лекция 1.1. Множества
План
1. Основные понятия логики. 2. Множества. Подмножества. 3. Операции над множествами.
4. Декартово произведение множеств.
Литература: Ермаков В.И. с. 276-280. Ильин В.А., с.183-195. Шнейдер В.Е. 285-296. Кремер Н.Ш. 251-266.
Основные понятия логики.
Основные понятия логики высказывание и предикат. Под высказыванием понимается повествовательное предложение, о котором можно сказать только одно из двух истинно это предложение или ложно. Определения, вопросительные восклицательные предложения высказываниями не являются. Если высказывание истинно, то его значение будем считать равным 1 ("истина"), если ложно - равным 0 ("ложно"). Условимся обозначать высказывания прописными латинскими буквами: A, B, C, …Высказывания обозначаем большими буквами.
Введем логические операции над высказываниями, которые позволяют из одних высказываний строить другие более сложные.
Определение 1.1. Дизъюнкцией двух высказываний А и В называется высказывание, обозначаемое А Ú В, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний А или В.
Дизъюнкция называется логическим сложением. В русском языке знаку "Ú" соответствует союз "или", понимаемый в смысле "хотя бы одно из …". Символ A Ú B читается " А или В ", " А дизъюнкция В ".
Например, "5 < 7 или 5 = 2" - истинное высказывание, "2+2 = 7 или 5 = 2" - ложное высказывание.
Определение 1.2. Конъюнкцией двух высказываний А и В называется высказывание, обозначаемое А & В или А Ù В, которое истинно тогда и только тогда, когда истинны одновременно оба высказывания А и В.
Конъюнкция называется логическим умножением. В русском языке знаку "&" соответствует союз "и". Символ A & B читается " А и В ", " А конъюнкция В ".
Например, "5 < 7 и 2+2 = 4" - истинное высказывание, "2 > 7 и 5+2 = 7" - ложное высказывание.
Определение 1.3. Импликацией двух высказываний А и В называется высказывание, обозначаемое А Þ В, которое ложно тогда и только тогда, когда высказывание А истинны, а В ложно.
При этом говорят, что А - посылка, В - заключение.
Импликация называется логическим следованием. Символ A Þ B читается "если А, то В ", "из А следует В ", " А влечет В ", " А импликация В ".
Например, "если 5 < 7, то 2+2 = 4" - истинное высказывание, "если 2 > 7, и 5+2 = 7" - ложное высказывание.
Определение 1.4. Эквиваленцией двух высказываний А и В называется высказывание, обозначаемое А Û В, которое истинно тогда и только тогда, когда высказывание А и В истинны или ложно одновременно.
Символ A Û B читается " А тогда и только тогда, когда В ", " А эквивалентно В ", " А необходимо и достаточно для В ".
Например, "5 < 7 тогда и только тогда, когда 2+2 = 4" - истинное высказывание, "2 > 7 эквивалентно 5+2 = 7" - ложное высказывание.
Определение 1.4. Отрицанием высказывания А называется высказывание, обозначаемое 
или Ø А, которое ложно тогда и только тогда, когда высказывание А истинны.
Операции отрицания соответствует в русском языке частица "не". Символ читается "не А ", "неверно, что А ".
Определения 1.1-1.5 можно записать в виде так называемых таблиц истинности (для компактности все таблицы сведены в одну):
| A | B | A Ú B | A & B | A Þ B | A Û B |
|
Некоторые логические операции можно выразить через другие, используя равносильности следующей теоремы.
Теорема 1.3. Для любых переменных высказываний А, В, С справедливы свойства:
1. A Þ B º Ø A Ú B; 2. A Û B º (A Þ B)&(B Þ A); 3. A Û B º (Ø A Ú B)&(Ø B Ú A);
4. Ø(A Ú B) º Ø A & Ø B; 5. Ø(A & B) º Ø A Ú Ø B (законы А. де Моргана);
6. Ø(A Þ B) º A & Ø B; 7. Ø(A Û B) = (A & Ø B) Ú (B & Ø A).
Замечание. Доказываются эти равенства с помощью таблиц истинности. Равенства 4-7 используются для построения отрицаний.
Множества. Подмножества.
В математике понятие множества является одним из основных. Для него имеется много общеизвестных синонимов (класс, совокупность, группа, семейство и т.п.). Создатель теории множеств немецкий математик Г. Кантор (1845-1918) говорил, что множество - есть совокупность объектов, рассматриваемых как единое целое. Объекты, из которых состоит данное множество, называются элементами.
Условимся обозначать множества прописными латинским буквами А, В, …, а их элементы - строчными буквами а, в, … Символы аÎ А и аÏА обозначают соответственно, что "элемент а принадлежит множеству А ", "элемент а не принадлежит множеству А ". N, Z, Q и R соответственно обозначают множества всех натуральных, целых, рациональных и действительных чисел.
Если множество конечное, то его можно записать с помощью перечисления всех его элементов в списке, который заключается в фигурные скобки. Число элементов в конечном множестве A обозначается символом | A |.
Если множество содержит элементы и не является конечным, то оно называется бесконечным. Такие множества обычно задаются указанием характеристического свойства, которым обладают его элементы: A = { x |P(x)}, P(x) – свойство, которым обладают элементы множества. Например, множество четных чисел можно записать в виде { x | x - целое число и x делится на 2} или { x | x Î Z и x M2}, или { x Î Z | x M2}. Некоторые бесконечные множества можно записать в виде бесконечной последовательности. Например, множества N всех натуральных чисел и множество Z всех целых чисел:
N = {1, 2, 3, …}, Z = {…, -3, -2, -1, 0, 1, 2, 3, … }.
Множество Q всех рациональных чисел можно задать так:
Q = { x | x = m/n, m Î Z, n Î Z, n ¹ 0}.
Определение 2.1. Говорят, что множество А включено во множество В и пишут А Í В, если каждый элемент множества А принадлежит множеству В.
Если А Í В, то так же говорят: А содержится в B, В содержит А, А есть часть В, А есть подмножество В, В есть надмножество А.
Множество называется пустым и обозначается символом Æ, если оно не содержит ни одного элемента.
Теорема 2.1. Для любых множеств А, В, С справедливы свойства:
1. Æ Í В, 2. А Í А (рефлексивность), 3. если А Í В и В Í С, то А Í С (транзитивность).
Доказательство. ТУ 2.1.
Замечание. Теоретические упражнения должны быть проработаны студентами самостоятельно или на практических занятиях.
В приложениях теории множеств обычно рассматриваются только такие множества, которые содержаться в некотором фиксированном множестве U, называемом универсальным множеством. Понятие универсального множества - понятие относительное. Например, универсальное множество в планиметрии - множество всех точек плоскости, а в стереометрии - множество всех точек пространства.
Диаграммами Эйлера-Венна называются плоские фигуры (например, круги), с помощью которых наглядно изображаются множества, графически иллюстрирующие отношения между множествами и свойства булевых операций. Л. Эйлер - швейцарский математик, жил в России (1707-1783); Дж. Венн - английский логик и математик (1834-1923).
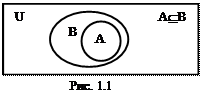Определение 2.2. Говорят, что множество A равно множеству B и пишут A= B, если выполняются два условия:
(1) каждый элемент множества A принадлежит множеству B
(2) каждый элемент множества B принадлежит множеству А.
Символ A ¹ B обозначает, что множество A не равно множеству B.
Теорема 2.2. Для любых множеств A, В, C справедливы свойства:
1. А = A (рефлексивность), 2. если A = B, то B = A (симметричность), 3. если A = B и B = C, то A = C (транзитивность).
Доказательство. ТУ 2.2.
Теорема 2.3. Множества A и B равны тогда и только тогда, когда A Í B и B Í С.
Доказательство. ТУ 2.3.
Определение 2.3. Говорят, что множество A строго включено во множество B и пишут A Ì B, если A Í B и A ¹ В.
Если A Ì B, то говоря, что A - собственное подмножество множества B. Например, {4, 5} Ì {3, 4, 5} Ì N Ì Z Ì Q Ì R. Если A не является строго включенным в B, то пишут A Ë B. Например, {1, 4, 5} Ë {3, 4, 5}.
Теорема 2.4. Для любых множеств A, В, C справедливы свойства:
1. А Ë А (антирефлексивность), 2. если А Ì В, то B Ë A (ассимметричность), 3. если А Ì В и В Ì С, то А Ì С (транзитивность).
Доказательство. ТУ 2.4.
Определение 2.4. Множество всех подмножеств множества А называется булеаном множества А и обозначается символом P (А) или 2 А
Пример. Булеан множества A = {1, 2}, P (А) = {Æ, {2}, {1}, {1, 2}.
Теорема 2.5. Булеан конечного множества содержит 2| A | различных подмножеств.
Доказательство. Пусть | A | = n. Доказываем индукцией по n. Пусть n =0. Тогда А = Æ, P (А) = {Æ} и | P (А)| = 1. Предположим, что утверждение верно для любого множества В, содержащего n -1 элементов и докажем его для n –элементного множества А= { a 1, a 2,…, an }. Тогда любое подмножество либо не содержит элемент an либо содержит an. Если оно не содержит элемент an, то оно является подмножеством В множества { a 1, a 2,…, an -1}. Таких подмножеств 2 n- 1. Если оно содержит элемент an, то оно имеет вид В È{ an }, где В подмножества { a 1, a 2,…, an -1}. Таких подмножеств 2 n- 1. Тогда всего подмножеств в множестве 2 n- 1 +2 n- 1=2 n.
Упражнения: 2.1. Доказать свойства теоремы 2.1.
2.2. Доказать свойства теоремы 2.2.
2.3. Доказать свойства теоремы 2.3.
2.4. Доказать свойства теоремы 2.4.
2.5. Установить, что множества A = { x Î R | x 2-2 x +2<0} и B = ={ x Î R | log x -1 (1- x)>0} - пустые.