Рассмотрим функцию: y=kx, k≠0.
Коэффициент k – может принимать любые действительные значения, кроме нуля. Для простоты начнем разбор функции со случая, когда k=1.
Построим график функции: y=1x.
Как всегда начнем с построения таблицы. Правда в этот раз придется разделить нашу таблицу на две части. Рассмотрим случай, когда x>0.
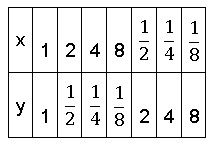 Нам нужно отметить шесть точек с координатами (x;y), которые приведены в таблице и соединить их линией.
Нам нужно отметить шесть точек с координатами (x;y), которые приведены в таблице и соединить их линией. 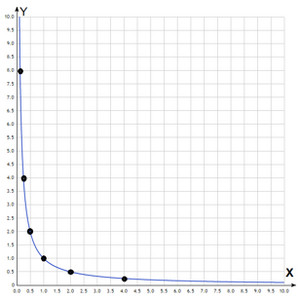
Теперь посмотрим, что у нас получается при отрицательных х. 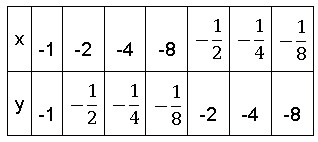 Поступим тем же образом, отметим точки и соединим их линией.
Поступим тем же образом, отметим точки и соединим их линией. 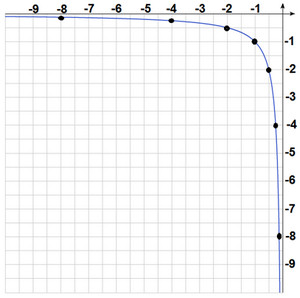 Два кусочка графика мы построили, давайте объединим их.
Два кусочка графика мы построили, давайте объединим их.
График функции y=1x.
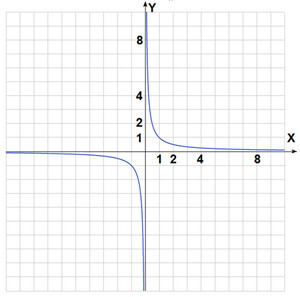 График такой функции называется "Гиперболой".
График такой функции называется "Гиперболой".
Согласитесь, график выглядит довольно-таки красиво, и он симметричен относительно начала координат. Если провести любую прямую, проходящую через начало координат, из первой в третью четверть, то она пересечет наш график в двух точках, которые будут одинаково отдалены от начала координат.
Гипербола состоит из двух, симметричных относительно начала координат, частей. Эти части называются, ветвями гиперболы.
Ветви гиперболы в одном направлении (влево и вправо) все больше и больше стремятся к оси абсцисс, но никогда не пересекут ее. В другом направлении (вверх и вниз) стремятся к оси ординат, но также никогда не пересекут ее (так как на ноль делить нельзя). В таких случаях, соответствующие линии называются асимптотами. График гиперболы имеет две асимптоты: ось х и ось у.
У гиперболы есть не только центр симметрии, но и ось симметрии. Ребята, проведите прямую y=x и посмотрите, как разделился наш график. Можно заметить, что если часть, которая расположена выше прямой y=x, наложить на часть, которая располагается ниже, то они совпадут, это и означает симметричность относительно прямой.
Мы построили график функции y=1x, но что будет в общем случае y=kx, k>0.
Графики практически не будут отличаться. Будет получаться гипербола с теми же ветвями, только чем больше k, тем дальше будут удалены ветви от начала координат, а чем меньше k, тем ближе подходить к началу координат.
Например, график функции y=10x выглядит следующим образом. 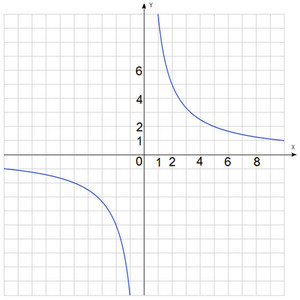 График стал "шире", отдалился от начала координат.
График стал "шире", отдалился от начала координат.
А как быть в случае отрицательных k? График функции y=−f(x) симметричен графикуy=f(x) относительно оси абсцисс, нужно перевернуть его "вверх ногами".
Давайте воспользуемся этим свойством и построим график функции y=−1x.
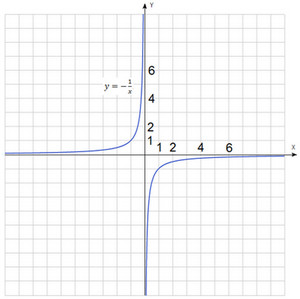
Обобщим полученные знания.
Графиком функции y=kx, k≠0 является гипербола, расположенная в первой и третье (второй и четвертой) координатных четвертях, при k>0 (k<0). Он симметричен относительно начала координат и оси координат – асимптоты гиперболы.
Свойства функции y=kx, k>0
1. Область определения: все числа, кроме х=0.
2. y>0 при x>0, и y<0 при x<0.
3. Функция убывает на промежутках (−∞;0) и (0;+∞).
4. Функция не ограничена ни сверху, ни снизу.
5. Наибольшего и наименьшего значений нет.
6. Функция непрерывна на промежутках (−∞;0)U(0;+∞) и имеет разрыв в точке х=0.
7. Область значений: (−∞;0)U(0;+∞).
Свойства функции y=kx, k<0
1. Область определения: все числа кроме х=0.
2. y>0 при x<0, и y<0 при x>0.
3. Функция возрастает на промежутках (−∞;0) и (0;+∞).
4. Функция не ограничена ни сверху, ни снизу.
5. Наибольшего и наименьшего значений нет.
6. Функция непрерывна на промежутках (−∞;0)U(0;+∞) и имеет разрыв в точке х=0.
7. Область значений: (−∞;0)U(0;+∞).
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
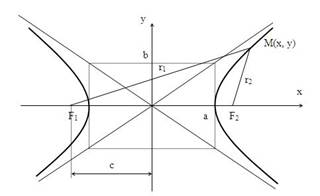
Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описыватьсяуравнением:

Числа 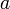 и
и 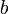 называются соответственно вещественной и мнимой полуосями гиперболы.
называются соответственно вещественной и мнимой полуосями гиперболы.
Связанные определения
· Осью гиперболы называется прямая, соединяющая её фокусы.
· Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы  .
.
· Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественнойполуосью гиперболы 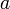 .
.
· Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы 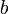 .
.
По определению | r 1 – r 2 | = 2 a. F 1, F 2 – фокусы гиперболы. F 1 F 2 = 2 c.
Выберем на гиперболе произвольную точку М(х, у). Тогда:
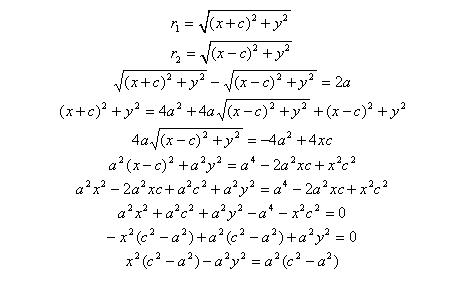
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
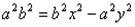
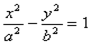
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью.
Ось 2 b называется мнимой осью.
Гипербола имеет две асимптоты, уравнения которых 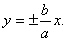
Определение. Отношение 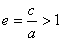 называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а 2 = b2
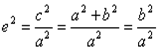 :
:
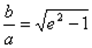
Если а = b, e = 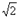 , то гипербола называется равнобочной (равносторонней).
, то гипербола называется равнобочной (равносторонней).
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: 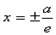
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.
Доказательство. Изобразим схематично гиперболу.
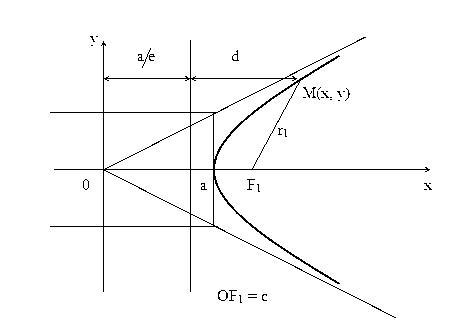
Из очевидных геометрических соотношений можно записать:
a / e + d = x, следовательно d = x – a / e.
(x – c) 2 + y2 = r 2
Из канонического уравнения: 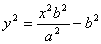 , с учетом b2 = c2 – a2:
, с учетом b2 = c2 – a2:
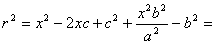
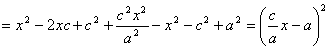
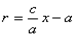
Тогда т.к. с/ a = e, то r = ex – a.
Итого: 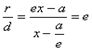
Для левой ветви доказательство аналогично. Теорема доказана
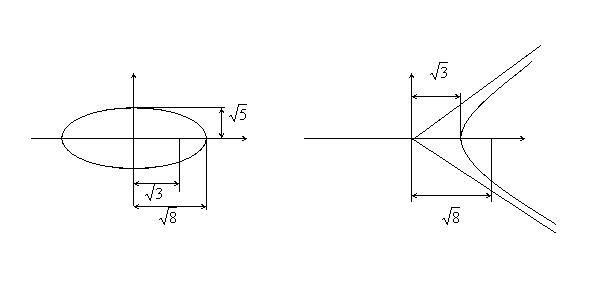
Пример 1. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса 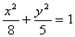
Для эллипса: c 2 = a2 – b2.
Для гиперболы: c2 = a2 + b2.
Уравнение гиперболы: 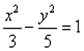
Пример 2. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением 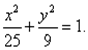
Находим фокусное расстояние c 2 = 25 – 9 = 16.
Для гиперболы: c2 = a2 + b2 = 16, e = c / a = 2; c = 2 a; c 2 = 4 a2; a2 = 4;
b2 = 16 – 4 = 12.
Итого: 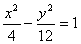 - искомое уравнение.
- искомое уравнение.