Поверхностные интегралы первого рода

Рассмотрим некоторую поверхность 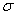. Из чего она состоит? Из точек с координатами «икс, игрек, зет». Отлично.

Пусть функция трёх переменных определена в каждой точке данной поверхности. Что это значит? Это значит, что каждой точке поверхности ставится в соответствие определённое число – образно говоря, «муравей» той или иной степени «упитанности», который «сидит» на бесконечно малом участке 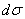данной поверхности.

Наверное, многие предчувствуют дальнейшее развитие темы. Согласно общему принципу интегрирования, интеграл объединяет этих «муравьёв» по всем бесконечно малым площадям 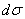поверхности .

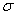И нетрудно понять, что при 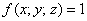он в точности равен площади самой поверхности:

Как решать поверхностные интегралы 1-го рода?

Пример 1

С помощью поверхностного интеграла найти площадь фрагмента плоскости , расположенного в 1 октанте.

…извращение, конечно, но что поделать =)

Решение: сначала выполним чертёж. В большинстве случаев без него никак. Для этого запишем уравнение плоскости в отрезках:

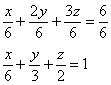
По причине нахлынувшей ностальгии все чертежи этого урока я выполню от руки. Да и не только по этой – думается, ручное построение поверхностей будет актуально ещё достаточно долго:

По условию, площадь треугольника 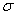нужно найти с помощью поверхностного интеграла 1-го рода:

Если поверхность задана функцией двух переменных 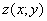, то поверхностный интеграл можно свести к двойному интегралу по формуле:

, где – проекция поверхности 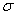на плоскость . Занесите в свой справочник.

В нашем случае речь идёт о площади и поэтому формула упрощается:
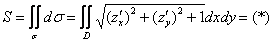(прерываемся для промежуточных действий)

Перепишем уравнение плоскости в функциональном виде:

и найдём частные производные первого порядка, они здесь элементарные:

продолжаем:

С областью (на чертеже заштрихована) трудностей нет – остановлюсь лишь на том, как найти уравнение прямой, которая лежит в плоскости . Для этого в уравнении плоскости обнуляем «лишнюю» зетовую переменную:

откуда удобно выразить:

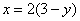
Двумерный чертёж настоятельно рекомендую даже читателям с высоким уровнем подготовки, ибо «проглючить» тут может как дважды два:

Ну и очевидно, что порядок обхода области будет таким:

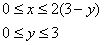
После чего решение выходит на финишную прямую:

Ответ:

Желающие могут найти пару подходящих векторов и проверить результат с помощью векторного произведения.

Но это ещё далеко не всё. Зададимся следующим вопросом: а почему поверхность нужно проецировать именно на плоскость ? Чем другие координатные плоскости и другие переменные хуже? Да ничем! Давайте окончательно отбросим все комплексы и освоим универсальную технику интегрирования:

Формула вторая: если поверхность 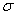выражена функцией , то:

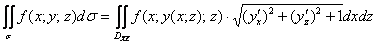, где 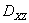– проекция данной поверхности на плоскость .

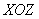В нашем случае:

Перепишем уравнение плоскости в виде:

и возьмём частные производные:

Теперь в уравнении плоскости обнулим «лишнюю» игрековую координату, выяснив тем самым уравнение прямой, которая лежит в плоскости :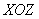

Выполним чертёж проекции :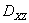

(на пространственном чертеже это левый «стоячий» треугольник)

Порядок обхода области:

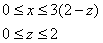
таким образом:

Что мы и ожидали увидеть.

Самостоятельно запишите формулу вычисления поверхностного интеграла для случая, когда поверхность выражена функцией и решите задачу третьим способом – проецированием поверхности на плоскость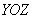

Зачем нужна эта экзотика?

Нужна. И более того, не такая уж это и экзотика. В некоторых задачах проецирование на «родную» плоскость сопряжено с трудностями или вообще недопустимо (когда поверхность параллельна оси 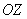). Или получается трудный интеграл. И поэтому всегда нужно держать на заметке, что существуют альтернативные пути!

Следующее задание для самостоятельного решения:

Пример 2

С помощью поверхностного интеграла вычислить площадь поверхности 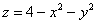, расположенную в верхнем полупространстве.

Тот редкий случай, когда можно обойтись без чертежа – слишком уж каноничен параболоид. Следует отметить, что в этом примере выгодно именно «классическое» интегрирование с проецированием поверхности на плоскость . Кстати, результат будет любопытно сравнить с ответом Примера 2 статьи Площадь поверхности вращения.

Добавим в наш интеграл какую-нибудь интересную функцию…. Посвящается «математической» доменной зоне и Гуглу в частности:)

Пример 3

Вычислить интеграл , где 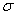– фрагмент конической поверхности 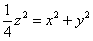, заключенный между плоскостями .

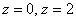Решение: порядок построения чертежа подробно рассмотрен в статье о поверхностях, но, тем не менее, кратко повторю: на высоте данная плоскость пересекает конус по:
– окружности единичного радиуса:

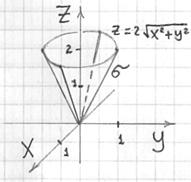
-«колпак» проще спроецировать на «стандартную» плоскость:

и воспользоваться формулой

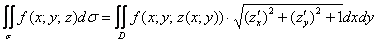
Верхнюю часть конуса задаёт функция:

Найдём её частные производные:

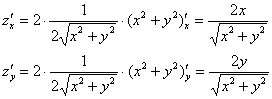
И здесь сразу удобно упростить корень:

Таким образом, по формуле (см. выше):

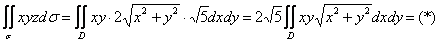
Тут, конечно, лучше перейти к полярным координатам:

И из «плоского» чертежа очевиден порядок обхода:

Постараемся ничего не упустить:

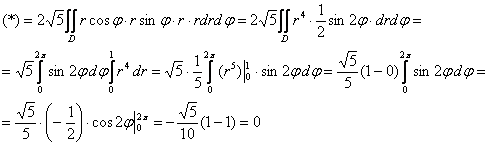
Ответ:

Может ли поверхностный интеграл равняться нулю? Конечно. И отрицательному числу тоже. Ведь подынтегральная функция может принимать любые значения.

Рассмотрим два альтернативных пути. Вкратце разберу порядок действий:

Способ второй. Проецируем конус на плоскость 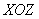(получится треугольник) и используем формулу ,

причём, интеграл придётся представить в виде суммы двух интегралов:
,
где 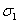– это левая часть конуса, которую нужно выразить функцией:

а – его правая часть:

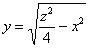
И противоположные «игрековые» знаки приводят к забавной коллизии – в результате интегралы взаимоуничтожаются и сразу получается ноль (если не понятно, почему так, начните решать). А казалось, это был совершенно нерациональный путь! Но то, конечно, частный счастливый случай.

Здесь, кстати, мы столкнулись со свойством аддитивности, которое наряду со свойством линейности, разумеется, справедливо и для поверхностных интегралов. Иными словами, поверхность можно разделить на несколько кусков, вычислить интеграл по каждому из них, после чего просуммировать результаты.

Способ третий. Проецируем конус на плоскость 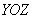(тоже получится треугольник) и используем формулу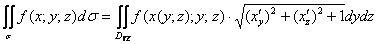

Аналогично – интеграл представляем как сумму интегралов по ближней 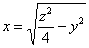и по дальней от нас части конуса; результаты так же взаимоуничтожаются и получается ноль.

Рассмотренная поверхность тоже «хорошо» проецируется на все координатные плоскости, однако так бывает далеко не всегда. Не такая уж редкость, когда в нашем распоряжении оказываются два, а то и единственный путь решения. Соответствующие примеры будут на уроке Поток векторного поля. Но пока с ними повременим.

Следующее задание для самостоятельного решения:

Пример 4

Вычислить интеграл 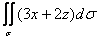, где 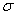– часть плоскости 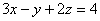, ограниченная координатными плоскостями. Выполнить чертёж.

Моя версия решения в конце урока.

В рамках данной статьи я не буду рассматривать общую формулу вычисления поверхностного интеграла 1-го рода для параметрически заданной поверхности. По той причине, что в большинстве учебных курсов всё дело ограничивается частными декартовыми формулами. Однако читателям-«технарям» просто необходимо ознакомиться с этим материалом – соответствующую информацию можно найти здесь (попроще) и здесь (посложнее). Там же, к слову, есть развёрнутая теория и дополнительные примеры.

И в заключение параграфа коротко о «главном » физическом смысле рассмотренного интеграла:

если поверхность 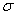представляет собой тонкую оболочку (железную, пластмассовую и т.д.; не обязательно однородную), а функция характеризует её плотность в каждой точке , то поверхностный интеграл 1-го рода численно равен массе данной оболочки: .

Логично. У криволинейного интеграла 1-го рода, напоминаю, была масса кривой.