Задание: Выполнить уравнивание обратной многократной засечки (рис.1) параметрическим способом по направлениям.
Вычислить:
Уравненные координаты 
и 
определяемого пункта и уравненный дирекционный угол нулевого диаметра лимба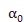 
.
Оценить точност ь:
a. Уравненных координат определяемого пункта Р.
b. Дирекционного угла и длины стороны Р-3.
Рис.1 – Схема угловой засечки
Исходные данные: Даны координаты пяти исходных пунктов (табл.1) и пяти измеренных направлений (табл.2); вычисленные приближенные координаты определяемого пункта Р.
Таблица №1. Координаты исходных пунктов
| № пункта | Х | У |
| 7038.259 | 10021.897 | |
| 8931.452 | 11982.156 | |
| 8089.743 | 14591.085 | |
| 5647.209 | 14038.842 | |
| 4201.839 | 13471.423 |
Координаты исходных пунктов являются одинаковыми для всех студентов группы.
Таблица №2. Измеренные направления***
| № направления | Измеренное направление |
| 00˚00'00,0" | |
| 58˚44'07,1" | |
| 114˚14'29,6" | |
| 171˚46'43,9" | |
| 218˚28'26,1" |
Приближенные координаты определяемого пункта**:
м
м
Приближенные координаты определяемого пункта и значения направлений необходимо смоделировать в программе MATRIX.exe.
** Приближенные координаты моделировать с точностью 
.
*** Направления моделировать с точностью mN = 3".
В условиях дистанционного обучения: Для моделирования варианта используем таблицы приложения XI «Таблицы нормальных величин t» из Практикума по ТМОГИ стр339, авторы Большаков В.Д., Маркузе Ю.И. (есть в свободном доступе в интернете). Каждый студент из таблиц выписывает семь значений начиная со своего номера в журнале Например, для варианта 6 выписываем -0,5863; 1,1572;-0,4428; -0,3944; 0,8319; 0,9780; 0,4083.Первые 5 значений используем для моделирования направлений, 6 и 7 для моделирования приближенных координат пункта Р.
Направления моделируем с точностью 3”, то есть каждое значение надо умножить на 3, получаем: -1,8; +3,4; -1,3 и т. д. Затем эти значения прибавляем (с учетом знака) к секундам направлений. Получаем 1) 359˚59'58,3", 2) 58˚44'10,5", 3) 114˚14'28,3" и т.д.
При моделировании приближенных координат умножаем 6 и 7 значения на 0,02 и прибавляем к значениям +(-0,0194)=6048,203м; + 12437,851м.
Порядок работы
1.Выберем неизвестные и обозначим их:
Неизвестными в данной задаче (обозначим их символом x с индексом) являются дирекционный угол нулевого диаметра лимба α0 (его называют ориентирующим углом) и координаты определяемого пункта ХР и УР.
2.Составим уравнение связи между измеренными значениями и неизвестными.
Так как измеренное направление N i есть угол между стороной P-i (i - номер исходного пункта) и нулевым диаметром лимба α0 (см. рис.1), то его можно выразить через соответствующие дирекционные углы:
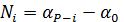(1)
Дирекционные углы получают из решения обратной геодезической задачи.
С учетом этого уравнения связи приобретут вид:
, (2)
где Уi и Хi координаты i– го исходного пункта, Хр и Ур– определяемого, У1 и Х1 координаты 1 – го исходного пункта
3.Составим параметрическое уравнение поправок:
Параметрическое уравнение поправок 
для направления с пункта P на пункт i в подробной записи будет иметь вид:
(3)
где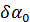 
- поправка к дирекционному углу нулевого диаметра лимба или к ориентирующему углу (любое название правильно), 
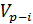- параметрическое уравнение поправок дирекционного угла направления P- i.
Параметрическое уравнение поправок дирекционного угла стороны P- i равно:
(4)
где ρ - коэффициент перехода от радианной к градусной мере (ρ=206265"), 
- длина стороны P-i, 
, 
, 
, 
- поправки в соответствующие приближенные координаты пунктов P и i.
Так как пункт i - исходный и безошибочный, поправки 
и 
равны нулю.
С учетом этого параметрическое уравнение поправок для направления с определяемого пункта P на исходный пункт i приобретет вид:
(5)
Как видим, уравнение поправок в данном случае содержит три неизвестных параметра: , ,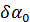 
.
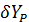В общем виде для і – го направления оно будет записано так:
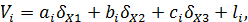
где ai – коэффициент при неизвестном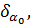 
bi - при 
, ci - при 
.
В данном случае они равны:
. (6)
4.Вычислим приближенные значения неизвестных коэффициенты и свободные члены уравнений поправок
Свободные члены параметрических уравнений поправок для направлений вычисляют по формуле:
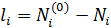(7)
где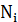 
- измеренные направления, 
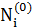- приближенные значения направлений, которые вычисляются по формуле:
(8)
Приближенные координаты 
определяемого пункта Р обычно вычисляют по хорошо известным геодезическим формулам с использованием измеренных направлений и координат исходных пунктов 
, на которые опирается обратная засечка.
В данном случае приближенные координаты определяемого пункта Р известны (смоделированы), координаты исходных пунктов приведены в исходных данных.
Вычисление коэффициентов и свободных членов уравнений поправок можно выполнить по формулам (6) и (7), а можно воспользоваться программой MATRIX.exe.
Вычисление коэффициентов уравнений поправок по формулам (6) удобно выполнять в таблице 3.
Таблица 3 Вычисление коэффициентов уравнений поправок
| Элемент сети | Номер пункта | ||||
| Уi | 10021.897 | 11982.156 | 14591.085 | 14038.842 | 13471.423 |
| Yр(0) | 12437.843 | ||||
| Уi - Yр(0) | -2415.946 | -455.687 | 2153.242 | 1600.999 | 1033.580 |
| Xi | 7038.259 | 8931.452 | 8089.743 | 5647.209 | 4201.839 |
| Xр(0) | 6048.222 | ||||
| Xi - Xр(0) | 990.037 | 2883.230 | 2041.521 | -401.013 | -1846.383 |
| αi(0) | 292˚17'00,4" | 351˚01'07,8" | 46˚31'32,2 | 104˚03'43.0" | 150˚45'37,8" |
| Sin αi(0) | -0,925319 | -0,156110 | 0,725682 | 0,970034 | 0,488461 |
| Cos αi(0) | 0,379189 | 0,987740 | 0,688030 | -0,242971 | -0,872586 |
 = 
| 2610,932 | 2919,018 | 2967,197 | 1650,457 | 2115,991 |
= 
| 2610,932 | 2919,018 | 2967,197 | 1650,457 | 2115,991 |
| -73.10 | -11.03 | 50.44 | 121.23 | 47.62 |
| -29.95 | -69.79 | -47.83 | 30.26 | 85.06 |
При вычислениях в EXCEL следует помнить, что все действия с углами выполняют в радианной мере. Для перевода дирекционных углов в градусную меру надо воспользоваться опцией из мастера функций 
(слева от командной строки) ГРАДУСЫ из категории МАТЕМАТИЧЕСКИЕ. Знаки перед синусами и косинусами дирекционных углов в зависимости от четверти, в которой расположен угол, надо расставить самостоятельно и учесть их при вычислениях.
Вычисления с использованием программы MATRIX.exe выполняются в 7 пункте этой программы.
Рис.2 – Основное меню программы MATRIX.exe
На вопросы программы отвечаем, что не будем составлять условных уравнений, а будем составлять уравнения поправок. На вопрос о количестве пунктов указываем все пункты: и определяемый, и исходные, то есть шесть. Ввод координат пунктов начинаем с приближенных координат определяемого пункта, то есть, он всегда идет под первым номером. Соответственно первый твердый (исходный) пункт вводят под вторым номером, второй твердый под третьим и так далее (рис.3).
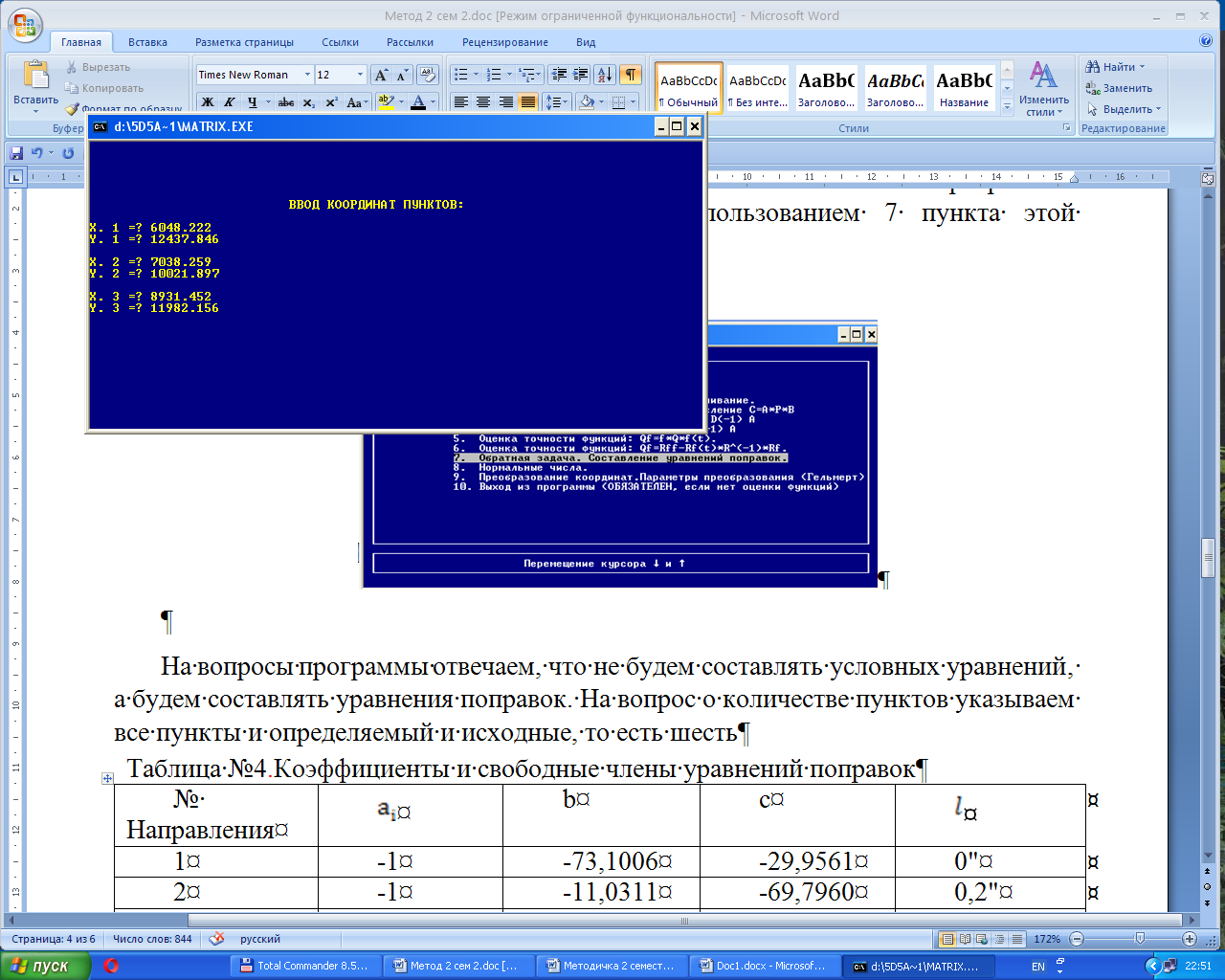
Рис.3 – Экран ввода координат в MATRIX.exe
После ввода координат всех пунктов, для вычисления коэффициентов уравнений поправок необходимо ввести номер соответствующего исходного пункта (рис.4 ), в программе он назван конечным (что соответствует обратной засечке).
Под номером один всегда подразумевается определяемый пункт, он назван начальным.
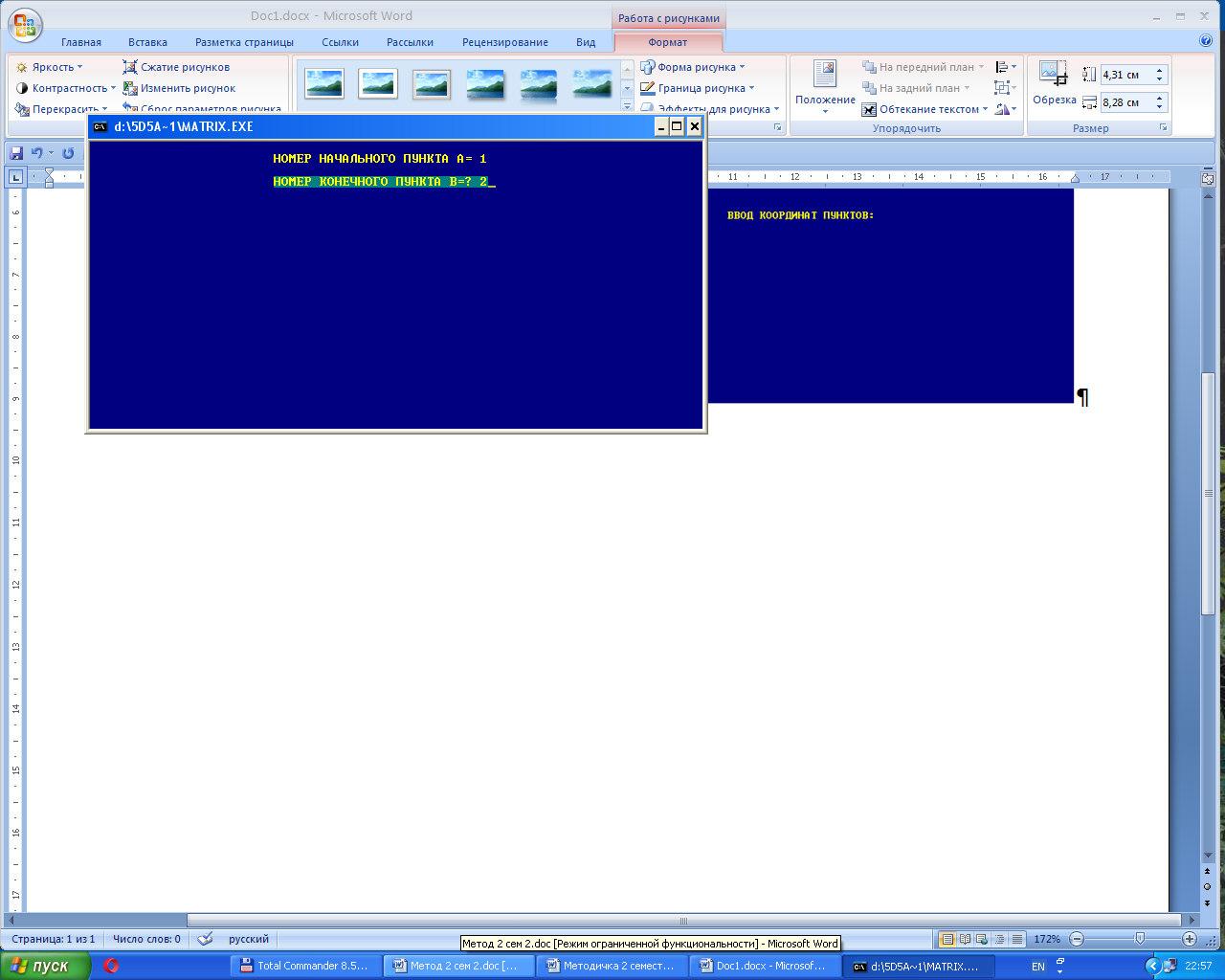
Рис.4 – Ввод номеров пунктов в MATRIX.exe
После ввода номера конечного пункта на экран выводится следующая (рис.5), из нужной нам, информация (приведен пример для направления 1-6):
- приближенный дирекционный угол направления (под названиемALFA) и приближенное направление. Градусы, минуты и секунды выводятся подряд, запятой отделяется только десятичные знаки секунд.
- коэффициенты уравнения поправок для направления. Так как для каждого направления нам нужны коэффициенты только для поправок в определяемый пункт, выписываем первые два коэффициента.
Рис.5 – Вывод информации в MATRIX.exe
После вычислений по последнему исходному (твердому) пункту завершаем работу программы.
В работе приводим результаты вычислений по программе в виде скриншотов экрана с необходимыми комментариями.
Коэффициенты уравнения поправок помещаем в матрицу А.
Ясно, что все коэффициенты при поправке в ориентирующий угол равны -1.
Приближенные значения направлений получают через вычисленные приближенные дирекционные углы по формуле (8). Их, а также свободные члены параметрических уравнений поправок для направлений, которые вычисляют по формуле (7), помещают в таблицу 4.
Таблица №4. Вычисление свободных членов уравнений поправок
| № направления | Приближенный дирекционный угол направления 
| Приближенное значение направления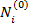 
| Измеренные значения направлений Ni | 
|
| 292˚17'00,4" | 00˚00'00,0" | 00˚00'00,0" | 0" | |
| 351˚01'07,8" | 58˚44'07,4" | 58˚44'07,1" | 0,3" | |
| 46˚31'32,2" | 114˚14'31,8" | 114˚14'29,6" | 2,2" | |
| 104˚03'43.0" | 171˚46'42,6" | 171˚46'43,9" | -1,3" | |
| 150˚45'37,8" | 218˚28'37,3" | 218˚28'26,1" | 11,2" |
6.Составим и решим нормальные уравнения, вычислим уравненные значения неизвестных параметров и их ско.
Как известно, в матричном виде нормальные уравнения записывают так:
Матрицу коэффициентов нормальных уравнений R вычисляют по формуле
(10)
где 
- транспонированная матрица 
, 
– матрица весов измерений.
Матрица свободных членов нормальных уравнений
b = АТРL, (11)
где L – матрица свободных членов уравнений поправок.
В матрицу свободных членов уравнений поправок 
выписываем 
из таблицы (4).
При уравнивании обратной засечки в уравнительных вычислениях используются координаты пунктов (метрическая мера) и измеренные направления (градусная мера). С целью установления соотношения между единицами измерения направлений и координат, вычисляют веса направлений. Так как измерения равноточные, вес у них будет одинаковый, но не равный нулю, он вычисляется следующим образом.
В качестве ошибки единицы веса принимаем среднюю квадратическую ошибку определяемого пункта:
, (12)
и вес направления получаем по формуле:
(13)
Средняя квадратическая ошибка направления 
, тогда вес каждого направления одинаков и равен:
Матрица весов измерений будет диагональной, так как измеренные направления независимы. Её размер –5х5:
Р =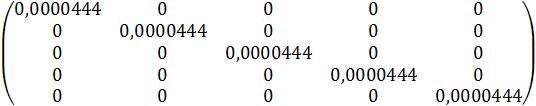 
Поправки к приближенным значениям неизвестных получим из решения нормальных уравнений:
(14)
Составление и решение нормальных уравнений можно выполнить как в программе EXCEL, так и в программе MATRIX.exe (рис.6).
Рассмотрим последовательность вычислений матрицы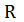 
в EXCEL.
Напомним, что при выполнении математических операций с матрицами необходимо перед началом вычислений определить размер результирующей матрицы, а затем на рабочем столе 
мышью выделить место, куда будет помещен результат вычислений. Для получения окончательного результата вычислений необходимо нажать одновременно три клавиши Ctrl, Shift и,OK (ENTER), это укажет программе, что она работает с массивами.
Все необходимые для вычислений операции: транспонирования, умножения и обращения матриц находятся в мастере функций (слева от командной строки знак 
. В появившемся окне, в разделе Категории из выпадающего меню выбираем категорию «Ссылки и массивы», «Массивы» или «Математические» (в разных версиях 
эта операция расположена в различных категориях), затем выбираем нужную операцию и нажимаем OK. Появляется окно, в котором необходимо указать матрицу (матрицы), с которой надо работать. Выделяем нужную матрицу мышью, Одновременно нажимают три клавиши Ctrl, Shiftи OK. Получаем результирующую матрицу.
В рассматриваем примере, получена матрица коэффициентов нормальных уравнений:
= 
Матрица свободных членов нормальных уравнений
Обратная матрица
= 
И вектор решения
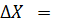
Для решения этой задачи по программе MATRIX.exe нам понадобится расширенная матрица коэффициентов уравнений поправок , дополненная столбцом свободных членов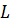 
(таблица 5) и веса измерений 
. Они уже получены ранее.
Таблица №5. Коэффициенты и свободные члены уравнений поправок
| № направления | 
| b | c | 
|
| -1 | -73,1006 | -29,9561 | 0" | |
| -1 | -11,0311 | -69,7961 | 0,3" | |
| -1 | 50,4458 | -47,8284 | 2,2" | |
| -1 | 121,2293 | 30,3651 | -1,3" | |
| -1 | 47,6148 | 85,0588 | 11,2" |
Для начала уравнивания запускаем программу MATRIX.exe и выбираем в меню пункт №2 «МНК (параметрический способ)»:
Рис. 6 – Меню программы MATRIX.exe
На заданный программой вопрос «хотите выполнить решение по МНК» (рис. 7) отвечаем «да», т.е. вводим латинскую букву «Y»
Рис. 7 – Запрос на решение программы MATRIX.exe
Программа напоминает (рис. 8), что в процессе вычислений можно оценить выбранную функцию, и после нажатия любой клавиши спрашивает, есть ли сохраненные данные на диске.
Рис. 8–Запрос о данных в программе MATRIX.exe
Так как данные в процессе работы не сохранялись, отвечаем "N".
Программа тут же предлагает выбрать имя файла (рис.9), где будут храниться результаты вычислений. Выбираем имя файла, например, "primer1" и вводим его.
Рис. 9 – Выбор имени файла в программе MATRIX.exe
После этого программа сразу предлагает начать ввод расширенной матрицы (рис.10), она запрашивает количество строк и столбцов в ней. Рассмотрим пример для матрицы 8х5.
Рис. 10 – Запрос о размерах матрицы в программе MATRIX.exe
Количество строк и столбцов в расширенной матрице 
, соответственно, 8 и 5, после ввода этих цифр, начинаем построчно (рис.11) вводить элементы расширенной матрицы. Помним, что последний столбец - это вектор
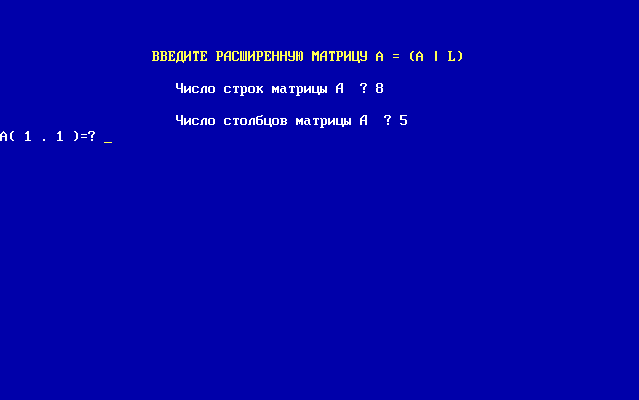
Рис. 11 – Ввод элементов расширенной матрицы
После ввода всех элементов расширенной матрицы программа задает вопрос о наличии ошибок при вводе, вводим "N", если ошибок нет. Следует обратить внимание, что в рассматриваемом примере расширенная матрица имеет размер 5х4.
Далее необходимо указать программе, равноточны или нет результат измерений. Если они равноточны, на вопрос: "Матрица Р единичная? " отвечаем "Y", после чего надо будет ввести вес равный 1. Так как уравниваются неравноточные измерения, на вопрос отвечаем "N". На вопрос «Матрица Р = р*Е», отвечаем "Y",в нашей сети веса всех измерений одинаковые. Вводим вес измерений.
В результате вычислений по программе получены (рис.12,13,14,15) следующие результаты:
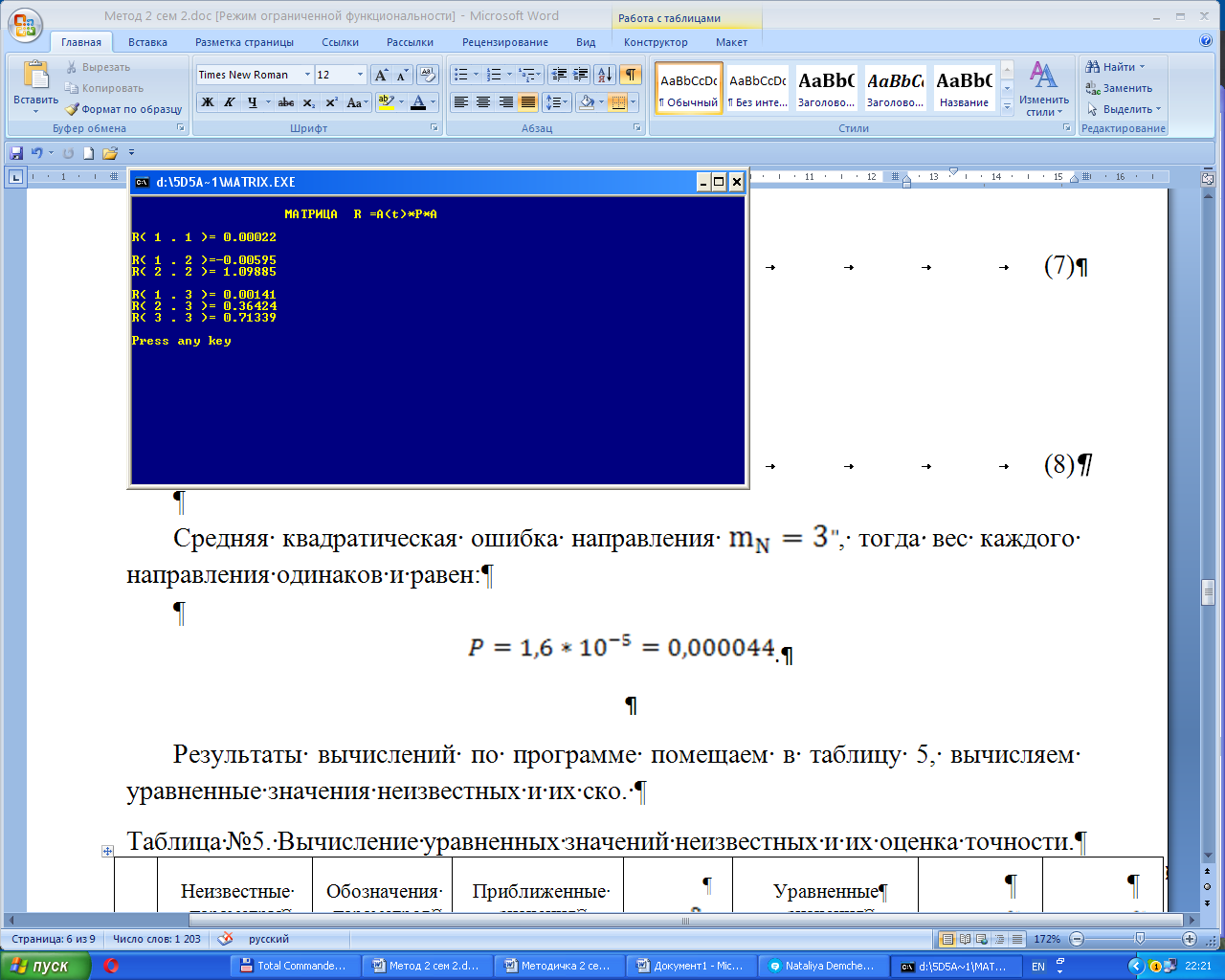
Рис. 12 - Матрица коэффициентов нормальных уравнений
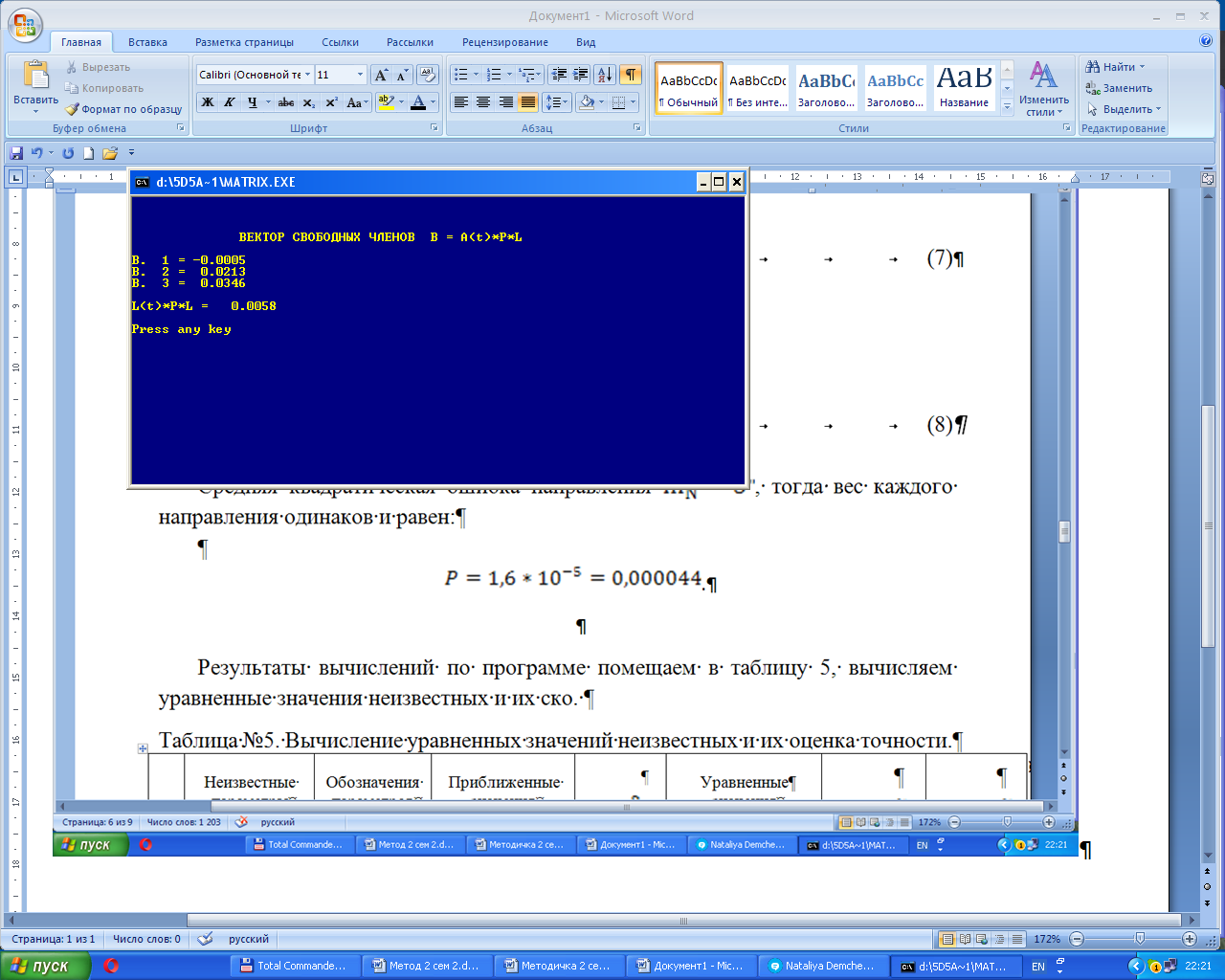
Рис. 13 - Вектор свободных членов уравнений поправок
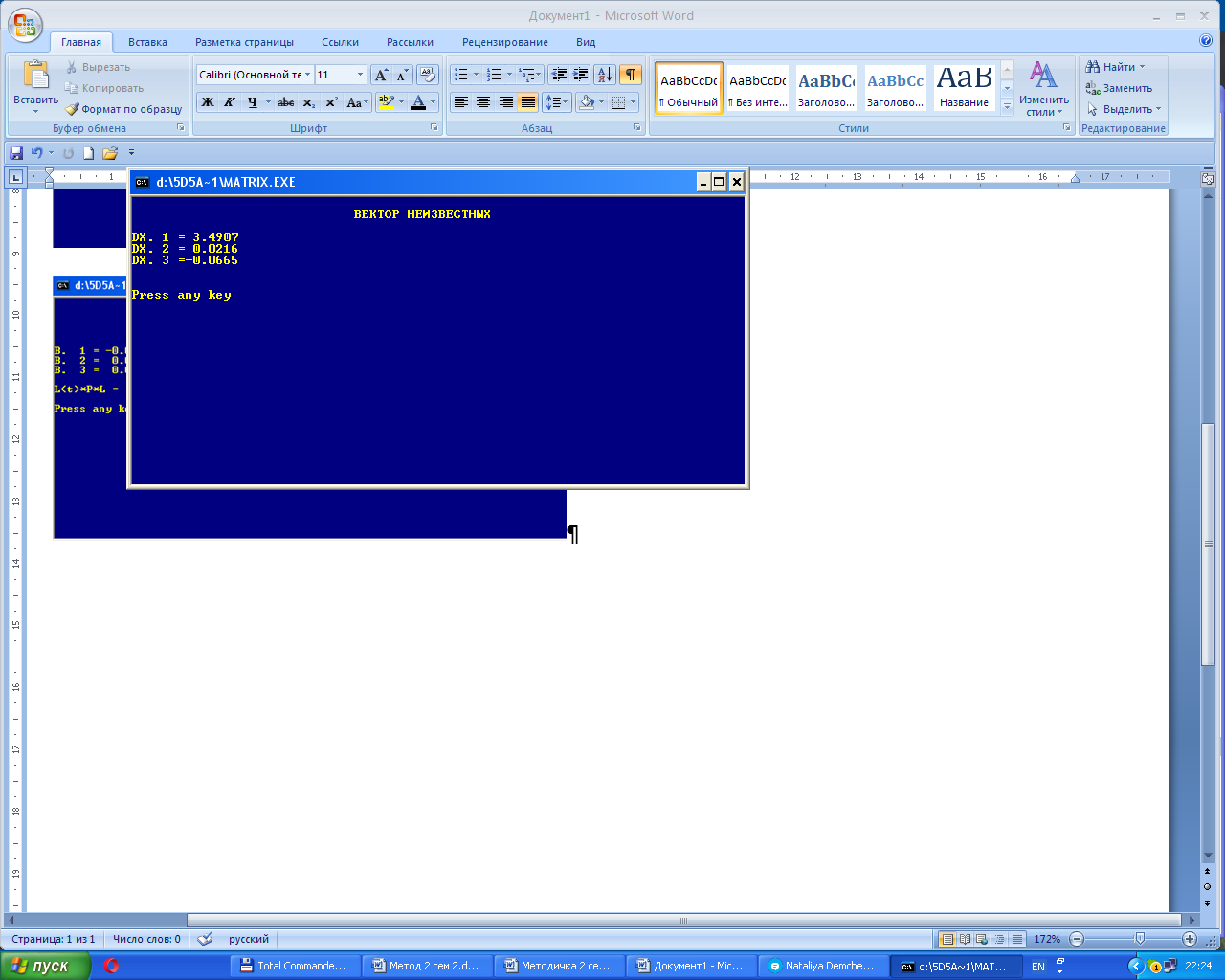
Рис. 14 -Вектор поправок к приближенным значениям неизвестных
Рис. 15 -Вектор поправок измерений
Вычисленный по любой из программ вектор решения 
и диагональные элементы матрицы обратных весов неизвестных 
() помещаем в таблицу 6, вычисляем уравненные значения неизвестных 
и их СКО 
по формулам:
(15)
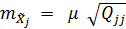, (16)
где, 
- поправка к соответствующему приближенному значению неизвестного 
, 
- диагональный элемент матрицы обратных весов неизвестных, 
- ошибка единицы веса, принятая в данной работе равной 0,02м.
Таблица №6. Вычисление уравненных значений неизвестных и их оценка точности.
| Неизвестные параметры | Обозначения параметров | Приближенные значения |
| Уравненные значения |
|
|
| 
| 291˚17'00,5" | 3,4907 | 292˚17'04,0" | 5935,836 | 1,5" |
|
| 
| 6048,222 | 0.0216 | 6048,2436 | 1,4123 | 3,8мм |
| 
| 12437,843 | -0,0665 | 12437,7765 | 1,8811 | 4,4мм |
При оформлении работы следует привести все результаты вычислений по выбранной программе в виде скриншотов экрана с нужными комментариями.
7.Выполним контроль уравнительных вычислений.
Контроль уравнительных вычислений выполним при помощи уравненных направлений, которые определим дважды. Первое уравненное значение получим по формуле:
(17)
где V – поправка к измеренному значению.
Второе уравненное значение получим по формуле:
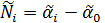(18)
где 
- уравненное значение дирекционного угла направления P- i,
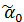- уравненное значение ориентирующего угла (таблица 6).
Уравненные дирекционные углы получают по уравненным координатам определяемого пункта по формуле:
(19)
Уравненные направления, вычисленные по формулам (16) и (17) должны сойтись в пределах ошибки округления, допустимые расхождения 0,1 секунды.
Поправки к измеренным значениям направлений можно получить по формуле:
, (20)
используя коэффициенты уравнения поправок из таблицы 3. Можно также вычислить матрицу поправок по формуле:
, (21)
например, в ECXEL. Вычисленные поправки помещаем в таблицу 8 и вычисляем уравненные направления.
Пример вычисления уравненных дирекционных углов приведен в таблице 7.
Уравненные дирекционные углы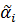 
так же можно получить по программе MATRIX.exe аналогично тому, как вычисляли приближенные значения этих дирекционных углов. Единственное отличие - вместо приближенных координат определяемого пункта под номером один следует ввести уравненные координаты пункта 
, 
.
Таблица 7 Вычисление уравненных дирекционных углов
| Элемент сети | Номер пункта | ||||
| Уi | 10021.897 | 11982.156 | 14591.085 | 14038.842 | 13471.423 |
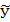
| 12437,7765 | ||||
| Уi - Y(0) | -2415.880 | -455.621 | 2153.308 | 1601.065 | 1033.646 |
| Xi | 7038.259 | 8931.452 | 8089.743 | 5647.209 | 4201.839 |
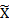
| 6048,2436 | ||||
| Xi - X(0) | 990.015 | 2883.208 | 2041.499 | -401.035 | -1846.405 |
| αi(0) | 292˚17'00,9" | 351˚01'12,2" | 46˚31'36,5 | 104˚03'43.6" | 150˚45'33,2" |
Для выполнения окончательного контроля уравнивания по полученным второй раз уравненным направлениям вычислим уравненные значения свободных членов уравнения поправок:
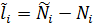(22)
Контролем будет выполнение равенства: 
. Контрольные вычисления представлены в таблице 8. Как видно, расхождения не превышают одной десятой секунды, то есть, контроль выполняется.
Таблица №8. Контроль уравнительных вычислений
| № | Измеренные направления
|
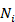
| Уравненные направления
| Уравненные дирекционные углы 
| Уравненные
направления
|
|
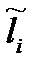
| 00˚00'00,0" | -3,1 | 359˚59'56,9" | 292˚17'00,9" | 359˚59'56,9" | -03,1" | |
| 58˚44'07,1" | 1,2 | 58˚44'08,3" | 351˚01'12,2" | 58˚44'08,2" | 1,1" | |
| 114˚14'29,6" | 3,0 | 114˚14'32,6" | 46˚31'36,5" | 114˚14'32,5" | 2,9" | |
| 171˚46'43,9" | -4,2 | 171˚46'39,7" | 104˚03'43.6" | 171˚46'39,6" | -4,3" | |
| 218˚28'26,1" | 3,1 | 218˚28'29,2" | 150˚45'33,2" | 218˚28'29,2" | 3,1" |
8.Оценка точности:
Оценка точности неизвестных параметров (, , ), выполнена
в таблице №5.
Оценим точность дирекционного угла и длины стороны p-3,которые следует представить в виде функции уравненных значений неизвестных
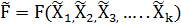(23)
Выбранные для оценки точности функции, выраженные через уравненные значения неизвестных, будут иметь вид:
; (24)
(25)
Средние квадратические ошибки функции уравненных значений неизвестных получают по формулам:
, (26)
где 
- ошибка единицы веса, 
обратный вес функции уравненных значений неизвестных.
Матрицу обратных весов функций уравненных значений неизвестных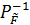 
, получают по формуле
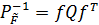, (27)
где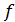 
весовая матрица размера 
, где 
- количество функций, выбранных для оценки, 
- число неизвестных; 
- матрица обратных весов неизвестных.
Каждый элемент весовой матрицы 
равен частной производной:
. (28)
Составим весовую матрицу 
размером 2х3 (две функции для оценки, три неизвестных).
; (29)
Производные можно вычислить вручную или по программе MATRIX.exe(выбрать из фрагмента вычисления уравненных дирекционных углов, относящегося к третьему исходному пункту).
Вычислим матрицу обратных весов функций уравненных неизвестных:
Из матрицы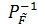 
выписываем диагональные элементы – это обратные веса функций - уравненного дирекционного угла и стороны p-3:
и вычисляем ошибку единицы веса:
.
Полученная величина ошибки единицы веса является ненадежной, так как число избыточных измерений очень мало (меньше 8), поэтому при оценке точности будем использовать величину = 0,02м, которую мы приняли при вычислении весов измерений.
Получаем средние квадратические ошибки уравненного значения стороны и дирекционного угла Р-3:
Выводы по работе
Уравненные координаты и уравненный ориентирующий угол:
;
.
Оценка точности уравненных параметров. дирекционного угла и стороны Р-3:
 =
| 1,5" |
 =
| 38 мм |
 =
| 44 мм |
 =
| 2,2" |
 =
| 18 мм |