ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
ЛЕКЦИЯ №6. Вычисление расстояния от точки до прямой в пространстве. Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью. Нахождение точки пересечения прямой и плоскости. Взаимное расположение двух прямых в пространстве. Нахождение точки пересечения двух пересекающихся прямых и расстояния между двумя параллельными или скрещивающимися прямыми.
П.1. Вычисление расстояния от точки до прямой в пространстве
Определение. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Вывод формулы.
Пусть задана прямая 
, тогда 
-направляющий вектор этой прямой; 
- точка, лежащая на
этой прямой. Из свойств векторного произведения известно, что площадь параллелограмма, построенного на векторах 
, равна модулю векторного произведения этих векторов: 
.
С другой стороны, площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне: 
. Тогда
. Получили формулу для вычисления расстояния от точки до прямой в пространстве:
Пример.
Найти расстояние между точкой M(0, 2, 3) и прямой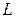 
, где
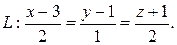
Решение. Из уравнения прямой получим: 
= {2; 1; 2} - направляющий вектор прямой; M1(3; 1; -1) - точка лежащая на прямой.
Тогда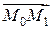 
= (3 - 0; 1 - 2; -1 – 3) = (3; -1; -4),
= 
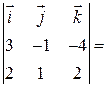i ((-1)·2 - (-4)·1) - j (3·2 - (-4)·2) + k (3·1 -(-1)·2) =
=(2; -14; 5).
.
Ответ: расстояние от точки до прямой равно 5.
п.2. Взаимное расположение прямой и плоскости.
Взаимное расположение прямой и плоскости в пространстве допускает три случая.
1) Прямая и плоскость могут пересекаться в одной точке.
2) Прямая и плоскость могут быть параллельны.
3) Прямая может лежать в плоскости.
Выяснение конкретной ситуации для прямой и плоскости зависит от способа их описания.
Предположим, что плоскость Q задана общим уравнением
Q: Ax + By + Cz + D = 0, а прямая L — каноническими уравнениями 
Уравнения прямой дают координаты точки 
на прямой и координаты направляющего вектора этой прямой, а уравнение плоскости — координаты ее нормального вектора 
Если прямая L и плоскость Q пересекаются, то направляющий вектор прямой не параллелен плоскости Q. Значит, нормальный вектор 
плоскости не ортогонален вектору , т.е. их скалярное произведение не равно нулю или 
.
Если прямая и плоскость параллельны или прямая лежит в плоскости, то выполняется условие 
Чтобы разделить случаи параллельны“ и прямая принадлежит плоскости“, нужно проверить, принадлежит ли точка прямой данной плоскости.
Таким образом, все три случая взаимного расположения прямой и
плоскости разделяются путем проверки соответствующих условий:
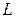принадлежит Q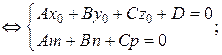 
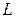параллельна Q 
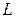пересекается с Q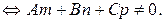 
Если прямая L задана своими общими уравнениями:
то проанализировать взаимное расположение прямой и плоскости можно следующим образом. Из общих уравнений прямой и общего уравнения плоскости составим систему трех линейных уравнений с тремя неизвестными: 
(
)
Если эта система не имеет решений, то прямая параллельна плоскости. Если она имеет единственное решение, то прямая и плоскость пересекаются в единственной точке. Последнее утверждение равносильно тому, что определитель системы отличен от нуля, т.е.
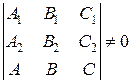
Если система 
имеет бесконечно много решений, то прямая принадлежит плоскости.