| Цель изучения: | усвоить учебные элементы на уровне знаний и умения применять их для выдвижения гипотезы и проверки гипотезы о законе распределения случайной величины. |
Учебные вопросы:
1. Статистическая гипотеза. Нулевая гипотеза. Ошибки первого и второго рода. Статистический критерий.
2. Критерий Пирсона.
Краткие сведения из теории
I. Статистической называется гипотеза о виде неизвестного распределения, или о параметрах известного распределения.
Нулевой (основной) называют выдвинутую гипотезу 
.
Конкурирующей (альтернативно) называют гипотезу 
, которая противоречит основной.
Гипотезы бывают:
1) простые;
2) сложные.
Ошибка первого рода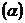 
состоит в том, что отвергается правильная нулевая гипотеза.
Ошибка второго рода 
состоит в том, что принимается неправильная нулевая гипотеза.
Статистическим критерием (критерием, критерием согласия) называют случайную величину, которая служит для проверки гипотезы.
II. Критерий согласия Пирсона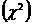 
– наиболее часто употребляемый критерий для проверки простой гипотезы о законе распределения, читается «хи квадрат».
Правило проверки гипотезы по критерию Пирсона о законе распределения случайной величины:
1) Эмпирическое распределение задано в виде последовательности равно отстоящих вариант и соответствующих им частот и задан уровень значимости 
.
| 
| 
| … | 
|
| 
| 
| … | 
|
2) Вычисляем по формулам 
, 
и 
соответственно выборочную среднюю 
и выборочное среднее квадратическое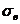 
.
3) Вычисляем теоретические частоты,
 ,
|
|
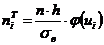где – объем выборки (находим по формуле 
);
– шаг (разность между двумя соседними вариантами);
 ,  .
|
|
Значение функции 
находим по таблице Приложений №1, причем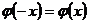 
, т.е. функция является четной.
4) Сравниваем эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:
А) составляют расчетную таблицу 4.1.,
Расчетная таблица 4.1.
| 
| 
| 
| 
| 
|
|
| |||||
|
| |||||
| … | |||||
|
| ||||
|
|
| 
|
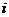
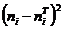
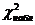
по которой находят наблюдаемое значение критерия
 .
|
|
Б) по таблице Приложений №2 критических точек распределения 
, по заданному уровню значимости и числу степеней свободы
 ,
| 
|
где 
– число групп выборки,
– число параметров предполагаемого распределения (для нормального распределения 
),
находят критическую точку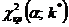 
правосторонней критической области.
5) Делаем вывод. Если 
, то нет основания отвергать гипотезу о нормальном распределении генеральной совокупности. Если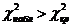 
, то гипотезу отвергают.
Задача 4.6. Выборка задана в виде распределения частот:
|
| ||||
|
|
Проверить гипотезу о нормальном распределении случайной величины по критерию Пирсона.
Решение. 1) По формуле найдем объем выборки:
.
Находим шаг 
.
2) Для нахождения выборочной средней воспользуемся формулой :
.
Выборочную дисперсию и среднее квадратическое отклонение находим по формулам и соответственно:
,
.
3) Вычисляем относительные частоты по формуле и таблице Приложений №1, но для начала рассчитаем величину 
:
.
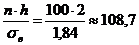Тогда
 ;
|  ;
|
 ;
|  ;
|
 ;
|  ;
|
 ;
|  .
|
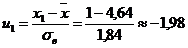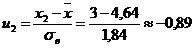4) Сравниваем эмпирические и теоретические частоты и находим 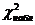по формуле . Для удобства расчетов воспользуемся таблицей 4.1.
Таблица 4.1
|
|
|
|
|
|
|
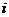
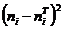
| 6,11 | 4,89 | 23,91 | 3,91 | ||
| 29,19 | -9,19 | 84,46 | 2,89 | ||
| 42,50 | 2,5 | 6,25 | 0,15 | ||
| 19,11 | 4,89 | 23,91 | 1,25 | ||
|
|  100
| 
|
Найдем число степеней свободы по формуле : с учетом 
.
По таблице Приложений №2 находим 
.
5) Так как 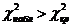(8,2>3,8), то гипотезу о нормальном распределении случайной величины отвергаем, т.е. эмпирические и теоретические частоты различаются значимо.
Ответ. Гипотезу о нормальном распределении отвергаем.
Задание для самостоятельной работы
Задача 4.7. Выборка задана в виде распределения частот:
|
| -3 | ||||
|
|
Проверить гипотезу о нормальном распределении случайной величины по критерию Пирсона.