МАТЕМАТИКА
Функции бывают нескольких видов:
1) замкнутая, ограниченная (рис. 1);
2) замкнутая, неограниченная (рис. 2);
3) незамкнутая, ограниченная (рис. 3);
4) незамкнутая, неограниченная (рис. 4).
ПЕРВАЯ ПРОИЗВОДНАЯ
В функциях двух переменных f (x;y) первая производная находится и относительно x, и относительно y. Это означает, что в первом случае мы представляем y константой (иначе говоря, некоторым коэффициентом):
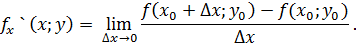
Во втором случае мы, наоборот, представляем x константой (некоторым числом, коэффициентом) и находим производную относительно y:
Первая производная находится так же, как и функциях с одной переменной, но важно помнить, что если мы находим производную по одной переменной, то вторую представляем константой*
Функции первых частных производных:
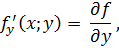
где 
— обозначение производной.
Если необходимо найти производные в определённой точке, то вместо x и y нужно подставить координаты данной точки.
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ И ГРАДИЕНТ
Существует 3 способа нахождения производной по направлению в некоторой точке A(x0; y0). В первом случае мы заранее знаем координаты вектора 
. Тогда производная по направлению находится по следующей формуле:
где v1 — первая координата вектора ,
v2 — вторая координата вектора ,
— модуль вектора , найденный по формуле: 
Если же в задаче дан некоторый угол α и нам необходимо найти производную по направлению, то следует использовать следующую формулу:
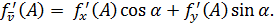
Третий способ подразумевает нахождение производной по направлению через градиент:
Формула производной в таком случае выглядит так:
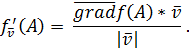
ВТОРЫЕ ПРОИЗВОДНЫЕ
Формулы вторых производных:
Алгоритм нахождения второй производной совпадает с алгоритмом нахождения первой производной для функции 2-х переменных, т.е. если мы ищем вторую производную относительно одной переменной, то другую представляем константой.
Важно отметить, что вторые производные 
и 
совпадают.
I и II ДИФФЕРЕНЦИАЛ
Первый дифференциал находится по формуле:
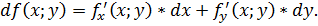
Формула второго дифференциала:
МАТРИЦА ГЁССЕ
Матрица Гёссе необходима при нахождении локальных экстремумов.
Она имеет следующий вид:
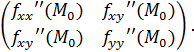
Гессиан-определитель находится следующим образом:
ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
Точка M0 называется точкой локального минимума, если для всех близких точек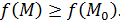 
Точка M0 называется точкой локального максимума, если для всех близких точек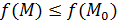 
.
Необходимое условие экстремума:
если M0 — точка локального экстремума, то:
Достаточное условие экстремума:
1) Если 
, 
, 
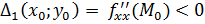— точка локального максимума.
2) Если , 
, — точка локального минимума.
ГЛОБАЛЬНЫЙ ЭКСТРЕМУМ
Для нахождения глобального экстремума функции с двумя переменными воспользуемся следующим алгоритмом.
Запишем новое уравнение:
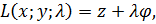где 
.
Найдём производную относительно каждой из переменных и приравняем их к нулю. Далее решим систему из полученных уравнений:
Полученные значения являются глобальными экстремумами функции.
Для того, чтобы определить, чем являются данные экстремумы: минимумом или максимумом, необходимо решить следующее уравнение.
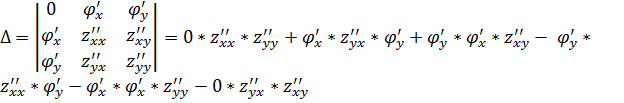
Если 
, то это точка максимума;
Если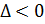 
, то это точка минимума.