Рассмотрим таблицу среднеквадратических ошибок, вычисленных по истинному значению приближаемой функции для каждого метода на конкретных примерах. Числа во втором столбце (5,15,30)- количество треугольников, по которым построена RBF-функция, δ – амплитуда ошибки, L-количество точек.
Таблица 1.
| Sin(x), L=30 | Sin(4x), L=30 | Sin(x)+Sin(4x)/4, L=30 | Sin(x)+Sin(4x)/4, L=200 | |||||
| δ | 0.2 | 0.5 | 0.3 | 0.5 | 0.3 | |||
| методд | 0.02 | 0.026 | 0.16 | 0.03 | 0.04 | 0.04 | 0.05 | |
| 0.006 | 0.03 | 0.1 | 0.003 | 0.01 | 0.08 | 0.03 | ||
| 0.006 | 0.02 | 0.05 | 0.006 | 0.02 | 0.06 | 0.009 | ||
| метод | 0.006 | 0.026 | 0.41 | 0.03 | 0.048 | 0.053 | 0.02 | |
| 0.006 | 0.026 | 0.33 | 0.03 | 0.046 | 0.053 | 0.017 | ||
| 0.006 | 0.026 | 0.2 | 0.03 | 0.046 | 0.053 | 0.017 | ||
| метод | 0.005 | 0.01 | 0.06 | 0.01 | 0.02 | 0.1 | 0.05 | |
| 0.006 | 0.05 | 0.05 | 0.004 | 0.16 | 0.026 | 0.02 | ||
| 0.007 | 0.056 | 0.03 | 0.003 | 0.02 | 0.023 | 0.04 | ||
| метод | 0.007 | 0.053 | 0.084 | 0.025 | 0.063 | 0.03 | 0.029 | |
| 0.007 | 0.053 | 0.06 | 0.025 | 0.02 | 0.03 | 0.027 | ||
| 0.007 | 0.053 | 0.06 | 0.025 | 0.02 | 0.03 | 0.027 |
Формула для вычисления ошибок по выборке:  2 , где
2 , где  и
и  -координаты
-координаты 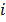 -й точки выборки.
-й точки выборки.
Формула для вычисления ошибок по истинному значению: 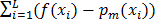 2 , где
2 , где  -истинная функция,
-истинная функция,  - функция, равная сумме треугольных функций на m-ом шаге.
- функция, равная сумме треугольных функций на m-ом шаге.
Формула для вычисления среднеквадратической ошибок по истинному значению получается из предыдущей формулы делением на количество используемых точек  .
.
По таблице видно, что результаты во многих методах неоднозначны, однако наименьшая среднеквадратическая ошибка по истинному значению функции, наблюдаемая в результате метода 3, всегда остается одной из минимальных. Так же можно заметить, что при увеличении числа экспериментальных точек, при относительно небольшом разбросе, ошибка при разных количествах треугольников в разных методах может, как и уменьшается, так и увеличиваться. К примеру, в методе 1 минимальная ошибка будет такой же, но достигаться будет при 30, а не 15 треугольниках.
Рассмотрим графики полученных ошибок по выборке и графики ошибок по истинному значению (ось X-номера треугольников, ось Y-соответствующие ошибки).
Вначале проанализируем случаи, для которых лучше работает не только 3ий метод. Рассмотрим sin(x) c разбросом 0.5 (из таблицы видно, что для него лучше подходят методы 1 и 3)
Алгоритм 3:
Рис.12 графики ошибки по выборке (темно-серая) и по истинному значению (серая)
Алгоритм 1:
Рис.13 графики ошибки по выборке (темно-серая) и по истинному значению (серая)
Во-первых, следует отметить, что ошибки по истинному значению функции ниже, чем по выборке, что говорит о хороших сглаживающих качествах нейронной сети и о возможности использовать ошибку по выборке как индикатор ошибки по истинному значению. Во-втрых, ошибка по истинному значению меньше при работе 3-го алгоритма, чем 1-го для  , дальше она начинает возрастать. Этой тенденции не видно по ошибке по выборке, но она после седьмого и восьмого шагов начинает колебаться и убывает очень медленно, что говорит о нецелесообразности добавления новых функций. То же можно сказать и про первый алгоритм после пятого шага.
, дальше она начинает возрастать. Этой тенденции не видно по ошибке по выборке, но она после седьмого и восьмого шагов начинает колебаться и убывает очень медленно, что говорит о нецелесообразности добавления новых функций. То же можно сказать и про первый алгоритм после пятого шага.
Рассмотрим функцию sin(x)+sin(4x)/4 с разброс 0.5. Это ещё один спорный случай из таблицы 1, проанализируем его, используя методы 3 и 4. Алгоритм 3:
Рис.14 графики ошибки по выборке (темно-серая) и по истинному значению (серая) при работе третьего алгоритма
Метод 4:
Рис.15 графики ошибки по выборке (темно-серая) и по истинному значению (серая) при работе четвёртого алгоритма
При работе четвёртого алгоритма минимальная ошибка достигается после трёх шагов и дальше не изменяется. При работе третьего алгоритма ошибки по выборке и по истинному значению будет меньше, чем при работе четвёртого алгоритма, но она будет достигаться на 18 шаге. В этом случае оба алгоритма работают достаточно эффективно, алгоритм 3 точнее показывает полученную зависимость, но потребует больших расчетов, чем алгоритм 4. Следует заметить, что данные алгоритмы целесообразно применять для достаточно сложных целевых функций, для которых первый алгоритм оказывается недостаточно эффективным.
Проанализируем подробнее работу 3 алгоритма.
Возьмем функцию sin(x)+sin(4x)/4 без разброса.
Рис.16 графики ошибки по выборке (темно-серая) и по истинному значению (серая)
В данном случае работу алгоритма можно закончить после 8 шагов, причём ошибка по выборке является достаточно хорошим индикатором необходимости прервать его работу. Аналогичные выводы можно сделать и для других численных экспериментов:
1) Алгоритм целесообразно применять для заметно меньшего числа шагов, чем число точек выборки.
2) Резкое замедление убывания ошибки по выборке является хорошим критерием окончания работы алгоритма.
3) Дальнейшее продолжение работы алгоритма целесообразно, если предполагается доучивание получившейся нейронной сети, а погрешность измерений (наблюдений) намного меньше достигнутого среднеквадратичного отклонения.
Можно сделать общий вывод, что третий алгоритм лучше всего приближает нашу функцию, но в случаях с большим разбросом можно также воспользоваться алгоритмами 1 и 4, причём приведённые выше выводы справедливы и для них. Целесообразность применения алгоритма 1 вытекает из его существенно меньшей трудоёмкости, в особенности это актуально при обработке данных в режиме реального времени. Алгоритм 3 является более универсальным в случае ограниченности данных и достаточных вычислительных ресурсов, так как он работает для всех случаев достаточно точно.
Заметим, что изученные алгоритмы достаточно легко распространяются на многомерный случай.
Благодарность: Статья подготовлена по результатам исследования, выполненного при финансовой поддержке гранта Российского Научного Фонда (проект 14-38-00009) «Программно-целевое управление комплексным развитием Арктической зоны РФ (Санкт-Петербургский политехнический университет Петра Великого).
Литература
1. Бастенс Д.Э., Ван ден Берг, Вуд Д. Нейронные сети и финансовые рынки: принятие решений в торговых операциях. – М: ТВП, 1998. – 236с.
2. Васильев А.Н., Тархов Д.А.– Нейросетевое моделирование. Принципы. Алгоритмы. Приложения. – СПб.:Изд-во Политехн. Ун-та. 2009. - 528 с.
3. Тархов Д.А. Нейросетевые модели и алгоритмы. – М.: Радиотехника, 2014. – 352 с.
4. Vasilyev A.N., Tarkhov D.A. Mathematical Models of Complex Systems on the Basis of Artificial Neural Networks// Nonlinear Phenomena in Complex Systems. - vol. 17, no.3, pp. 327-335 (2014).
5. N. U. Kainov, D. A. Tarkhov, T. A. Shemyakina. Application of Neural Network Modeling to Identification and Prediction Problems in Ecology Data Analysis for Metallurgy and Welding Industry// Nonlinear Phenomena in Complex Systems. vol. 17, no. 1, pp. 57-63 (2014).