Задача 2
1. Генеральная совокупность случайных значений, подчиняющихся нормальному закону распределения, характеризуется следующими параметрами:  ‑ генеральное среднее;
‑ генеральное среднее; 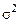 ‑ генеральная дисперсия;
‑ генеральная дисперсия;  – генеральное стандартное отклонение.
– генеральное стандартное отклонение.
2. Для оценки генеральных параметров можно использовать выборочные параметры. Выборка объёмом  , состоящая из
, состоящая из  случайных величин:
случайных величин:  (
( ), характеризуется следующими параметрами: выборочное среднее
), характеризуется следующими параметрами: выборочное среднее 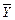 ; выборочная дисперсия
; выборочная дисперсия  ; выборочное стандартное отклонение
; выборочное стандартное отклонение 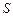 ; число степеней свободы
; число степеней свободы  выборочной дисперсии и выборочного стандартного отклонения
выборочной дисперсии и выборочного стандартного отклонения
 ;
;  ;
;
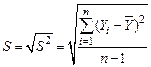 ;
; 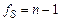 .
.
3. Проверка случайных значений выборки  на промах по критерию Смирнова – Граббса:
на промах по критерию Смирнова – Граббса:
‑ экспериментальное значение критерия Смирнова – Граббса 
 ,
,
где в качестве  выбирается такое значение выборки, которое «убежало» от выборочного среднего
выбирается такое значение выборки, которое «убежало» от выборочного среднего 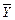 на максимальное расстояние, или такое значение выборки, для которого
на максимальное расстояние, или такое значение выборки, для которого  ;
;
‑ табличное значение критерия Смирнова – Граббса  при числе степеней свободы
при числе степеней свободы  и доверительной вероятности
и доверительной вероятности  ;
;
‑ выполнение неравенства
 (25)
(25)
означает, что в выборке  с вероятностью не менее 95 % промаха нет;
с вероятностью не менее 95 % промаха нет;
‑ выполнение неравенства
 (26)
(26)
означает, что в выборке  значение
значение  , для которого
, для которого  , является промахом.
, является промахом.
Если в выборке обнаружен промах, то его следует исключить, а оставшиеся случайные значения выборки подвергнуть повторной проверке на промах.
4. Проверка случайных значений выборки  на принадлежность их к нормальному закону распределения по критерию среднего абсолютного отклонения (САО):
на принадлежность их к нормальному закону распределения по критерию среднего абсолютного отклонения (САО):
‑ экспериментальное значения  критерия САО
критерия САО
 ;
;
‑ табличное значения  критерия САО при доверительной вероятности
критерия САО при доверительной вероятности  равно
равно
 ;
;
‑ выполнение неравенства

означает, что случайные значения выборки  с вероятностью не менее 95 %принадлежат к нормальному закону распределения;
с вероятностью не менее 95 %принадлежат к нормальному закону распределения;
‑ выполнение неравенства
 (30)
(30)
означает, что случайные значения выборки  не принадлежат к нормальному закону распределения.
не принадлежат к нормальному закону распределения.
NB! Если случайные значения выборки не подчиняются нормальному закону распределения, то её выборочные параметры не могут быть использованы для оценки параметров генеральной совокупности с помощью тех формул, которые будут приведены ниже.
Если в выборке нет промахов, а её значения подчиняются нормальному закону распределения, то такая выборка будем называть очищенной. Параметры очищенной выборки можно использовать для оценки параметров генеральной совокупности.
5. Оценка генерального среднего по выборочным параметрам очищенной выборки:
‑ абсолютная ошибка  генерального среднего
генерального среднего 
 ,
,
где  ‑ значение критерия Стьюдента при числе степеней свободы
‑ значение критерия Стьюдента при числе степеней свободы 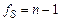 и доверительной вероятности
и доверительной вероятности  ;
;
‑ доверительный интервал генерального среднего  с доверительной вероятностью
с доверительной вероятностью  равен
равен
 , где
, где  ,
,  .
.
6. Оценка генерального стандартного отклонения  по выборочным параметрам очищенной выборки:
по выборочным параметрам очищенной выборки:
‑ доверительный интервал генерального стандартного отклонения  с доверительной вероятностью
с доверительной вероятностью 
 , где
, где  ,
,  ,
,
где 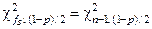 и
и  ‑ нижнее и верхнее табличные значения критерия Пирсона с числом степеней свободы
‑ нижнее и верхнее табличные значения критерия Пирсона с числом степеней свободы 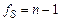 и доверительной вероятности
и доверительной вероятности  .
.
Формулировка задачи. На предприятии изготавливают антифрикционные втулки методом порошковой металлургии (прессование и спекание смеси порошков железа, меди и олова). Качество изготовленных втулок оценивается пределом прочности при растяжении.
Изготовленные втулки поступают в отдел технического контроля партиями в коробках по 1000 шт. Контроль качества производственной партии ведется выборочным методом. Из коробки случайным образом извлекается n втулок, проводится испытание их на прочность с последующей статистической обработкой полученных результатов. По результатам расчетов необходимо сделать заключение о годности данной партии втулок.
Математическая постановка задачи:
1) на основе выборочных значений прочности (481, 452, 447, 437, 463, 401, 485, 469, 468, 476, 459) МПа рассчитать доверительный интервал генерального среднего  и доверительный интервал генерального стандартного отклонения
и доверительный интервал генерального стандартного отклонения  ;
;
2) принять решение о годности партии втулок в количестве 1000 шт. В качестве критерия годности партии втулок принимается следующее выражение:  , где
, где 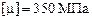 . В противном случае партию втулок в количестве 1000 шт. следует признать негодной.
. В противном случае партию втулок в количестве 1000 шт. следует признать негодной.
План решения задачи
1. Внимательно прочитать условия задачи.
2. Провести предварительную обработку экспериментальных данных исходной выборки методами математической статистики (расчёт выборочных параметров, проверка случайных значений исходной выборки на промах и на принадлежность их к нормальному закону распределения, если нет промаха).
3. Провести предварительную обработку экспериментальных данных очищенной выборки методами математической статистики (расчёт выборочных параметров, проверка случайных значений очищенной выборки на промах и на принадлежность их к нормальному закону распределения).
4. Оценить параметры генеральной дисперсии по выборочным параметрам очищенной выборки.
5. По принятому критерию качества  принять решение о годности партии втулок в количестве 1000 шт.
принять решение о годности партии втулок в количестве 1000 шт.
NB! Все промежуточные расчеты производить с точностью не менее 4-х значащих цифр.
Решение задачи плану
1. Пункт 1 выполнить самостоятельно.
2. Для и сходной выборки объемом  (481, 452, 447, 437, 463, 401, 485, 469, 468, 476, 459) МПа рассчитаем выборочные параметры:
(481, 452, 447, 437, 463, 401, 485, 469, 468, 476, 459) МПа рассчитаем выборочные параметры:
‑ выборочное среднее исходной выборки 

‑ выборочная дисперсия исходной выборки 

 ‑ выборочное стандартное отклонение исходной выборки
‑ выборочное стандартное отклонение исходной выборки 
 ;
;
‑ число степеней свободы  выборочной дисперсии
выборочной дисперсии  исходной выборки
исходной выборки
 .
.
Проверим случайные значения исходной выборки объемом  на промах по критерию Смирнова – Граббса:
на промах по критерию Смирнова – Граббса:
‑ найдем случайное значение исходной выборки  , которое «убежало» от выборочного среднего
, которое «убежало» от выборочного среднего  на максимальное расстояние, то есть найдем такое
на максимальное расстояние, то есть найдем такое  , для которого разность
, для которого разность  . Очевидно, что таким свойством обладает либо самое большое значение выборки
. Очевидно, что таким свойством обладает либо самое большое значение выборки  , либо самое маленькое –
, либо самое маленькое –  . Так как
. Так как  >
>  , то на промах проверим
, то на промах проверим  :
:
‑ экспериментальное значение критерия Смирнова – Граббса для 
 ;
;
‑ табличное значение критерия Смирнова – Граббса  при числе степеней свободы
при числе степеней свободы 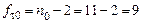 и доверительной вероятности
и доверительной вероятности 
 .
.
Вывод: в исходной выборке случайная величина Y 6 = 401 является промахом, так как  Проверку случайных значений выборки А на принадлежность их к нормальному закону распределения проводить не имеет смысла, пока не исключён промах.
Проверку случайных значений выборки А на принадлежность их к нормальному закону распределения проводить не имеет смысла, пока не исключён промах.
После исключения промаха из исходной выборки рассчитаем выборочные параметры обновленной выборки объемом  (481, 452, 447, 437, 463, 485, 469, 468, 476, 459) МПа:
(481, 452, 447, 437, 463, 485, 469, 468, 476, 459) МПа:
‑ выборочное среднее обновленной выборки 

‑ выборочная дисперсия обновленной выборки 


‑ выборочное стандартное отклонение обновленной выборки 
 ;
;
‑ число степеней свободы  выборочной дисперсии
выборочной дисперсии  обновленной выборки
обновленной выборки
 .
.
Проверим случайные значения обновленной выборки объемом n 1 = 10 на промах по критерию Смирнова – Граббса:
‑ найдем случайное значение выборки  , которое «убежало» от выборочного среднего
, которое «убежало» от выборочного среднего  на максимальное расстояние, то есть найдем такое
на максимальное расстояние, то есть найдем такое  , для которого разность
, для которого разность 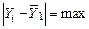 . Очевидно, что таким свойством обладает либо самое большое значение выборки
. Очевидно, что таким свойством обладает либо самое большое значение выборки  , либо самое маленькое –
, либо самое маленькое – 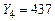 . Так как
. Так как  >
>  , то на промах проверим
, то на промах проверим 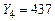 ;
;
‑ экспериментальное значение критерия Смирнова – Граббса для 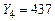
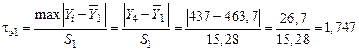 ;
;
‑ табличное значение критерия Смирнова – Граббса  при числе степеней свободы
при числе степеней свободы 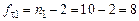 и доверительной вероятности
и доверительной вероятности 
 .
.
Вывод: в обновленной выборке объемом  с вероятностью не менее 95 % промаха нет, так как даже самое удаленное от выборочного среднего
с вероятностью не менее 95 % промаха нет, так как даже самое удаленное от выборочного среднего 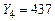 не является промахом (
не является промахом ( ).
).
Проверим случайные значения обновленной выборки объемом  на принадлежность их к нормальному закону распределения по критерию САО:
на принадлежность их к нормальному закону распределения по критерию САО:
‑ экспериментальное значения критерия САО



‑ табличное значения 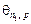 критерия САО с вероятностью
критерия САО с вероятностью 
 .
.
Вывод: случайные значения обновленной выборки объемом  с вероятностью не менее 95 % принадлежат к нормальному закону распределения, так как, так как
с вероятностью не менее 95 % принадлежат к нормальному закону распределения, так как, так как  .
.
Так как в обновленной выборке нет промахов, а ее случайные значения принадлежат к нормальному закону распределения, то обновленная выборка является очищенной выборкой объемом  .
.
4. По выборочным параметрам очищенной выборки оценим генеральные параметры.
Для очищенной выборки  рассчитаем доверительный интервал генерального среднего
рассчитаем доверительный интервал генерального среднего  по критерию Стьюдента:
по критерию Стьюдента:
‑ абсолютная ошибка 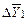 генерального среднего
генерального среднего 
 ;
;
где  ‑ табличное значение критерия Стьюдента при числе степеней свободы
‑ табличное значение критерия Стьюдента при числе степеней свободы  и доверительной вероятности
и доверительной вероятности 
 ;
;
‑ доверительный интервал генерального среднего (предел прочности при растяжении), рассчитанный по результатам очищенной выборки с доверительной вероятностью  с учётом алгоритма корректного оформления результатов расчёта
с учётом алгоритма корректного оформления результатов расчёта
 , или
, или  ,
,
где
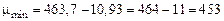 ;
;
 .
.
Вывод: для очищенной выборки генеральное среднее с вероятностью 95 % находится в интервале  .
.
Для очищенной выборки объемом  рассчитаем доверительный интервал генерального стандартного отклонения
рассчитаем доверительный интервал генерального стандартного отклонения  по критерию Пирсона
по критерию Пирсона
 , или
, или 
где
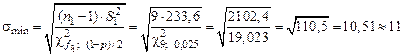 ,
,
 ,
,
где нижнее и верхнее табличные значения критерия Пирсона 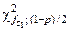 и
и  с числом степеней свободы
с числом степеней свободы  и доверительной вероятности
и доверительной вероятности 
 ;
;
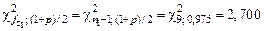 .
.
Вывод: для очищенной выборки генеральное стандартное отклонение с вероятностью 95 % находится в интервале  .
.
5. По выбранному критерию качества втулок  примем решение о годности партии втулок в количестве 1000 шт. Выполнение равенства
примем решение о годности партии втулок в количестве 1000 шт. Выполнение равенства
 .
.
говорит о том, что партию втулок в количестве 1000 шт. с вероятностью не менее 95 % следует считать годной.
Ответ: 1) Параметры исходной выборки:  ;
; 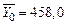 ;
;  ;
;  ;
;  . Значение
. Значение  ‑ промах, так как
‑ промах, так как 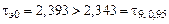 .
.
2) Параметры обновленной выборки:  ;
;  ;
;  ;
;  ;
;  . В выборке промахов нет, так как
. В выборке промахов нет, так как  . Случайные значения обновленной (очищенной) выборки подчиняются нормальному закону распределения, так как
. Случайные значения обновленной (очищенной) выборки подчиняются нормальному закону распределения, так как 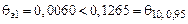 .
.
3) Доверительные интервалы генерального среднего и генерального стандартного отклонения с вероятностью не менее 95 % равны
 ,
,
 .
.
4) Статистический контроль показал, что партию втулок в количестве 1000 шт. с вероятностью не менее 95 %следует считать годной, так как  .
.
Контрольные вопросы
1. Напишите формулу для расчета выборочного среднего.
2. Напишите формулу для расчета выборочной дисперсии и её числа степеней свободы.
3. Сформулируйте алгоритм проверки случайных значений выборки на промах по критерию Смирнова ‑ Граббса.
4. Сформулируйте алгоритм принадлежности случайных значений выборки к нормальному закону распределения по критерию САО.
5. Сформулируйте алгоритм расчёта доверительного интервала генерального среднего по критерию Стьюдента.
6. Сформулируйте алгоритм расчёта доверительного интервала генеральной дисперсии по критерию Пирсона.
Контрольные задачи
Выборочные значения предела прочности втулок при сжатии, МПа
| № обр. | Номера вариантов | ||||||||||||||

| |||||||||||||||
| № обр. | Номера вариантов | ||||||||||||||

|