Составим математическую модель задачи

Контрольная работа

по дисциплине:

«Математическое моделирование »

 

Вариант 1

 

Выполнил

студент группы б-НТТКипу31

Зачетная книжка №

ФИО

 

Проверил

Перегудов А.Б.

 

 

Саратов 2017

Задание 1

Вариант №1

Транспортная задача.
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

						Запасы
Потребности

Проверим необходимое и достаточное условие разрешимости задачи.
∑a = 200 + 175 + 225 = 600
∑b = 100 + 130 + 80 + 190 + 100 = 600
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.

 

						Запасы
Потребности

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.
Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.
Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

 

						Запасы
			4[55]	2[145]
		1[130]		1[45]
	2[100]		6[25]		7[100]
Потребности

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно:
F(x) = 4*55 + 2*145 + 1*130 + 1*45 + 2*100 + 6*25 + 7*100 = 1735
Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.
u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4
u₃ + v₃ = 6; 4 + u₃ = 6; u₃ = 2
u₃ + v₁ = 2; 2 + v₁ = 2; v₁ = 0
u₃ + v₅ = 7; 2 + v₅ = 7; v₅ = 5
u₁ + v₄ = 2; 0 + v₄ = 2; v₄ = 2
u₂ + v₄ = 1; 2 + u₂ = 1; u₂ = -1
u₂ + v₂ = 1; -1 + v₂ = 1; v₂ = 2

	v1=0	v2=2	v3=4	v4=2	v5=5
u1=0			4[55]	2[145]
u2=-1		1[130]		1[45]
u3=2	2[100]		6[25]		7[100]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij
(3;2): 2 + 2 > 3; ∆₃₂ = 2 + 2 - 3 = 1
Выбираем максимальную оценку свободной клетки (3;2): 3
Для этого в перспективную клетку (3;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

 

 

						Запасы
			4[55][+]	2[145][-]
		1[130][-]		1[45][+]
	2[100]	3[+]	6[25][-]		7[100]
Потребности

Цикл приведен в таблице (3,2 → 3,3 → 1,3 → 1,4 → 2,4 → 2,2).
Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 3) = 25. Прибавляем 25 к объемам грузов, стоящих в плюсовых клетках и вычитаем 25 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

						Запасы
			4[80]	2[120]
		1[105]		1[70]
	2[100]	3[25]			7[100]
Потребности

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.
u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4
u₁ + v₄ = 2; 0 + v₄ = 2; v₄ = 2
u₂ + v₄ = 1; 2 + u₂ = 1; u₂ = -1
u₂ + v₂ = 1; -1 + v₂ = 1; v₂ = 2
u₃ + v₂ = 3; 2 + u₃ = 3; u₃ = 1
u₃ + v₁ = 2; 1 + v₁ = 2; v₁ = 1
u₃ + v₅ = 7; 1 + v₅ = 7; v₅ = 6

 

	v1=1	v2=2	v3=4	v4=2	v5=6
u1=0			4[80]	2[120]
u2=-1		1[105]		1[70]
u3=1	2[100]	3[25]			7[100]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij
(1;5): 0 + 6 > 5; ∆₁₅ = 0 + 6 - 5 = 1
Выбираем максимальную оценку свободной клетки (1;5): 5
Для этого в перспективную клетку (1;5) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

						Запасы
			4[80]	2[120][-]	5[+]
		1[105][-]		1[70][+]
	2[100]	3[25][+]			7[100][-]
Потребности

Цикл приведен в таблице (1,5 → 1,4 → 2,4 → 2,2 → 3,2 → 3,5).
Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 5) = 100. Прибавляем 100 к объемам грузов, стоящих в плюсовых клетках и вычитаем 100 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

 

						Запасы
			4[80]	2[20]	5[100]
		1[5]		1[170]
	2[100]	3[125]
Потребности

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.
u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4
u₁ + v₄ = 2; 0 + v₄ = 2; v₄ = 2
u₂ + v₄ = 1; 2 + u₂ = 1; u₂ = -1
u₂ + v₂ = 1; -1 + v₂ = 1; v₂ = 2
u₃ + v₂ = 3; 2 + u₃ = 3; u₃ = 1
u₃ + v₁ = 2; 1 + v₁ = 2; v₁ = 1
u₁ + v₅ = 5; 0 + v₅ = 5; v₅ = 5

	v1=1	v2=2	v3=4	v4=2	v5=5
u1=0			4[80]	2[20]	5[100]
u2=-1		1[5]		1[170]
u3=1	2[100]	3[125]

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.
Минимальные затраты составят: F(x) = 4*80 + 2*20 + 5*100 + 1*5 + 1*170 + 2*100 + 3*125 = 1610
Анализ оптимального плана.
Из 1-го хранилища необходимо бензин направить на 3-ю заправочную станцию (80 тонн), в 4-ю заправочную (20 тонн), в 5-ю (100 тонн)
Из 2-го хранилища необходимо бензин направить в 2-ю заправку (5 тонн), в 4-ю (170 тонн)
Из 3-го в 1-ю (100 тонн), во 2-ю (125 тонн)

Задание 2

Найдем кратчайшее расстояние по сети от всех точек до точки с номером 1.

 

 

Номера точек, между которыми рассчитывается расстояние	Кратчайшее расстояние	Маршрут, по которому проходит кратчайшее расстояние
1-1
2-1		2-1
3-1		3-1
4-1		4-2-1
5-1		5-3-1
6-1		6-3-1
7-1		7-4-2-1
8-1		8-6-3-1
9-1		9-6-3-1
10-1		10-8-6-3-1
11-1		11-7-4-2-1
12-1		12-10-8-6-3-1

Оптимальным является путь 3-1

Задание 3

Вариант №1

Виды сырья	Запасы сырья	Расход сырья на единицу продукции
p1	p2
I
II
III
Доход от реализации единицы продукции		10

 

В соответствии с данными таблицы необходимо так организовать выпуск продукции П1 и П2, чтобы общая прибыль от реализации продукции была максимальной.

Составим математическую модель задачи

 

Найти наибольшее значение функции

 

F = 11 x₁ + 10 x₂

при следующих ограничениях:

		7 x1	+	8 x2	≤
	6 x1	+	3 x2	≤
	4 x1	+	x2	≤

x₁ ≥ 0 x₂ ≥ 0

 

Решение:

Точки, координаты которых удовлетворяют одновременно всем неравенствам системы ограничений, называются областью допустимых решений.

Рассмотрим неравенство 1 системы ограничений.

7 x₁ + 8 x₂ ≤ 50

Построим прямую: 7 x₁ + 8 x₂ = 50

Пусть x₁ =0 => 8 x₂ = 50 => x₂ = 25/4

Пусть x₂ =0 => 7 x₁ = 50 => x₁ = 50/7

Найдены координаты двух точек (0, 25/4) и (50/7,0). Соединяем их и получаем необходимую прямую. Знак неравенства ≤, следовательно, нас интересуют точки расположенные ниже построенной прямой.

Рассмотрим неравенство 2 системы ограничений.

6 x₁ + 3 x₂ ≤ 35

Построим прямую: 6 x₁ + 3 x₂ = 35

Пусть x₁ =0 => 3 x₂ = 35 => x₂ = 35/3

Пусть x₂ =0 => 6 x₁ = 35 => x₁ = 35/6

Найдены координаты двух точек (0, 35/3) и (35/6,0). Соединяем их и получаем необходимую прямую. Знак неравенства ≤, следовательно, нас интересуют точки расположенные ниже построенной прямой.

Рассмотрим неравенство 3 системы ограничений.

4 x₁ + x₂ ≤ 17

Построим прямую: 4 x₁ + x₂ = 17

Пусть x₁ =0 => x₂ = 17

Пусть x₂ =0 => 4 x₁ = 17 => x₁ = 17/4

Найдены коородинаты двух точек (0, 17) и (17/4,0). Соединяем их и получаем необходимую прямую. Знак неравенства ≤, следовательно, нас интересуют точки расположенные ниже построенной прямой (3).

В итоге получим область допустимых решений.

Строим вектор С = (11, 10), координатами которого являются коэффициенты функции F.

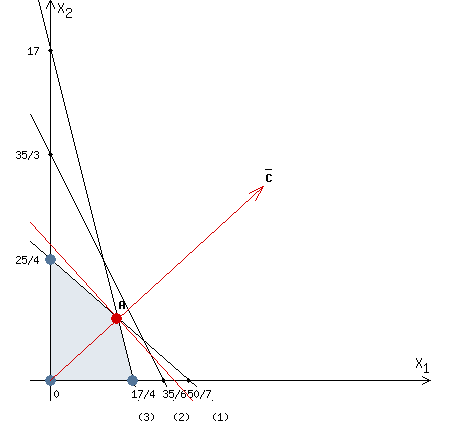
Будем перемещать "красную" прямую, перпендикулярно вектору С, от левого нижнего угла к правому верхнему.

В точке, в которой "красная" прямая в первый раз пересечет область допустимых решений, функция F достигает своего наименьшего значения.

В точке, в которой "красная" прямая в последний раз пересечет область допустимых решений, функция F достигает своего наибольшего значения.

Функция F достигает наибольшего значения в точке A.

Координаты точки А найдем из систем уравнений:

		7 x1	+	8 x2	=		=>	x1 = 86/25
	4 x1	+	x2	=		x2 = 81/25

Вычислим значение функции F в точке A (86/25,81/25).

F (A) = 11 * 86/25 + 10 * 81/25 = 1756/25

 

Ответ:

x₁ = 86/25, x₂ = 81/25

F _max = 1756/25