Пересечение множеств.
Объединение множеств.
Разность множеств
Дополнение множества
Теорема 2. Пусть A, B и C —произвольные множества. Справедливы следующие
равенства:
1. A ∪ A = A A ∩ A = A
2. Коммутативность операций ∪ и ∩
A ∪ B = B ∪ A A ∩ B = B ∩ A.
3. Ассоциативность операций ∪ и ∩
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C).
4. Дистрибутивность операций ∪ и ∩
(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).
Тема: Комбинаторика.
Правило суммы. Пусть объект a можно выбрать m способами, а объект b можно выбрать n способами, причём выбор одного объекта исключает одновременный выбор другого объекта. Тогда выбор «либо a, либо b» можно сделать m + n способами.
Правило произведения: Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то существует n*m различных пар с выбранными первым и вторым элементами.
Продемонстрируем его применение на примере.
Пример 1: Сколько различных чисел можно записать с помощью цифр 0, 2, 4, 6, 8?
В качестве первой цифры числа может быть выбрана любая из данных цифр кроме нуля. Т.е. на первое место претендуют 4 варианта цифр, n=4.
На второе место претендуют 5 цифр, т.е. m=5
Используя правило произведения, число различных двузначных чисел, составленных из предложенных цифр равно n на m, т.е. 4 умноженное на 5.
Получаем 20 различных вариантов двузначных чисел.
Пример 2: В школьной олимпиаде по математике победителями оказались 3 человека, в олимпиаде по физике – 2 человека, в олимпиаде по химии – 4 человека. На районные олимпиады по математике, физике и химии, школа должна направить по одному учащемуся из числа победителей школьных туров по трем предметам. Сколькими способами это можно сделать?
Пользуясь правилом произведения, одного участника на олимпиаду по математике и одного на олимпиаду по физике можно выбрать 3·2= 6 способами. К каждой из полученных 6 пар, можно присоединить любого из 4 победителей олимпиады по химии. Таким образом троих человек для участия в названных трёх олимпиадах можно выбрать 24 способами.
Определение: Соединения, содержащие n элементов, выбираемых из элементов m различных видов, и отличающиеся одно от другого либо составом, либо порядком следования в них элементов называется размещениями с повторениями из m по n.
- число размещений с
повторениями.
Пример 3: Сколько различных четырехбуквенных слов можно составить, пользуясь двумя буквами «м» и «а»?
На каждое место в слове претендуют 2 буквы.
Таким образом, получаем 16 различных слов, которые можно составить из букв «м» и «а».
Перестановки.
Определение: перестановками из n элементов называются соединения, которые состоят из n элементов и отличаются одно от другого только порядком их расположения.
Обозначение: 
n! – произведение первых n натуральных чисел.
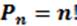– число перестановок из n различных элементов.
Задача 1: Сколькими способами можно положить 10 различных открыток в 10 имеющихся конвертов (по одной открытке в конверте)?
По формуле находим
способов разложить 10 различных открыток по конвертам.
Если некоторые переставляемые элементы будут одинаковыми, то всевозможных различных перестановок будет меньше – некоторые перестановки совпадут. Например:
Сколькими способами можно переставить буквы в слове «мама»?
МАМА
переставляя буквы в слове «мама», в котором две пары одинаковых букв, то перестановок получится 6: мама, маам, ммаа, амам, аамм, амма.
Определение: Перестановки, образованные из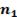 
элементов первого вида, 
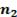элементов второго вида и так далее до 
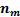элементов m-го вида
называют перестановками с повторениями.
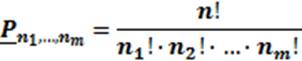
Задача 2: Сколько анаграмм можно составить из слова «макака»?
В этом слове буква
«а» - используется 3 раза
«к» - используется 2 раза
«м» - используется 1 раз
Размещения без повторений.
Определение: Размещениями без повторений из m элементов по n, где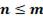 
называются такие соединения, каждое из которых содержит n элементов, взятых из данных m разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Формула:
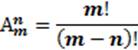
Задача: Сколько различных двузначных чисел можно записать с помощью цифр 1, 2, 3, 4 при условии, что в каждой записи нет одинаковых цифр?
Перебором можно убедится, что из данных цифр можно составить 12 двузначных чисел.
12 13 14
21 23 24
31 32 34
41 42 43
В записи двузначного числа, на первом месте может стоять любая из четырех цифр, а на втором месте любая из трех оставшихся. По правилу произведения так же получаем 4*3=12.
При решении задачи, из четырех данных элементов были образованы всевозможные соединения по два элемента в каждом, причем любые два соединения отличались друг от друга либо составом элементов, либо их расположением. Такие соединения называются размещениями.
Задача: Сколькими способами можно обозначить вершины данного треугольника, используя буквы A B C D E F?
– способов обозначить вершины треугольника.
Задача: Решите уравнение 
Обратим внимание, что 
По формуле получаем, что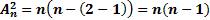 
По условию 
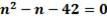
Корни: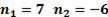 
– не подходит, т.к. корнем уравнения должно быть натуральное число
Ответ: n=7
