Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
Механизм (рис. К2, а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами Ol и О2 шарнирами.

Дано:  = 120°,
= 120°, 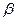 = 60°,
= 60°,  = 90°, φ = 0°,θ = 30°, AD = DE,
= 90°, φ = 0°,θ = 30°, AD = DE,  = 0,6 м,
= 0,6 м, 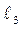 = 1,2 м, ω1 = 5с-1,
= 1,2 м, ω1 = 5с-1, 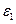 = 8 с-2.
= 8 с-2.
Определить: vB, vE, 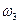 и аА.
и аА.
Решение.
1. Строим положение механизма в соответствии с заданными углами (рис. К2, б).
2. Определяем vE. Точка Е принадлежит стержню АЕ. Чтобы найти vE, надо знать скорость какой-нибудь другой точки этого стержня и направление vE. По данным задачи можем определить
vA = ω1  = 5
= 5  0,6 = 3 м/с;
0,6 = 3 м/с; 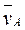
 O1А. (1)
O1А. (1)
Направление 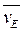 найдем, учтя, что точка Е принадлежит одновременно стержню 02Е, вращающемуся вокруг О1; следовательно,
найдем, учтя, что точка Е принадлежит одновременно стержню 02Е, вращающемуся вокруг О1; следовательно, 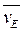
 O1Е. Теперь, зная
O1Е. Теперь, зная 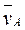 и направление
и направление 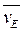 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АЕ) на прямую, соединяющую эти точки (прямая АЕ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АЕ) на прямую, соединяющую эти точки (прямая АЕ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 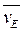 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим:
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим:
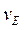 cos 60° = vA cos 30°; vE = 3 √3 = 5,2 м/с. (2)
cos 60° = vA cos 30°; vE = 3 √3 = 5,2 м/с. (2)
3. Определяем vB. Точка В принадлежит стержню BD. Чтобы определить vB, надо сначала найти скорость точки D, принадлежащей одновременно стержню АЕ. Для этого построим мгновенный центр скоростей (МЦС) стержня AE; это точка С2, лежащая на пересечении перпендикуляров к 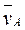 и
и 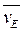 , восставленных из точек А и Е ( к
, восставленных из точек А и Е ( к 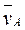 и
и 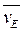 перпендикулярны стержни 1и 4 ). По направлению вектора
перпендикулярны стержни 1и 4 ). По направлению вектора 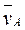 определяем направление поворота стержня АЕ вокруг МЦС С2. Вектор
определяем направление поворота стержня АЕ вокруг МЦС С2. Вектор  будет перпендикулярен отрезку C2D, соединяющему точки D и С2, и направлен в сторону поворота. Величину vD найдем из пропорции
будет перпендикулярен отрезку C2D, соединяющему точки D и С2, и направлен в сторону поворота. Величину vD найдем из пропорции

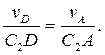 (3)
(3)
Чтобы вычислить C2D и С2А, заметим, что ∆АС2Е – прямоугольный, так как острые углы в нем равны 30 и 60°, и что СгА =АЕ sin 30° = 0,5 АЕ =AD. Тогда ∆AC2D является равносторонними С2А = C2D. В результате равенство (3) дает

Так как точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно, то направление  известно. Тогда, восставляя из точек В и D перпендикуляры к скоростям
известно. Тогда, восставляя из точек В и D перпендикуляры к скоростям  и
и  , построим МЦС C3стержня BD. По направлению вектора
, построим МЦС C3стержня BD. По направлению вектора  определяем направление поворота стержня BD вокруг центра С3. Вектор
определяем направление поворота стержня BD вокруг центра С3. Вектор  будет направлен в сторону поворота стержня BD. Из рис. К2 б видно, что
будет направлен в сторону поворота стержня BD. Из рис. К2 б видно, что 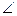 C3DB = 30°, a
C3DB = 30°, a 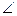 DС3B = 90°, откуда С3В = l 3 sin 30°, C3D = l 3 cos 30°. Составив теперь пропорцию, найдем что:
DС3B = 90°, откуда С3В = l 3 sin 30°, C3D = l 3 cos 30°. Составив теперь пропорцию, найдем что:
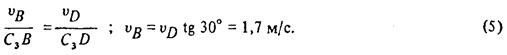
4. Определяем ω3. Так как МЦС стержня 3 известен (точка С3), то

5. Определяем aA. Так как 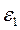 известно, то aAτ = l 1
известно, то aAτ = l 1 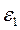 . Далее
. Далее 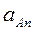 =
= 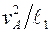 или
или 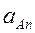 = l 1ω12 тогда
= l 1ω12 тогда  . Произведя вычисления, получаем
. Произведя вычисления, получаем 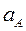 = 15,8 м/с2
= 15,8 м/с2
Ответ: vE = 5,2 м/с, vB = 1,7 м/с, ω 3 = 2,9 с-1 ,аА = 15,8 м/с2.
Задача КЗ
Прямоугольная пластина (рис. К3.0 – К3.5) или круглая пластина радиусом R = 60 см (рис. К3.6 – К3.9) вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в табл. КЗ (при знаке минус направление ω противоположно показанному на рисунке).
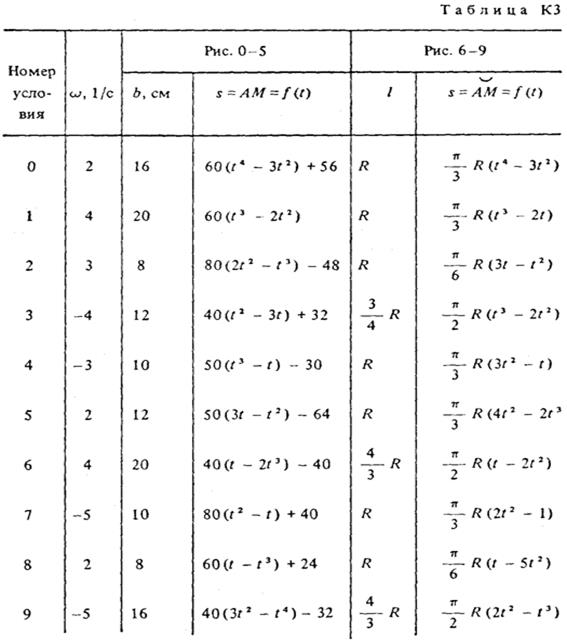
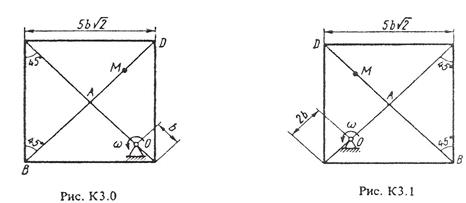
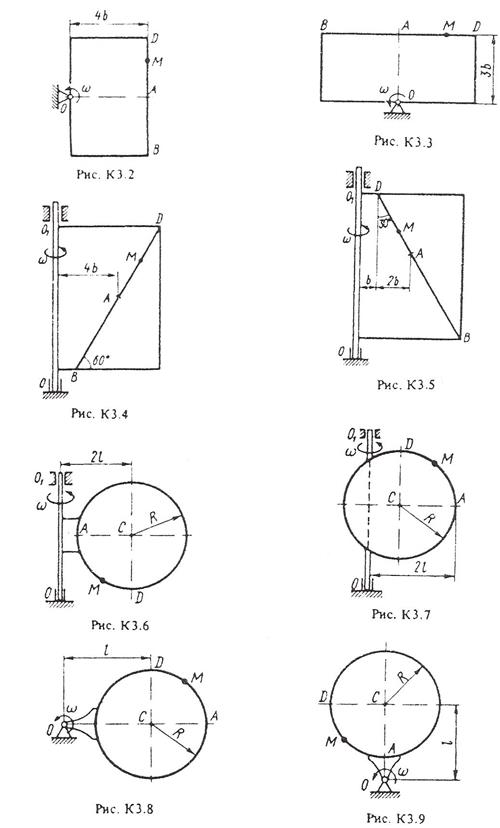
Ось вращения на рис. КЗ.0 – КЗ.З и КЗ.8, К3.9 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. К3.4 – К3.7 ось вращения ОО лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой ВD (рис. К3.0 – К3.5) или по окружности радиуса R, т.е. по ободу пластины (рис. К3.6 – К3.9), движется точка М. Закон ее относительного движения, выражаемый уравнением s = AM = f (t) (s – в сантиметрах, t – в секундах), задан в табл. КЗ отдельно для рис. К3.0 – К3.5 и для рис. К3.6 – К3.9, при этом на рис. 6 – 9 s = AM и отсчитывается по дуге окружности; там же даны размеры b и  . На всех рисунках точка М показана в положении, при котором s = AM > 0 (при s < 0 точка М находится по другую сторону от точки А).
. На всех рисунках точка М показана в положении, при котором s = AM > 0 (при s < 0 точка М находится по другую сторону от точки А).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1с.
Задача КЗ – на сложное движение точки. При ее решении движение точки по пластине считать относительным, а вращательное движение самой пластины – переносным и воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить расчеты, следует изобразить точку М на пластине в том положении, в котором нужно определить ее абсолютную скорость (или ускорение), а не в произвольном положении, показанном на рисунках к задаче. В случаях, относящихся к рис. К3.6 – К3.9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки М в момент времени t = 1 с и угол между радиусами СМ и СА в этот момент.
При решении задач на сложное движение точки рекомендуется такая последовательность.
1. Разложить движение на составляющие, определив абсолютное, относительное и переносное движения.
2. Выбрать две системы координат: подвижную и неподвижную.
3. Мысленно остановить переносное движение, определить скорость и ускорение точки в относительном движении.
4. Мысленно отвлекаясь от относительного движения, найти угловую скорость переносного движения, скорость и ускорение точки в переносном движении.
5. По известным угловой скорости переносного движения и скорости точки в относительном движении найти кориолисово ускорение точки.
6. Применив теорему сложения скоростей, определить искомую абсолютную скорость точки.
7. Пользуясь методом проекций, определить проекции абсолютного ускорения на оси координат.
8. По найденным проекциям абсолютного ускорения найти искомое абсолютное ускорение точки по величине и направлению.
Следует помнить, что Кориолисово ускорение может обращаться в нуль в следующих случаях.
1. Когда 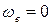 , т. е. когда переносное движение является поступательным или если угловая скорость переносного вращения в данный момент времени обращается в нуль.
, т. е. когда переносное движение является поступательным или если угловая скорость переносного вращения в данный момент времени обращается в нуль.
2. Когда 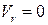 , т. е. когда относительная скорость в данный момент времени обращается в нуль.
, т. е. когда относительная скорость в данный момент времени обращается в нуль.
3. Когда  или
или  , т. е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или если в данный момент времени вектор
, т. е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или если в данный момент времени вектор  параллелен этой оси.
параллелен этой оси.