Пример 1: Дано:  ,
,  см,
см,  (см),
(см),  с.
с.
Определить: абсолютную скорость  и абсолютное ускорение
и абсолютное ускорение  точки М.
точки М.
Решение:
При решении задачи считаем движение точки по пластине относительным, а вращательное движение самой пластины – переносным. Выбираем подвижную  и неподвижную
и неподвижную  системы координат (рис. 14.4).
системы координат (рис. 14.4).
Определим положение точки на пластинке в момент времени  с:
с:
 см.
см.
Знак «минус» показывает, что точка М перемещается в сторону, противоположную положительному направлению отсчёта расстояния АМ вниз вдоль оси относительно точки А.
Точка М совершает сложное движение. Относительное движение – это движение точки М по пластинке вдоль оси  1, а переносным движением будет вращение системы координат
1, а переносным движением будет вращение системы координат  , неизменно связанной с пластиной, относительно неподвижной системы координат
, неизменно связанной с пластиной, относительно неподвижной системы координат  .
.
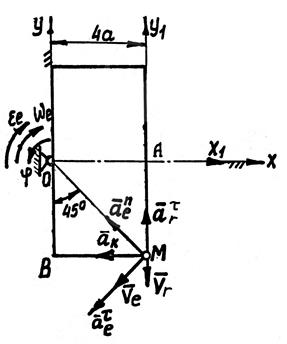
Рис. К3 1
Абсолютная скорость  .
.
Относительная скорость  ;
; 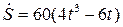 .
.
При  с
с  см/с, знак «минус» показывает, что вектор
см/с, знак «минус» показывает, что вектор  направлен вниз вдоль оси
направлен вниз вдоль оси 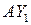 относительно точки А, в сторону отрицательных значений.
относительно точки А, в сторону отрицательных значений.
 ,
,  =120 см/с.
=120 см/с.
Переносная скорость
 ,
,
где  см, так как ОАМ – прямоугольный равнобедренный треугольник, так как
см, так как ОАМ – прямоугольный равнобедренный треугольник, так как  см;
см;  см, и
см, и  . Модуль угловой скорости
. Модуль угловой скорости  ,
, 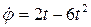 ,при
,при  с
с  с-1, знак «минус» показывает, что пластинка вращается в сторону, противоположную положительному направлению отсчёта угла
с-1, знак «минус» показывает, что пластинка вращается в сторону, противоположную положительному направлению отсчёта угла  (рис. 14.4), по часовой стрелке, а вектор
(рис. 14.4), по часовой стрелке, а вектор  перпендикулярен плоскости XOY чертежа и направлен вдоль оси, проходящей через точку О, за чертеж.
перпендикулярен плоскости XOY чертежа и направлен вдоль оси, проходящей через точку О, за чертеж.
 с-1,
с-1,  см/с.
см/с.
Вектор 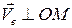 и направлен в сторону
и направлен в сторону  в сторону вращения пластины.
в сторону вращения пластины.
Угол между  и
и  равен 45°, тогда
равен 45°, тогда
 см/с.
см/с.
Абсолютное ускорение  , или
, или  .
.
Относительное касательное ускорение
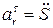 ;
;  .
.
При  с
с  см/с,
см/с,  см/с2 и направлено противоположно
см/с2 и направлено противоположно  так как
так как  = -120 см/с.
= -120 см/с.
Относительное движение точки М направлено по прямой АВ, поэтому

Переносное касательное ускорение  , где угловое ускорение
, где угловое ускорение  ,
,  . При
. При  с
с  с-2. Знаки
с-2. Знаки  и
и  совпадают, значит, вращение пластинки ускоренное, направления
совпадают, значит, вращение пластинки ускоренное, направления  и
и  совпадают.
совпадают.
 с-2,
с-2,  см/с2.
см/с2.
Переносное нормальное ускорение  см/с2 и направлено от М к О.
см/с2 и направлено от М к О.
Ускорение Кориолиса
 см/с2.
см/с2.
Вектор  направлен в соответствии с векторным равенством параллельно оси ОХ (рис. 14.4).
направлен в соответствии с векторным равенством параллельно оси ОХ (рис. 14.4).
Модуль абсолютного ускорения определим методом проекций:
 см/с2;
см/с2;
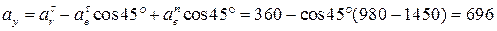 см/с2;
см/с2;
 см/с2.
см/с2.
Пример 2: Диск радиусом R = 20 см вращается вокруг оси, перпендикулярной плоскости диска и проходящей через точку О, согласно уравнению  . По ободу диска от точки А движется точка М согласно уравнению
. По ободу диска от точки А движется точка М согласно уравнению  см. Для момента времени t = 1 с определить величину абсолютной скорости и абсолютного ускорения точки М (рис. К3.2).
см. Для момента времени t = 1 с определить величину абсолютной скорости и абсолютного ускорения точки М (рис. К3.2).
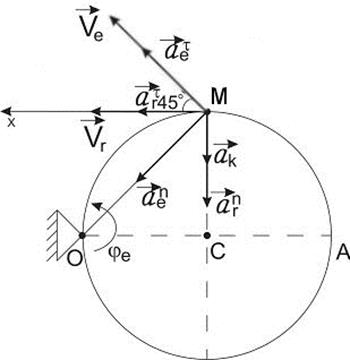
Рис. К3.2
Решение:
Убедимся, что точка М совершает сложное движение. Действительно, точка М движется по ободу диска и вместе с диском вращается вокруг оси О.
Движение точки М по ободу диска по заданному закону  будет относительным, вращение диска вокруг оси О -переносным.
будет относительным, вращение диска вокруг оси О -переносным.
Установим положение точки М на относительной траектории в данный момент времени, определив для этого значение центрального угла  .
.
 , т. е.
, т. е.  .
.
Положение точки М в данный момент времени указано на рисунке.
Абсолютная скорость точки М определяется геометрической суммой относительной и переносной скоростей
 .
.
Относительное движение точки является криволинейным. Поэтому вектор  относительной скорости направлен по касательной к ободу диска в точке М. Значение относительной скорости
относительной скорости направлен по касательной к ободу диска в точке М. Значение относительной скорости
 , при t = 1 с
, при t = 1 с  см/с.
см/с.
Переносное движение, т. е. движение диска, является вращательным. Поэтому вектор  переносной скорости, т. е. скорости той точки диска, с которой в данный момент совпала точка М, будет направлен перпендикулярно отрезку ОМ в сторону вращения диска. По модулю
переносной скорости, т. е. скорости той точки диска, с которой в данный момент совпала точка М, будет направлен перпендикулярно отрезку ОМ в сторону вращения диска. По модулю
 , где
, где  .
.
При t = 1 с  с-1. Значение
с-1. Значение  см.
см.
Тогда  см/с.
см/с.
Модуль абсолютной скорости определяем по формуле
 см/с.
см/с.
Для определения абсолютного ускорения точки М используем формулу абсолютного ускорения точки в развернутом виде
 .
.
Относительное нормальное ускорение равно:
 см/с2.
см/с2.
Вектор  направлен по радиусу диска к его центру С.
направлен по радиусу диска к его центру С.
Относительное касательное ускорение
 см/с2.
см/с2.
Вектор 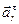 совпадает с направлением вектора относительной скорости. Переносное нормальное ускорение
совпадает с направлением вектора относительной скорости. Переносное нормальное ускорение
 см/с2.
см/с2.
Вектор  направлен вдоль ОМ к оси вращения О. Переносное касательное ускорение
направлен вдоль ОМ к оси вращения О. Переносное касательное ускорение  , где угловое ускорение
, где угловое ускорение  , при t = = 1 с
, при t = = 1 с  с-2.
с-2.
Тогда  см/с2.
см/с2.
Так как угловая скорость  и угловое ускорение
и угловое ускорение  одинаковы по знаку, то вектор
одинаковы по знаку, то вектор 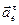 совпадает с направлением вектора
совпадает с направлением вектора  переносной скорости.
переносной скорости.
Ускорение Кориолиса определим по формуле
 .
.
Так как вектор  относительной скорости лежит в плоскости, перпендикулярной оси переносного вращения, то для определения направления кориолисова ускорения достаточно вектор
относительной скорости лежит в плоскости, перпендикулярной оси переносного вращения, то для определения направления кориолисова ускорения достаточно вектор  относительной скорости повернуть в сторону вращения на 90˚ в плоскости диска. По модулю кориолисово ускорение равно:
относительной скорости повернуть в сторону вращения на 90˚ в плоскости диска. По модулю кориолисово ускорение равно:
 , или
, или  см/с2.
см/с2.
Модуль абсолютного ускорения найдем методом проекций:
 см/с2,
см/с2,
 см/с2.
см/с2.
Окончательно модуль абсолютного ускорения равен:
 м/с2.
м/с2.
ДИНАМИКА
Задача Д1
Груз D массой т, получив в точке А начальную скорость 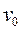 , движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости v груза (направлена против движения).
, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости v груза (направлена против движения).
В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила F, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная расстояние АВ =  или время t, движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. x = f(t), где х = BD. Трением груза о трубу пренебречь.
или время t, движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. x = f(t), где х = BD. Трением груза о трубу пренебречь.
Эта задача относится ко второй основной задаче динамики точки и заключается в том, что по заданным силам, приложенным к движущейся материальной точке, массе этой точки и начальным условиям ее движения, начальному положению и начальной скорости, требуется определить закон движения этой точки.



Задачи рекомендуется решать в следующем порядке.
1. Изобразить материальную точку в текущий момент времени.
2. Изобразить на рисунке активные силы и реакции связей, приложенные к материальной точке.
3. Выбрать систему координат. Начало координат системы следует помещать в начальном положении точки и оси координат направлять так, чтобы координаты точки в текущий момент и проекции скорости ее на эти оси были положительными.
4. Составить дифференциальные уравнения движения материальной точки. При этом следует помнить, что в полученных дифференциальных уравнениях проекции всех сил необходимо выразить через те переменные, от которых эти силы зависят.
5. Проинтегрировать полученные дифференциальные уравнения движения точки. Способ интегрирования уравнений зависит от их вида.
6. Составить начальные условия движения по тексту задачи.
7. Используя начальные условия движения, определить произвольные постоянные интегрирования.
8. Найденные произвольные постоянные подставить в результат интегрирования дифференциальных уравнений движения точки.
9. Воспользовавшись полученным уравнением движения материальной точки, определить искомые величины.
Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки на участке  , а затем на участке
, а затем на участке  . При решении задачи следует учесть изложенный выше план решения задач.
. При решении задачи следует учесть изложенный выше план решения задач.