В указанных нами предположениях о потоке требований и о длительности обслуживания задачи теории массового обслуживания приобретают некоторые черты, облегчающие проведение исследований. Мы отмечали уже вычислительную простоту. Теперь отметим более принципиальное соображение, которое станем развивать применительно к изучаемой задаче.
В каждый момент рассматриваемая система может находиться в одном из следующих состоянии: в момент t в системе находятся k требовании (k=0, 1, 2,...). Если k  rn, то в системе находятся и обслуживаются k требований, а m-k - приборов свободны. Если k
rn, то в системе находятся и обслуживаются k требований, а m-k - приборов свободны. Если k 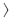 m, то m требований обслуживаются, а k-m находятся в очереди и ожидают обслуживания. Обозначим через
m, то m требований обслуживаются, а k-m находятся в очереди и ожидают обслуживания. Обозначим через  состояние, когда в системе находятся k требований. Таким образом, система может находиться в состояниях
состояние, когда в системе находятся k требований. Таким образом, система может находиться в состояниях  ... Обозначим через
... Обозначим через  — вероятность того, что система в момент t окажется в состоянии
— вероятность того, что система в момент t окажется в состоянии  .
.
Сформулируем, в чем заключается особенность изучаемых нами задач в сделанных предположениях. Пусть в некоторый момент 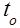 наша система находилась и состоянии
наша система находилась и состоянии 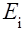 . Докажем, что последующее течение процесса обслуживания не зависит в смысле теории вероятностей от того, что происходило до момента
. Докажем, что последующее течение процесса обслуживания не зависит в смысле теории вероятностей от того, что происходило до момента 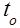 . Действительно, дальнейшее течение обслуживания полностью определяется тремя следующими факторами:
. Действительно, дальнейшее течение обслуживания полностью определяется тремя следующими факторами:
моментами окончания обслуживаний, производящихся в момент 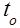 ;
;
моментами появления новых требований;
длительностью обслуживания требований, поступивших после 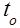 .
.
В силу особенностей показательного распределения длительность остающейся части обслуживания не зависит от того, как долго уже продолжалось обслуживание до момента  . Так как поток требований простейший, то прошлое не влияет на то, как много требований появится после момента
. Так как поток требований простейший, то прошлое не влияет на то, как много требований появится после момента  . Наконец длительность обслуживания требований, появившихся после
. Наконец длительность обслуживания требований, появившихся после  , никак не зависит от того, что и как обслуживалось до момента
, никак не зависит от того, что и как обслуживалось до момента  .
.
Известно, что случайные процессы, для которых будущее развитие зависит только от достигнутого в данный момент состояния и не зависит от того, как происходило развитие в прошлом, называются процессами Маркова или же процессами без последействия. Итак, система с ожиданием в случае простейшего потока и показательного времени обслуживания представляет собой случайный процесс Маркова. Это обстоятельство облегчает дальнейшие рассуждении.
3. Составление уравнений.
Задача теперь состоит в том, чтобы найти те уравнения, которым удовлетворяют вероятности 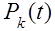 . Одно из уравнения очевидно, a именно для каждого t
. Одно из уравнения очевидно, a именно для каждого t
 (2)
(2)
Найдём сначала вероятность того, что и момент t .+h все приборы свободны. Это может произойти следующими способами:
· в момент t все приборы были свободны и за время h новых требований не поступало;
· в момент t один прибор был занят обслуживанием требования, все остальные приборы свободны; за время h обслуживание требования было завершено и новых требований не поступило.
Остальные возможности, как-то: были заняты два или три прибора и за время h работа на них біла закончена - имеют вероятность о(h), как легко в этом убедится.
Вероятность первого из указанных событий равна
 ,
,
вероятность второго события
 .
.
Таким образом
 .
.
Отсюда очевидным образом приходим уравнению
Перейдём теперь к составлению уравнений для 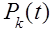 при
при  1. Рассмотрим отдельно два различных случая: 1
1. Рассмотрим отдельно два различных случая: 1  и
и 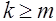 . Пусть в начале 1
. Пусть в начале 1 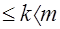 . Перечислим только существенные состояния, из которых можно прийти в состояние
. Перечислим только существенные состояния, из которых можно прийти в состояние  в момент t+h. Эти состояния таковы:
в момент t+h. Эти состояния таковы:
В момент t система находилась в состоянии  , за время h новых требований не поступило и ни один прибор не окончил обслуживания. Вероятность этого события равна:
, за время h новых требований не поступило и ни один прибор не окончил обслуживания. Вероятность этого события равна:
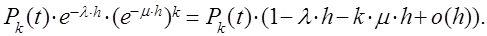
В момент t система находилась в состоянии  , за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна
, за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна
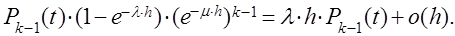
В момент t система находилась в состоянии  , за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна
, за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна
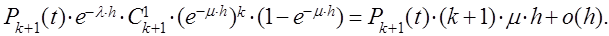 Все остальные мыслимые возможности перехода в состояние
Все остальные мыслимые возможности перехода в состояние  за промежуток времени h имеют вероятность, равную о(h).
за промежуток времени h имеют вероятность, равную о(h).
Собрав воедино найденные вероятности, получаем следующее равенство:
 Несложные преобразования приводят от этого равенства к такому уравнению для 1
Несложные преобразования приводят от этого равенства к такому уравнению для 1  ;
;
 (4)
(4)
Подобные же рассуждения для 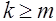 приводят к уравнению
приводят к уравнению
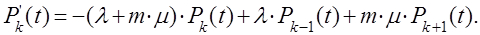 (5)
(5)
Для определения вероятностей 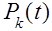 получили бесконечную систему дифференциальных уравнений (2)-(5). Её решение представляет несомненные технические трудности.
получили бесконечную систему дифференциальных уравнений (2)-(5). Её решение представляет несомненные технические трудности.
4. Определение стационарного решения.
В теории массового обслуживания обычно изучают лишь установившееся решение для 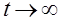 . Существование таких решений устанавливается так называемыми эргодическими теоремами, некоторые из них позднее будут установлены. В рассматриваемой задаче оказывается, что предельные или, как говорят обычно, стационарные вероятности существуют. Введём для них обозначения
. Существование таких решений устанавливается так называемыми эргодическими теоремами, некоторые из них позднее будут установлены. В рассматриваемой задаче оказывается, что предельные или, как говорят обычно, стационарные вероятности существуют. Введём для них обозначения 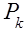 . Заметим дополнительно, что
. Заметим дополнительно, что 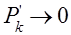 при
при 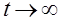 .
.
Сказанное позволяет заключить, что уравнения (3), (4), (5) для стационарных вероятностей принимают следующий вид:
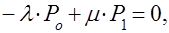 (6)
(6)
при 1 
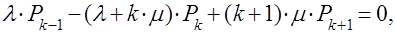 (7)
(7)
при 
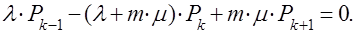 (8)
(8)
К этим уравнениям добавляется нормирующее условие
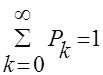 (9)
(9)
Для решения полученной бесконечной алгебраической системы введём обозначения: при 1 

при 
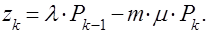
Система уравнений (6)-(8) в этих обозначениях принимает такой вид:

 при
при 
Отсюда заключаем, что при всех 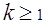
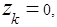
т.е. при 1 
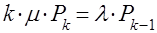 (10)
(10)
и при 
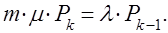 (11)
(11)
Введём для удобства записи обозначение
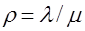 .
.
Уравнение (10) позволяет заключить, что при 1 
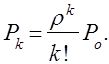 (12)
(12)
При  из (11) находим, что
из (11) находим, что

и, следовательно, при 
 (13)
(13)
Остаётся найти  . Для этого в (9) подставляем выражения
. Для этого в (9) подставляем выражения  из (12) и (13). В результате
из (12) и (13). В результате

так как бесконечная сумма, стоящая в квадратных скобках, сходится только при условии, что
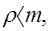 (14)
(14)
то при этом предположении находим равенство
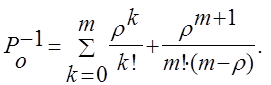 (15)
(15)
Если условие (14) не выполнено, т.е. если 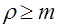 , то ряд, стоящий в квадратной скобке уравнения для определения
, то ряд, стоящий в квадратной скобке уравнения для определения  , расходится и, значит,
, расходится и, значит,  должно быть равно 0. Но при этом, как следует из (12) и (13), при всех
должно быть равно 0. Но при этом, как следует из (12) и (13), при всех  оказывается
оказывается 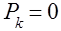 .
.
Методы теории цепей Маркова позволяют заключить, что при 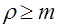 с течением времени очередь стремится к
с течением времени очередь стремится к 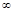 по вероятности.
по вероятности.
Поясним полученный результат на нескольких практических примерах, которые покажут, что обычные в практической деятельности подсчеты, основанные на чисто арифметических соображениях, при которых не учитывается специфика случайных колебаний в поступлении требований на обслуживание, приводят к серьезным просчетам.
Пусть врач успевает удовлетворительно осмотреть больного и заполнить его историю болезни в среднем за 15 минут. Планирующие органы из этого обычно делают вывод: за четырёхчасовый рабочий день врач должен принимать 16 человек. Однако больные приходят в случайные моменты времени. В результате при таком подсчете пропускной способности врача к нему неизбежно скапливается очередь, так как при проведенном подсчете  принимается равным 1. Те же заключения относятся и к расчету числа коек в больницах, числа работающих касс в магазинах, числа официантов в ресторанах и т. д. К сожалению, некоторые экономисты совершают такую же ошибку и при расчете погрузочных средств в карьерах, числе приемщиков на элеваторах, числе причалов в морских портах и пр.
принимается равным 1. Те же заключения относятся и к расчету числа коек в больницах, числа работающих касс в магазинах, числа официантов в ресторанах и т. д. К сожалению, некоторые экономисты совершают такую же ошибку и при расчете погрузочных средств в карьерах, числе приемщиков на элеваторах, числе причалов в морских портах и пр.
Во всем дальнейшем мы предполагаем, что условие (14) выполнено.
5. Некоторые подготовительные результаты.
Для задачи с ожиданием основной характеристикой качества обслуживания является длительность ожидания требованием начала обслуживания. Длительность ожидания представляет собой случайную величину, которую обозначим буквой  . Рассмотрим сейчас только задачу определения распределения вероятностей длительности ожидания в уже установившемся процессе обслуживания. Обозначим далее через
. Рассмотрим сейчас только задачу определения распределения вероятностей длительности ожидания в уже установившемся процессе обслуживания. Обозначим далее через 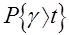 вероятность того, что длительность ожидания превзойдёт t, и через
вероятность того, что длительность ожидания превзойдёт t, и через 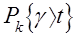 вероятность неравенства, указанного в скобке при условии, что в момент поступления требования, для которого подсчитывается длительность ожидания, в очереди уже находится k требований. В силу формулы полной вероятности имеем равенство
вероятность неравенства, указанного в скобке при условии, что в момент поступления требования, для которого подсчитывается длительность ожидания, в очереди уже находится k требований. В силу формулы полной вероятности имеем равенство
 (16)
(16)
Прежде чем преобразовать эту формулу к виду, удобному для использования, приготовим некоторые необходимые для дальнейшего сведения. Прежде всего для случаев m=1 и m=2 найдем простые формулы для  . Несложные преобразования приводят к таким равенствам: при m= 1
. Несложные преобразования приводят к таким равенствам: при m= 1
 =1-
=1-  , (17)
, (17)
а при m=2
 (18)
(18)
Вычислим теперь вероятность того, что все приборы будут заняты в какой-то наудачу взятый момент. Очевидно, что эта вероятность равна
 (19)
(19)
Эта формула для m=1 принимает особенно простой вид:
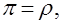 (20)
(20)
при m=2
 (21)
(21)
В формуле (19)  может принимать любое значение от 0 до m (исключительно). Так что в формуле (20)
может принимать любое значение от 0 до m (исключительно). Так что в формуле (20)  < 1, а в (21)
< 1, а в (21)  <2.
<2.
6. Определение функции распределения длительности ожидания.
Если в момент поступления требования в очереди уже находились k-m требований, то, поскольку обслуживание происходит в порядке очередности, вновь поступившее требование должно ожидать, когда будут обслужены k-m+ 1 требований. Пусть 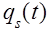 означает вероятность того, что за промежуток времени длительности t после поступления интересующего требования закончилось обслуживание ровно s требований. Ясно, что при
означает вероятность того, что за промежуток времени длительности t после поступления интересующего требования закончилось обслуживание ровно s требований. Ясно, что при  имеет место равенство
имеет место равенство

Так как распределение длительности обслуживания предположено показательным и не зависящим ни от того, сколько требований находится в очереди, ни от того, как велики длительности обслуживания других требований, то вероятность за время t не завершить ни одного обслуживания (т.е. вероятность того, что не освободится ни один из приборов) равна
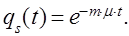
Если все приборы заняты обслуживанием и ещё имеется достаточная очередь требований, которые ожидают обслуживания, то поток обслуженных требований будет простейшим. Действительно, в этом случае все три условия — стационарность, отсутствие последействия и ординарность — выполнены. Вероятность освобождения за промежуток времени t ровно s приборов равна (это можно показать и простым подсчетом)
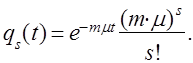
Итак,
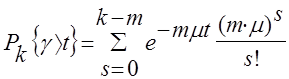
и, следовательно,

Но вероятности 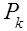 известны:
известны:
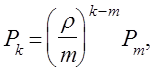
поэтому

Очевидными преобразованиями приводим правую часть последнего равенства к виду

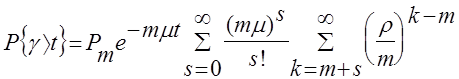 =
=

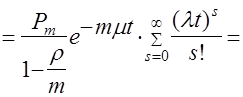
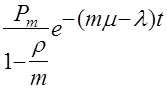 .
.
Из формул (18) и (19) следует, что  поэтому при m
поэтому при m  0
0
 (22)
(22)
Само собой разумеется, что при t  0
0
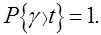
Функция 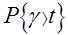 имеет в точке t=1 разрыв непрерывности, равный вероятности застать все приборы занятыми.
имеет в точке t=1 разрыв непрерывности, равный вероятности застать все приборы занятыми.
7. Средняя длительность ожидания.
Формула (22) позволяет находить все интересующие числовые характеристики длительности ожидания. В частности, математическое ожидание длительности ожидания начала обслуживания или, как предпочитают говорить, средняя длительность ожидания равна
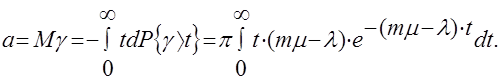
Несложные вычисления приводят к формуле
 (23)
(23)
Дисперсия величины  равна
равна

Формула (23) даёт среднюю длительность ожидания одного требования. Найдем среднюю потерю времени требованиями, пришедшими в систему обслуживания в течение промежутка времени T. За время T в систему поступает  требований и среднем; общая потеря ими времени па ожидание в среднем равна
требований и среднем; общая потеря ими времени па ожидание в среднем равна
 (24)
(24)
Приведем небольшие арифметические подсчеты, которые продемонстрируют нам, как быстро возрастают суммарные потери времени па ожидание с изменением величины 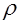 . При этом мы ограничиваемся случаем Т=1 и рассматриваем лишь самые малые значения т: т =1 и т=2.
. При этом мы ограничиваемся случаем Т=1 и рассматриваем лишь самые малые значения т: т =1 и т=2.
При т =1 в силу (20)

При р=0,1; 0,3; 0,5; 0,9 значение а 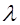 приблизительно равно 0,011; 0,267; 0,500; 1,633; 8,100.
приблизительно равно 0,011; 0,267; 0,500; 1,633; 8,100.
При m=2 в силу (24)


При 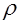 =0,1; 1,0; 1,5; 1,9 значение а
=0,1; 1,0; 1,5; 1,9 значение а 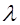 приблизительно равно 00003; 0,333; 1,350; 17,537.
приблизительно равно 00003; 0,333; 1,350; 17,537.
Приведённые данные иллюстрируют хорошо известный факт относительно большой чувствительности систем обслуживания, уже достаточно сильно загруженных, к возрастанию загрузки. Потребитель при этом сразу ощущает значительное возрастание длительности ожидания. Этот факт обязательно следует учитывать при расчёте загрузки оборудования в системах массового обслуживания.