Основные величины, характеризующие движение жидкости или газа. Линейная и объёмная скорости; соотношение между ними.
Основной характеристикой любого движения является его скорость. В случае течения жидкости (или газа) термин „скорость“ применяется в двух смыслах. Скорость перемещения самих частиц жидкости (или плывущих вместе с жидкостью мелких тел – например, эритроцитов в крови) обозначают υ и называют линейной скоростью. 
м/с 
, где х – координата частицы (при равномерном движении можно написать 
). Однако, на практике чаще важнее знать объём V жидкости, протекающей в данном потоке (в трубе, в русле реки, в кровеносном сосуде и т.п.) за единицу времени. Эту величину называют объёмной скоростью и обозначают Q.
Q =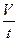 
. 
(1)
Между линейной скоростью υ и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S (см. рисунок 1).
1 2
S 1 V
X
Рис. 1
Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1. Через некоторое время t он переместится в положение 2, отстоящее на расстояние x = υ·t. При этом через трубку пройдёт объём жидкости V = S·x. Объёмная скорость жидкости Q при этом будет равна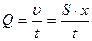 
. Но 
, поэтому
Q = S ·υ (2)
Если течение стационарно, то
Q = S1·u1 = S2·u2 = S3·u3 = ……. = const (3)
Это уравнение неразрывности струи.
Течение идеальной жидкости. Теорема Бернулли.
Идеальная жидкость – жидкость несжимаемая и неимеющая силы внутреннего трения. Следовательно при движении жидкости не происходит диссипации энергии, ее полная энергия постоянна. Если жидкость движется под действием внешнего давления, то ее полная энергия есть сумма кинетической энергии, потенциальной энергии,силы тяжести и потенциальной энергии давления. 
. Для идеальной жидкости Е= const. 
. Разделим на объем жидкости V, так как жидкость несжимаема, V = const.
|
|
, 
- плотность жидкости.
уравнение (теорема) Бернулли.
р – внешнее статическое давление, которое, согласно закона Паскаля, передается жидкостью во все стороны без изменения. 
давление силы тяжести жидкости или гидростатическое давление.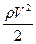 
- давление, создаваемое вследствие движения жидкости -–динамическое давление, направленное по вектору скорости жидкости. Для горизонтального течения жидкости, когда 
=const, можно уравнение Бернулли упростить: 
.
При нормальном кровообращении, как нетрудно подсчитать, динамическое давление составляет всего 1% 3% от полного. Например, в аорте линейная скорость крови около 0,7 метра в секунду, откуда 
(плотность крови ≈ 1000 кг.м –3 ). Полное давление крови в аорте (среднее) около 120 мм.рт.столба. Учитывая, что 1 мм.рт.ст. = 133 паскаля, получаем, что полное давление равно 16.10 3 Па, то есть рдинамич ≈ 1,5%. Однако, при усиленной физической нагрузке, а также при некоторых заболеваниях динамическое давление заметно возрастает, и его необходимо учитывать.
Вязкость жидкости. Закон Ньютона. Ньютоновские и неньютоновские жидкости.
В реальных жидкостях всегда существуют силы трения. Причины трения – межмолекулярные взимодействия. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трением или вязкостью (эти термины являются синонимами).
|
|
Рассмотрим два слоя жидкости, движущиеся с разными скоростями (рис. 5). Расстояние между слоями равно х.
S
SSs v 1
Х S v 2
 |
Рис. 5
Выделим в каждом слое площадку с площадью S. Ньютон показал, что сила трения между этими слоями равна:
(6)
(знак „минус“ показывает, что сила трения направлена навстречу движению). Эта формула носит название формула Ньютона.
Коэффициент η (эта) называется коэффициент вязкости или просто вязкость (реже говорят „коэффициент внутреннеготрения“). F = - η grad 
S Размерность величины η есть Па.с;
Ньютоновские и неньютоновские жидкости
Для большинства жидкостей коэффициент вязкости η при постоянной температуре есть постоянная величина, зависящая только от природы жидкости и не зависящая от её скорости (точнее, от градиента скорости; см. формулу «8»). Такие жидкости принято называть „ньютоновскими“, то есть строго подчиняющимися закону Ньютона.
Однако, опыт показал, что для ряда жидкостей η ≠ const. При малых градиентах скорости (что чаще всего бывает, когда сама скорость движения жидкости мала) вязкость относительно велика, но с ростом градиента скорости вязкость уменьшается, приближаясь к некоторому, сравнительно малому постоянному значению η0.
Такие жидкости называются „ неньютоновскими“ К ним относятся, во-первых, растворы веществ, молекулы которых в растворе образуют достаточно сильные межмолекулярные связи. Эти связи затрудняют перескоки молекул из одного положения в другое и тем самым снижают текучесть раствора, то есть увеличивают его вязкость. Плазма крови содержит большое количество растворённых белков, и в ней плавает большое число клеток (в основном – эритроцитов); кровь – это типичная неньютоновская жидкость. Поэтому, в частности, в капиллярах, где скорость течения крови мала, вязкость крови заметно больше, чем в крупных сосудах; это необходимо учитывать при расчётах движения крови в системе кровообращения.
|
|