Практическая работа №9.
Тема: «Решение дифференциальных уравнений»
Цель работы:
развитие навыков решения простейших дифференциальных уравнений, нахождение общих и частных решений.
Теоретическая часть
Понятие дифференциального уравнения
1. Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную 
;
2) зависимую переменную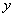 
(функцию);
3) первую производную функции: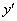 
.
Решить дифференциальное уравнение – это значит, найти множество функций 
, которые удовлетворяют данному уравнению.
Общим решением дифференциального уравнения 1-го порядка называется такое его решение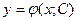 
, которое является функцией переменной х и произвольной независимой постоянной С.
Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых начальных условиях.
Рассмотрим уравнение первого порядка, разрешенное относительно первой производной:
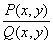
где неизвестной является функция у=у(х), а известной является функция f(x, y).
Учитывая, что и полагая возможным представить f (x, y) в виде
,уравнение можно записать в так называемой дифференциальной форме:
Если в данном уравнении P(x, y) и Q(x, y) можно представить в виде P(x, y)=N(x)R(y) и Q(x, y)=M(x)K(y), то уравнение в дифференциальной форме запишется как
N(x)R(y)dx+M(x)K(y)dy=0. (1)
Это уравнение называется уравнением с разделяющимися переменными.
Метод его решения: разделив (1) на произведение M(x)R(y) получим
(2)
Интегрируя (2), получим общий интеграл исходного уравнения:
(3)
Определение: Задача нахождения решения уравнения, удовлетворяющего условию (4)
где числа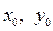 
– заданные числа, называется задачей Коши. Условие (4) называется начальным условием. Решение уравнения, удовлетворяющее начальному условию (4), называется решением задачи Коши и записывается в виде
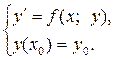. (5)
Решить задачу Коши (5) означает найти интегральную кривую дифференциального уравнения, которая проходит через заданную точку 
.
Пример1. Решить дифференциальное уравнение 
где 
.
В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
Следующий этап – интегрирование дифференциального уравнения. Интегрируем обе части:
Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть, – это общий интеграл.
Вместо записи обычно пишут 
.
В данном случае:
Функция представлена в явном виде. Это и есть общее решение.
Множество функций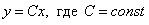 
является общим решением дифференциального уравнения .
Придавая константе 
различные значения, можно получить бесконечно много частных решений дифференциального уравнения.
Пример 2. Найти частное решение дифференциального уравнения 
, удовлетворяющее начальному условию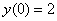 
По условию требуется найти частное решение ДУ, удовлетворяющее начальному условию. Такая постановка вопроса также называется задачей Коши.
Сначала находим общее решение.
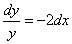
Интегрируем уравнение:
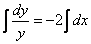
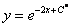
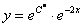
Итак, общее решение: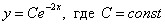 
. На завершающем этапе нужно найти частное решение, удовлетворяющее заданному начальному условию .
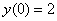Необходимо подобрать такое значение константы , чтобы выполнялось заданное начальное условие .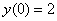
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:
В общее решение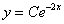 
подставляем найденное значение константы 
:
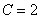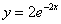– это и есть нужное нам частное решение.
Пример 3. Решить дифференциальное уравнение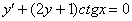 
Решение: Переписываем производную в нужном нам виде:
Переносим второе слагаемое в правую часть со сменой знака:
Переменные разделены, интегрируем обе части:
= > 
= > 
= >
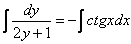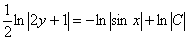
Решение распишу очень подробно:
= > 
= > 
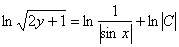Ответ: общий интеграл: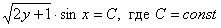 
Пример 4. Найти частное решение дифференциального уравнения 
, удовлетворяющее начальному условию 
. Выполнить проверку.
Решение: Сначала найдем общее решение.Данное уравнение уже содержит готовые дифференциалы 
и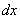 
, а значит, решение упрощается. Разделяем переменные:
Интегрируем уравнение:
= > 
= > 
= >
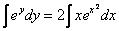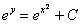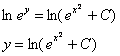
общее решение:
Найдем частное решение, соответствующее заданному начальному условию
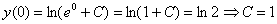
Подставляем найденное значение константы 
в общее решение.
Ответ: частное решение: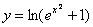 
| ХОД РАБОТЫ Внимательно изучите теоретическую часть практической работы, основные и дополнительные источники и дайте развёрнутые ответы на контрольные вопросы: 1. Сформулируйте определение дифференциального уравнения 2. Сформулируйте понятие общего решения дифференциального уравнения 3. Сформулируйте понятие частного решения дифференциального уравнения 4. Дайте определение дифференциального уравнения первого порядка с разделяющимися переменными 5. Дайте определение задачи Коши. 6. Приведите примеры решения дифференциальных уравнений |
Основные источники:
1. Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 10-е изд., стер. – М.: Издательский центр «Академия», 2018.
Дополнительные источники:
2. Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2015.
3. Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 11-е изд., перераб. И доп. –М.: издательство Юрайт, 2015.
4. Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: https://school-collection.edu.ru/catalog/– Загл. с экрана;
5. Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: https://window.edu.ru/– Загл. с экрана