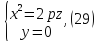Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов →a, →b, →ca→, b→, c→ в трехмерном пространстве.
Отложим для начала векторы →a, →b, →ca→, b→, c→ от одной точки. Ориентация тройки →a, →b, →ca→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора →cc→. От того, в какую сторону осуществляется кратчайший поворот от вектора →aa→ к →bb→ с конца вектора →cc→, будет определен вид тройки→a, →b, →ca→, b→, c→.
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов →a, →b, →ca→, b→, c→ называется правой, если по часовой стрелке – левой.
Векторным произведением двух векторов →aa→ и →bb→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы →aa→ и →bb→ коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору →aa→ и вектору →bb→ т.е. ∠(→a→c)=∠(→b→c)=π2∠a→c→=∠b→c→=π2;
- его длина определяется по формуле: ∣∣→c∣∣=∣∣→a∣∣⋅∣∣∣→b∣∣∣⋅sin∠(→a,→b)c→=a→·b→·sin∠a→,b→;
- тройка векторов →a, →b, →ca→, b→, c→ имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов →aa→ и →bb→ имеет следущее обозначение: [→a×→b]a→×b→.
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
Определение 2
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов →a=(ax; ay; az)a→=(ax; ay; az) и →b=(bx; by; bz)b→=(bx; by; bz) называют вектор→c=[→a×→b]=(ay⋅bz−az⋅by)⋅→i+(az⋅bx−ax⋅bz)⋅→j+(ax⋅by−ay⋅bx)⋅→kc→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где →i, →j, →ki→, j→, k→ являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты →i, →j, →ki→, j→, k→, вторая строка содержит координаты вектора →aa→, а третья – координаты вектора →bb→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так:
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой∣∣→c∣∣=∣∣→a∣∣⋅∣∣∣→b∣∣∣⋅sin∠(→a,→b)c→=a→·b→·sin∠a→,b→.
Сме́шанное произведе́ние {\displaystyle (\mathbf {a},\mathbf {b},\mathbf {c})} векторов {\displaystyle \mathbf {a},\mathbf {b},\mathbf {c} } — скалярное произведение вектора {\displaystyle \mathbf {a} } на векторное произведение векторов {\displaystyle \mathbf {b} } и {\displaystyle \mathbf {c} }:
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический смысл: модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами {\displaystyle \mathbf {a},\mathbf {b},\mathbf {c} }.
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так:
Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу
В системе координат заданы точки A(0, 1, 0), B(3, −1, 5), C(1, 0, 3), D(−2, 3, 1)A(0, 1, 0), B(3, -1, 5), C(1, 0, 3), D(-2, 3, 1). Следует определить объем тетраэдра, который расположен на этих точках.
.
ассмотрим задачу приведения уравнения линии второго порядка к наиболее простому (каноническому) виду.
Напомним, что алгебраической линией второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат может быть задано уравнением вида где — многочлен второй степени двух переменных. Требуется найти прямоугольную систему координат, в которой уравнение линии приняло бы наиболее простой вид.
Результатом решения поставленной задачи является следующая основная теорема (3.3)
Классификация алгебраических линий второго порядка (теорема 3.3)
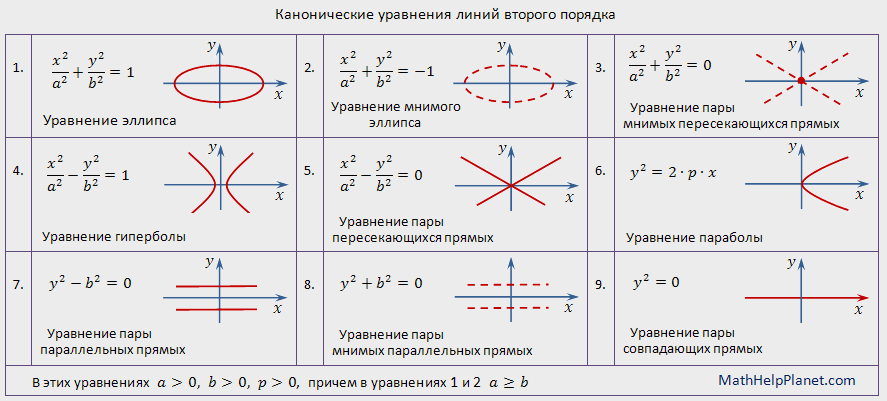
Для любой алгебраической линии второго порядка существует прямоугольная система координат, в которой уравнение этой линии принимает один из следующих девяти канонических видов:
Теорема 3.3 дает аналитические определения линий второго порядка. Согласно пункту 2 замечаний 3.1, линии (1), (4), (5), (6), (7), (9) называются вещественными (действительными), а линии (2), (3), (8) — мнимыми.
Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:
Гиперболо́ид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность). В математике гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1} (однополостный гиперболоид),
где a и b — действительные полуоси, а c — мнимая полуось;
ли
{\displaystyle -{x^{2} \over a^{2}}-{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1} (двуполостный гиперболоид),
где a и b — мнимые полуоси, а c — действительная полуось.
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:
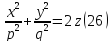
где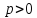 
и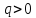 
.
Уравнение (26) называется каноническим уравнением эллиптического параболоида.
Гиперболический параболоид.
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением:
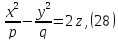
где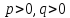 
.
Уравнение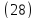 
называется каноническим уравнением гиперболического параболоида.
Рассмотрим сечение параболоида плоскостью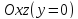 
. Получаем уравнение:
