Это старый и в настоящее время забытый способ решения квадратных уравнений.
Номограмма даёт значения положительных корней уравнения z2 + pz + q = 0. Если уравнение имеет корни разных знаков, то, найдя по номограмме положительный корень, отрицательный находят, вычитая положительный из – р.
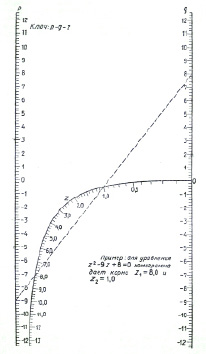
Рис. 6. Вид монограммы для решения уравнения z2 + pz + q = 0
В случае, когда оба корня отрицательны, берут z = – t и находят по номограмме два положительных корня t1; t2 уравнения t2 + – pt + z = 0, а затем z1 = – t1; z2 = – t2.
Если коэффициенты p и q выходят за пределы шкал, выполняют подстановку z = kt и решают посредством номограммы уравнение
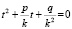 ,
,
где k берётся с таким расчётом, чтобы имели место неравенства
 ;
;  .
.
Вид монограммы для решения уравнения z2 + pz + q = 0 можно найти на рис. 6.
«Плюсы» и «минусы» различных способов решения
| Название способа решения квадратных уравнений | Плюсы | Минусы |
| Решение квадратных уравнений по формуле | Можно применить ко всем квадратным уравнениям. | Нужно выучить формулы. |
| Разложение левой части уравнения на множители | Дает возможность сразу увидеть корни уравнения. | Нужно правильно вычислить слагаемых для группировки. |
| Метод выделения полного квадрата | За минимальное количество действий можно найти корни уравнений | Нужно правильно найти все слагаемые для выделения полного квадрата. |
| Решение уравнений с использованием теоремы Виета | Достаточно легкий способ, дает возможность сразу увидеть корни уравнения. | легко находятся только целые корни. |
| Свойства коэффициентов квадратного уравнения | Не требует особых усилий | Подходит только к некоторым уравнениям |
| Решение уравнений способом переброски | За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета. | легко найти только целые корни. |
| Геометрический способ решения квадратных уравнений | Наглядный способ. | похож на способ выделения полного квадрата |
| Графическое решение квадратного уравнения | Наглядный способ | Могут быть не точности при составлении графиков |
| Решение квадратных уравнений с помощью циркуля и линейки | Наглядный способ | Могут быть не точности |
| Решение квадратных уравнений с помощью номограммы | Наглядный способ, прост в применении. | Не всегда под рукой имеется номограмма. |
График квадратичной функции.
Квадратичная функция
•Квадратичной функцией называется функция вида y=ax2+bx+c, где a,b,c - числа, причем a≠0.
•Графиком квадратичной функции является парабола.
Чтобы построить график функции y=x2 составим таблицу значений
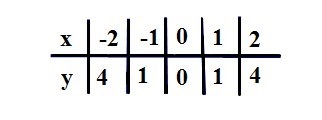
и построим график, используя полученные точки:
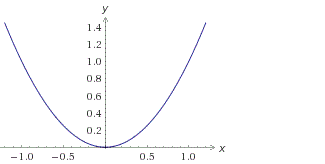
Внимание! Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции y=x2 при любых значениях остальных коэффициентов.
График функции y=-x2 имеет вид:

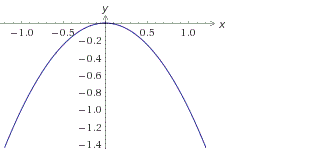
Итак:
•Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
•Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй этап построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) - это точки пересечения графика функции y=f(x) с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции y=f(x) с осью ОХ, нужно решить уравнение f(x)=0.
В случае квадратичной функции y=ax2+bx+c нужно решить квадратное уравнение ax2+bx+c=0.
В процессе решения квадратного уравнения мы находим дискриминант: D=b2-4ac, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если D<0,то уравнение ax2+bx+c=0 не имеет решений, и, следовательно, парабола y=ax2+bx+c не имеет точек пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:
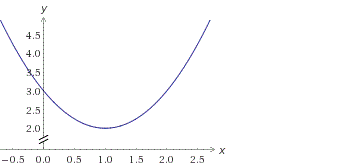
2. Если D=0,то уравнение ax2+bx+c=0 имеет одно решение, и, следовательно, парабола y=ax2+bx+c имеет одну точку пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:

3. Если D>0, то уравнение ax2+bx+c=0 имеет два решения, и, следовательно, парабола y=ax2+bx+c имеет две точки пересечения с осью ОХ: 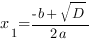 ,
, 
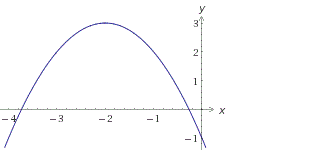
Если a>0, то график функции выглядит примерно так:

Значит, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный этап построения графика квадратичной функции – координаты вершины параболы:
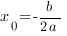

Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один этап построения графика функции – точка пересечения параболы y=ax2+bx+c с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы y=ax2+bx+c с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c.