конечно-разностная схема устойчива, если для малых возмущений входных данных (начально-краевых условий и правых частей) конечно-разносная схема обеспечивает малые возмущения сеточной функции uh т.е. решение с помощью конечно-разностной схемы находится под контролем входных данных.
Если во входные данные fn входят только начальные условия или только краевые условия, или только правые части, то говорят об устойчивости соответственно по начальным условиям, по краевым условиям или по правым частям.
Из математической физики известно, что решение начально-краевых задач представляется в виде следующего ряда:
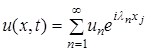, (16)
где λn – собственные значения
– собственные значения функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т.е. решение может быть представлено в виде суперпозиции отдельных гармоник 
, каждая из которых есть произведение функции времени и функции пространственной переменной, причем последняя по модулю ограничена сверху единицей при любых значениях переменной x.
В то же время функция времени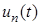 
, называемая амплитудной частью гармоники, никак не ограничена, и, по всей вероятности, именно амплитудная часть гармоник является источником неконтролируемого входными данными роста функции и, следовательно, источником неустойчивости.
Таким образом, если конечно-разностная схема устойчива, то отношение амплитудной части гармоники на верхнем временном слое к амплитудной части на нижнем временном слое по модулю должно быть меньше единицы.
Если разложить значение сеточной функции 
в ряд Фурье по собственным функциям:
(17)
где амплитудная часть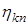 
может быть представлена в виде произведения
(18)
где 
– размерный и постоянный сомножитель амплитудной части,
k – показатель степени (соответствующий номеру временного слоя) сомножителя, зависящего от времени.
Тогда подставив (17) в конечно-разностную схему, можно по модулю оценить отношение амплитудных частей на соседних временных слоях.
Однако поскольку операция суммирования линейна и собственные функции ортогональны для различных индексов суммирования, то в конечно-разностную схему вместо сеточных значений достаточно подставить одну гармонику разложения (17) (при этом у амплитудной части убрать индекс n), т.е.
(19)
Таким образом, если конечно-разностная схема устойчива по начальным данным, то
, (20)
т. е. условие (20) является необходимым условием устойчивости.
Схема Кранка-Николсона
параболическое дифференциальное уравнение конечная разность
Явная конечно разностная схема, записанная в форме
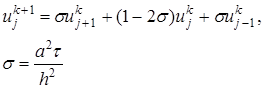(21)
обладает тем достоинством, что решение на верхнем временном слое tk+l получается сразу (без решения СЛАУ) по значениям сеточной функции на нижнем временном слое tk, где решение известно (при k = 0 значения сеточной функции формируются из начального условия). Но эта же схема обладает существенным недостатком, поскольку она является условно устойчивой. С другой стороны, неявная конечно-разностная схема, записанная форме
(22)
приводит к необходимости решать СЛАУ, но зато эта схема абсолютно устойчива.
Проанализируем схемы (21) и (22). Пусть точное решение, которое неизвестно, возрастает по времени, т.е.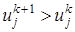 
. Тогда, в соответствии с явной схемой (21), разностное решение будет заниженным по сравнению с точным, так как 
определяется по меньшим значениям сеточной функции на предыдущем временном слое, поскольку решение является возрастающим по времени.
Для неявной схемы (22) на возрастающем решении, наоборот, решение завышено по сравнению с точным, поскольку оно определяется по значениям сеточной функции на верхнем временном слое.
На убывающем решении картина изменяется противоположным образом: явная конечно-разностная схема завышает решения, а неявная — занижает (Рисунок 4).
На основе этого анализа возникла идея о построении более точной неявно-явной конечно-разностной схемы с весами при пространственных конечно-разностных операторах, причем при измельчении шагов тик точное (неизвестное) решение может быть взято в «вилку» сколь угодно узкую, так как если явная и неявная схемы аппроксимируют дифференциальную задачу и эти схемы устойчивы, то при стремлении сеточных характеристик τ и h к нулю решения по явной и неявной схемам стремятся к точному решению с разных сторон.
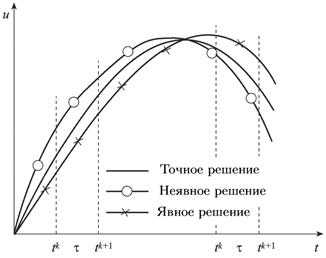
Рисунок 4 – Двусторонний метод аппроксимации
Проведенный анализ дал блестящий пример так называемых двусторонних методов, исследованных В. К. Саульевым
Рассмотрим неявно-явную схему с весами для простейшего уравнения теплопроводности:
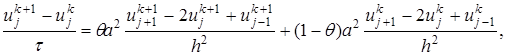(23)
где θ – вес неявной части конечно-разностной схемы,
θ -1 – вес для явной части
Причем 
. При θ=1 имеем полностью неявную схему, при θ=0 – полностью явную схему, а при θ=1/2 – схему Кранка-Николсона.
В соответствии с гармоническим анализом для схемы (23) получаем неравенство
,
откуда
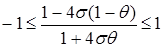(24)
причем правое неравенство выполнено всегда.
Левое неравенство имеет место для любых значений σ, если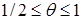 
. Если же вес θ лежит в пределах 
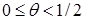, то между σ и θ из левого неравенства устанавливается связь
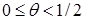(25)
являющаяся условием устойчивости неявно-явной схемы с весами (23), когда вес находится в пределах .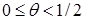
Таким образом, неявно-явная схема с весами абсолютно устойчива при 
и условно устойчива с условием (25) при .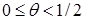
Рассмотрим порядок аппроксимации неявно-явной схемы с весами, для чего разложим в ряд Тейлора в окрестности узла (xj,tk) на точном решении значения сеточных функций 
по переменной t, 
, 
по переменной х и полученные разложения подставим в (23):
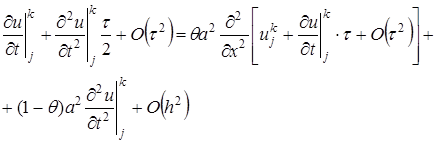
В этом выражении дифференциальный оператор 
от квадратной скобки в соответствии с дифференциальным уравнением равен дифференциальному оператору 
, в соответствии с чем вышеприведенное равенство приобретает вид
После упрощения получаем
,
откуда видно, что для схемы Кранка-Николсона (θ = 1/2) порядок аппроксимации схемы (23) составляет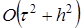 
, т.е. на один порядок по времени выше, чем для обычных явных или неявных схем. Таким образом, схема Кранка-Николсона при θ = 1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной х.
Используем в уравнение (23) подстановку r=a2k/h2. Но в то же время его нужно решить для трех "еще не вычисленных" значени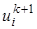й 
, 
, и 
. Это возможно, если все значения перенести в левую часть уравнения. Затем упорядочим члены уравнения (23) и в результате получим неявную разностную формулу
(26)
для i=2,3,…,n-1. Члены в правой части формулы (26) известны. Таким образом, формула (26) имеет вид линейной трехдиагональной системы АХ=В. Шесть точек, используемых в формуле Кранка-Николсона (26), вместе с промежуточной точкой решетки, на которой основаны численные приближения, показаны на рисунке 5.
Рисунок 5 – Шаблон (схема) метода Кранка-Николсона
Иногда в формуле (26) используется значение r=1. В этом случае приращение по оси t равно 
, формула (26) упрощается и принимает вид
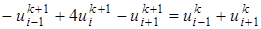, (27)
для i=2,3,…,n-1. Граничные условия используются в первом и последнем уравнениях (т. е. в 
и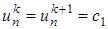 
соответственно).
Уравнения (27) особенно привлекательны при записи в форме трехдиагональной матрицы АХ = В.
Если метод Кранка-Николсона реализуется на компьютере, то линейную систему АХ = В можно решить либо прямым методом, либо итерационным.
2. Практическая часть
Постановка задачи
Используем метод Кранка-Николсона, чтобы решить уравнение
,
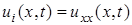где xϵ(0;1),
tϵ(0;0.1),
с начальным условием
,
где t=0,
xϵ(0;1),
и граничными условиями
u(0,t) = g1(t) ≡ 0,
u(1,t) = g2(t) ≡ 0.
Решение в ППП MatLab
Решение будем искать в ППП MatLab 7. Создадим четыре выполняемых m-фала: crnich.m – файл-функция с реализацией метода Кранка-Николсона; trisys.m – файл-функция метода прогонки; f.m – файл-функция задающая начальное условие задачи; fе.m – файл-функция задающая функцию определяющую точное решение задачи(найдена аналитическим путем). Листинги программ представлены в приложении А.
Для простоты возьмем шаг Δх = h = 0,1 и Δt = к = 0,01. Таким образом, соотношение r =1. Пусть решетка имеет n=11 столбцов в ширину и m=11 рядов в высоту.
Анализ результатов
Решения для данных параметров отразим в таблице 1. Трехмерное изображение данных из таблицы покажем на рисунке 5.
Таблица 1 – Значения u(хi, ti), полученные методом Кранка-Николсона
| xi | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| ti | |||||||||||
| 1.1180 | 1.5388 | 1.1180 | 0.3633 | 0.3633 | 1.1180 | 1.5388 | 1.1180 | ||||
| 0.01 | 0.6169 | 0.9288 | 0.8621 | 0.6177 | 0.4905 | 0.6177 | 0.8621 | 0.9288 | 0.6169 | ||
| 0.02 | 0.3942 | 0.6480 | 0.7186 | 0.6800 | 0.6488 | 0.6800 | 0.7186 | 0.6480 | 0.3942 | ||
| 0.03 | 0.2887 | 0.5067 | 0.6253 | 0.6665 | 0.6733 | 0.6665 | 0.6253 | 0.5067 | 0.2887 | ||
| 0.04 | 0.2331 | 0.4258 | 0.5560 | 0.6251 | 0.6458 | 0.6251 | 0.5560 | 0.4258 | 0.2331 | ||
| 0.05 | 0.1995 | 0.3720 | 0.4996 | 0.5754 | 0.6002 | 0.5754 | 0.4996 | 0.3720 | 0.1995 | ||
| 0.06 | 0.1759 | 0.3315 | 0.4511 | 0.5253 | 0.5504 | 0.5253 | 0.4511 | 0.3315 | 0.1759 | ||
| 0.07 | 0.1574 | 0.2981 | 0.4082 | 0.4778 | 0.5015 | 0.4778 | 0.4082 | 0.2981 | 0.1574 | ||
| 0.08 | 0.1419 | 0.2693 | 0.3698 | 0.4338 | 0.4558 | 0.4338 | 0.3698 | 0.2697 | 0.1419 | ||
| 0.09 | 0.183 | 0.2437 | 0.3351 | 0.3936 | 0.4137 | 0.3936 | 0.3351 | 0.2437 | 0.1283 | ||
| 0.1 | 0.1161 | 0.2208 | 0.3038 | 0.3570 | 0.3753 | 0.3570 | 0.3038 | 0.2208 | 0.1161 |
Величины, полученные методом Кранка-Николсона, достаточно близки к
аналитическому решению u(x,t) = sin(πx)e-π2t+ sin(3πx)e-9π2t, истинные значения для последнего представлены в таблице 2
Максимальная погрешность для данных параметров равна 0,005
Таблица 2 – точные значения u(хi, ti), при t=0.1
| xi | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| t11 | |||||||||||
| 0.1 | 0.1153 | 0.2192 | 0.3016 | 0.3544 | 0.3726 | 0.3544 | 0.3016 | 0.2192 | 0.1153 |
Рисунок 5 –Решение u=u(хi, ti), для метода Кранка-Николсона
ЗАКЛЮЧЕНИЕ
В зависимости от формы области, краевых условий, коэффициентов исходного уравнения метод конечных разностей имеет погрешности аппроксимации от первого до четвертого порядка относительно шага. В силу этого они успешно используются для разработки программных комплексов автоматизированного проектирования технических объектов.
В МКР строятся, как правило, регулярные сетки, особенности геометрии области учитываются только в около граничных узлах. В связи с этим МКР чаще применяется для анализа задач с прямолинейными границами областей определения функций.
Проблемой методов конечных разностей является высокая размерность результирующей системы алгебраических уравнений (несколько десятков тысяч в реальных задачах. Поэтому реализация методов конечных разностей в составе САПР требует разработки специальных способов хранения матрицы коэффициентов системы и методов решения последней.
Библиографический список
1 Березин И.С., Жидков Н.П. Методы вычислений. Т.2. – М.: Физматгиз, 1962.
2 Мэтьюз, Джон, Г., Финк, Куртис, Д. Численные методы. Использование MATLAB, 3-е издание.— М.: Вильяме, 2001. — 720 с
3 Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972.
4 Формалев В.Ф., Ревизников Д.Л. Численные методы. – М.: ФИЗМАТЛИТ, 2004. - 400 с.
5 Пирумов У.Г. Численные методы. – М.: Издательство МАИ, 1998.
6 Калиткин Н.Н. Численные методы. – М.: Наука, 1976.
ПРИЛОЖЕНИЕ А
Листинг программы для расчета по методу Кранка-Николсона
f.m
function F=f(x)
F=sin(pi*x)+sin(3*pi*x);
ft.m
function F=f(x,t)
F=sin(pi*x)*exp(-pi^2*t)+sin(3*pi*x)*exp(-9*pi^2*t);
tisys.m
function X=trisys(A,D,C,B)
N=length(B);
for k=2:N
mult=A(k-1)/D(k-1);
D(k)=D(k)-mult*C(k-1);
B(k)=B(k)-mult*B(k-1);
end
X(N)=B(N)/D(N);
for k= N-1:-1:1
X(k)=(B(k)-C(k)*X(k+1))/D(k);
end
crnich.m
function [U,Y]=crnich(c1,c2,a,b,c,n,m)
clc;
% - c1=u(0,t) и c2=u(a,t)
% - а и b - правые точки интервалов [0,а] и [0,Ь]
% - с - постоянная уравнения теплопроводности
% - n и m - число точек решетки на интервалах [0,а] и [0,Ь]
%Выход - U - матрица решений
%Инициализация параметров и матрицы U
h=a/(n-1);
k=b/(m-1);
r=c^2*k/h^2;
s1=2+2/r;
s2=2/r-2;
U=zeros(n,m);
%Граничные условия
U(1,1:m)=c1;
Продолжение ПРИЛОЖЕНИЯ А
U(n,1:m)=c2;
%Генерирование первого ряда
U(2:n-1,1)=f(h:h:(n-2)*h)';
%Формирование диагональных и не лежащих на диагонали
%элементов А, вектора постоянных В '
%и решение трехдиагональной системы АХ=В
Vd(1,1:n)=s1*ones(1,n);
Vd(1)=1;
Vd(n)=1;
Va=-ones(1,n-1);
Va(n-1)=0;
Vc=-ones(1,n-1);
Vc(1)=0;
Vb(1)=c1;
Vb(n)=c2;
for j=2:m
for i=2:n-1
Vb(i)=U(i-1,j-1)+U(i+1,j-1)+s2*U(i,j-1);
end
X=trisys(Va,Vd,Vc,Vb);
U(1:n,j)=X';
end
U=U';
%точное решение и определение погрешности
x=0:h:h*(n-1);
t=0:k:k*(m-1);
for i=1:1:n
for j=1:1:m
Y(i,j)=ft(x(i),t(j));
end
end
Y=Y';
pogr=(abs(Y-U));
max(max(pogr))
surf(U)
xlabel('X');
ylabel('t');
zlabel('U(x,t)');
colorbar;
axis([0 n 0 m 0 max(max(U))]);