Еще одним наиболее распространенным методом является метод характеристик.
Рассмотрим подробно этот метод.
Метод характеристик
Метод характеристик (англ. Method of characteristics) - метод решения дифференциальных уравнений в частных производных. Обычно применяется к решению уравнений в частных производных первого порядка, но он может быть применен и к решению гиперболических уравнений более высокого порядка. Метод заключается в приведении уравнения в частных производных к семейству обыкновенных дифференциальных уравнений.
Метод заключается в отыскании кривых (именуемых характеристиками), вдоль которых уравнение в частных производных превращается в обыкновенное дифференциальное уравнение. Как только найдены обыкновенные дифференциальные уравнения, их можно решить вдоль характеристик и найденное решение превратить в решение исходного уравнения в частных производных.
Рассмотрим следующее квазилинейное уравнение относительно неизвестной функции
телеграфный уравнение линия передача
.
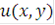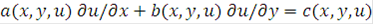(1)
Рассмотрим поверхность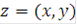 
в R 3. Нормаль к этой поверхности задается выражением:
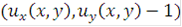
В результате получим, что уравнение (1) эквивалентно геометрическому утверждению о том, что векторное поле:
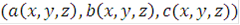
является касательным к поверхности 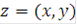в каждой точке.
Также уравнения характеристик могут быть записаны в виде:
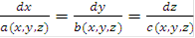
или же, если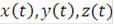 
есть функции параметра t:
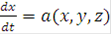
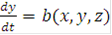
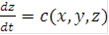
3.2Вывод телеграфных уравнений
Система телеграфных уравнений имеет вид:
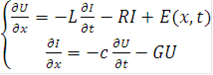(2)
где U, I - значения тока в метеллопокрове и падения напряжения в цепи «металлопокров-земля».
L, R - индуктивность и сопротивление цепи «металлопокров - земля» на единицу длины кабеля.
C, G - емкость и поперечная проводимость цепи «металлопокров - земля».
E(x,t) - распределенный источник ЭДС, численно равный проекции электрического поля на ось линии кабеля.
Единственным допущением при выводе телеграфных уравнений (2) является предположение о том, что поперечный размер оболочки кабеля значительно меньше, чем его продольный размер и характерная длина волны падающего излучения.
Учитывая большие затраты машинного времени на решение уравнений вида (1) на практике применим метод, основанный на решении уравнений (2) в частной или временной областях. В работе показано, что полученное при этом решение с достаточной точностью, соответствующей точному решению уравнения вида (1).
Математическая модель взаимодействия ЭМП с сетью кабельных линий в грунте описывается матричной системой двух телеграфных уравнений вида:
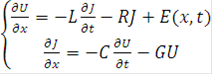(3)
Рассмотрим метод решения системы (3) с заданными граничными условиями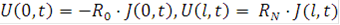 
и нулевыми начальными условиями.
В уравнениях (3) U,J - функции напряжения и тока. Через L,R,C,G - обозначены матрицы индуктивностей, сопротивлений, емкостей, поперечных проводимостей на единицу длины. E(x,t) - функция распределенного источника ЭДС.
Определим зависимость полных дифференциалов друг от друга:
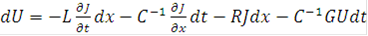
Для дальнейшего преобразования полного дифференциала dU необходимо положить определенные условия на вид сетки конечно-разностной схемы.
Предположим, что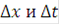 
связаны соотношениями:
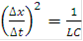
Тогда при движении из точки (i,n) сетки в точку (i+1/2,n+1/2) на прямой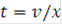 
выполняется соотношение:
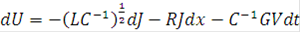
При движении из точки (i+1,n) в точку (i+1/2,n+1/2) на прямой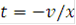 
выполняется соотношение:
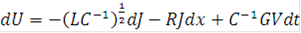
Значения конечно-разностных аналогов функции J и V на полуцелом слое по времени при этом определяется следующим образом:
; 
.
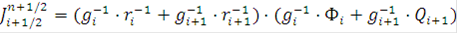
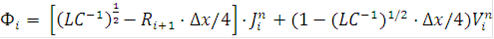
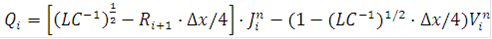
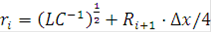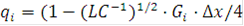При известных значениях сеточных аналогов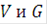 
полуцелом слое систему (3) можно записать в виде:
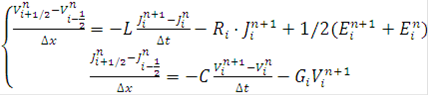(4)
Уравнения (4) разрешимы относительно относительно переменных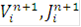 
. Тем самым определены значения функций 
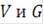на любом временном слое, если заданы граничные и начальные условия.
Данный метод решения носит название метод характеристик.
В уравнении (3) векторные функции тока и напряжения имеют N составляющих. При этом k-ая составляющая соответствует току и напряжению в цепи «металлопокров-земля». Матрицы L,R,C,G имеют размерность N 
N. Диагональные матрицы равны соответствующим параметрам одиночной линии (жила), а недиагональные члены характеризуют взаимное влияние параллельных кабелей (жил).
Элементы матриц могут быть заданы на основе эспериментально определяемых параметров.
В случае, если таковые отсутствуют, элементы матрицы индуктивностей рассчитываются по соотношению:
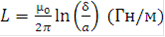
где 
- собственный радиус кабеля (жилы).
δ - параметр, равный среднему значению толщины скин - слоя в грунте (внутреннему диаметру металлопокрова кабеля).
Матрица индуктивностей определяет матрицу емкостей:
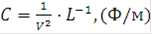
Матрица поперечных проводимостей описывается через матрицу емкостей:
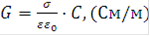
где σ и ε - проводимость и диэлектрическая проницаемость окружающего кабель грунта (внутреннего диэлектрика кабеля).
Заключение
В ходе проделанной работы можно сделать следующие выводы:
. Выведены телеграфные уравнения во временном представлении для однородной однопроводной линии, расположенной в проводящей однородной среде и подверженной воздействию импульсного однородного электромагнитного поля.
2. Показано, что в зависимости от способа определения напряжения в линии можно использовать два варианта исходных уравнений, описывающих наведенные в линии токи и напряжения.
. Представлена конечно - разностная схема для численного решения телеграфных уравнений и приведены примеры численных расчетов.
Список использованной литературы
1. Бессонов Л. А. «Теоретические основы электротехники»
2. Фальковский О. И. «Техническая электродинамика»
. Бахвалов Н. С. «Численные методы»
. Самарский А. А. «Введение в численные методы»
. Попов В. С. «Электротехника»
. Савельев И. В. «Электричество»
. Иродов И. Е. «Электромагнетизм. Основные законы»
. Кузнецов М. И. «Основы электротехники»