Лекция
По дисциплине «Инженерная графика»
Раздел. 1 Начертательная геометрия
Составитель: Шагвалеева.Г.Н.
Введение.
Начертательную геометрию называют также теорией изображений. Предметом начертательной геометрии является изложение и обоснование способов изображения пространственных фигур на плоском чертеже и способов решения пространственных геометрических задач на плоском чертеже. Стереометрические (трехмерные) объекты обсуждаются в ней с помощью планиметрических (двухмерных) изображений этих объектов, проекций.
Говорят, что чертеж – язык техники, а начертательная геометрия – грамматика этого языка. Начертательная геометрия является теоретической основой построения технических чертежей, которые представляют собой полные графические модели конкретных инженерных изделий.
Правила построения изображений, излагаемых в начертательной геометрии, основаны на методе проекций.
Изучение начертательной геометрии способствует развитию пространственного представления и воображения, конструктивно геометрического мышления, развитию способностей к анализу и синтезу пространственных форм и отношений между ними. Освоению способов конструирования различных геометрических пространственных объектов, способов получения их чертежей на уровне графических моделей и умению решать на этих чертежах задачи, связанные с пространственными объектами и их геометрическими характеристиками.
Основание начертательной геометрии как науке было положено французским ученым и инженером Гаспаром Монжем (1746-1818) в его труде “Начертательная геометрия”, Париж, 1795 г. Гаспар Монж дал общий метод решения стереометрических задач геометрическими построениями на плоскости, то есть на чертеже, с помощью чертежных инструментов.
|
|
Принятые обозначения.
А, В, С, D, -точки обозначаются заглавными буквами латинского алфавита;
a, b, с, d - линии - строчными буквами латинского алфавита;
p1 – горизонтальная плоскость проекций,
p2 – фронтальная плоскость проекций,
p3 - профильная плоскость проекций,
p4, p5,... - дополнительные плоскости проекций.
, 
, 
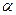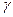- плоскости
Оси проекций - строчными буквами латинского алфавита: х, y и z. Начало координат - цифрой 0.
Проекции точек, прямых, плоскостей обозначаются: на p1 с одним штрихом, на p2 с двумя, на p3 – с тремя штрихами.
p1 – АI, ВI, CI,..., aI, bI,...,a I, bI,
p2 – АII, ВII, CII,..., aII, bII,...,a II, bII,
p3 – АIII, ВIII, CIII,..., aIII, bIII,...,a III, bIII.
Образование проекций.
1 Центральное проецирование.
Аппарат центрального проецирования состоит из центра проецирования S, плоскости проекций π, проецирующих лучей.
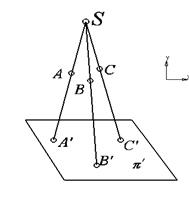
π1 - плоскость проекций
S – центр проецирования
A, B, C - точки в пространстве
A', B', C' - проекции точек на плоскость π'
Рис.1.1
Проекция – это точка пересечения проецирующего луча с плоскостью проекций.
2. Параллельное проецирование.
Проецирующие лучи проводятся параллельно S и друг другу. Параллельные проекции делятся на косоугольные и прямоугольные. При косоугольном проецировании лучи расположены под углом к проецирующей плоскости.
Рис. 1.2
.
При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (рис. 1.3). Прямоугольное проецирование является основным способом проецирования, принятым при построении технических чертежей
|
|
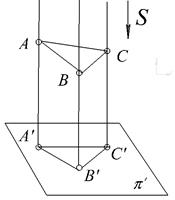
Рис. 1.3.
Основные свойства ортогонального проецирования
1. Проекция точки - есть точка;
2. Проекция прямой (в общем случае) – есть прямая линия или точка(прямая перпендикулярна плоскости проекций);
3. Если точка лежит на прямой, то проекция этой точки будет принадлежать проекции прямой: А 
l ® A' l';
4. Если две прямые в пространстве параллельны, то их одноименные проекции также параллельны: a || b ® a` || b`;
5. Если две прямые пересекаются в некоторой точке, то их одноименные проекции пересекаются в соответствующей проекции этой точки: m ∩ n = K ® m' ∩ n' = K';
6. Пропорциональность отрезков, лежащих на одной прямой или на двух параллельных прямых, сохраняется и на их проекциях (рис.1.3): АВ:СD = А'B': C'D'
7. Если одна из двух взаимно перпендикулярных прямых параллельна плоскости проекций, то прямой угол проецируется на эту плоскость прямым углом (рис.1.4).
Рис.1. 4.
Комплексный чертеж точки или эпюр Монжа.
Самый употребительный на практике метод начертательной геометрии предложил Гаспар Монж. В основе этого метода лежит ортогональное проектирование.
Ортогональной (или прямоугольной) проекцией точки А на плоскость π1 называют основанием перпендикуляра, опущенного из точки А на плоскость π1 (рис.1.5)
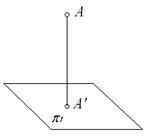
Рис. 1.5
Получаемый при этом на плоскости π1 чертеж необратим, соответствие между оригиналом А и проекцией A' однозначно только в одну сторону: от оригинала к проекции. Оригиналу соответствует единственная проекция, оригиналом чертеж определен однозначно, но для проекции A' существует бесчисленное множество соответствующих ей оригиналов, а именно все точки проецирующей прямой A A'. Точный перевод с языка чертежа на язык натуры невозможен. Поэтому Монж вводит вторую плоскость проекций.
|
|
Рис. 1.6. Рис.1. 7.
На рис. 6. изображена прямоугольная система координат.
Совмещая теперь плоскости π1 и π2 с построенными в них проекциями поворотом π1 вокруг оси Х на 900 так, чтобы передняя полуплоскость π1 совпала с нижней полуплоскостью π2, получаем комплексный чертеж точки или эпюр Монжа. (рис. 1.7).
Построенный по таким правилам чертеж, состоящий из пары проекций, расположенных в проекционной связи, обратим, то есть соответствие между оригиналом и чертежом однозначно в обе стороны. Или иначе говоря, чертеж дает исчерпывающую информацию об оригинале. Расшифровка этой информации и составляет предмет начертательной геометрии.
Из комплексного чертежа точки можно сделать выводы:
1. две проекции точки вполне определяют положение точки в пространстве;
2. проекции точек всегда лежат на линии связи, перпендикулярной оси проекции.
A' A" 
Х
Линии, соединяющие проекции точек, называются линиями связи и изображаются сплошными тонкими линиями.
В ряде построений и при решении задач оказывается необходимым вводить в систему π1 (горизонтальная плоскость) π2 (Фронтальная плоскость) и другие плоскости проекций. Плоскость, перпендикулярная и к π1 и к π1, - это профильная плоскость. π3. Линия пересечения горизонтальной и фронтальной плоскостей дают ось Х, линия пересечения горизонтальной и профильной плоскостей дают ось У, и линия пересечения фронтальной и профильной плоскостей – ось Z. (рис.1. 8)
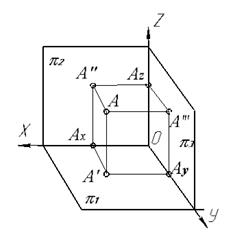
Рис. 1.8
Чтобы получить комплексный чертеж точки необходимо расположить три плоскости в одной, для чего «разрезаем» ось У и совмещаем три основные плоскости проекций в одну (рис.1. 9).
Рис. 1.9
Новой информации об оригинале третья проекция не добавляет. Она лишь делает имеющуюся информацию более удобоваримой. (Рис. 1.10)
Рис. 1.10
Расстояние от точки А до плоскости π3 (А A"') в пространстве можно увидеть на чертеже и оно равно расстоянию A'AY = A"AZ = AX0 = X
Расстояние от точки А до плоскости π2 (А A") в пространстве можно увидеть на чертеже и оно равно расстоянию A'AX = A"'AZ = AY0 = Y
Расстояние от точки А до плоскости π1 (А A') в пространстве можно увидеть на чертеже и оно равно расстоянию A"AX = A"'AY = AZ0 = Z
Пример. Построить проекции точек А(10, 10,30), В(30,20,10)
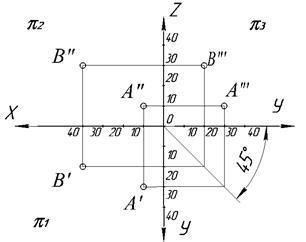
Рис.1.11
Конкурирующие точки.
Точки, у которых совпадает одна пара одноименных проекций (а другие не совпадают), называются конкурирующими точками.
Понятие «ближе-дальше »
Точки расположены на одной проецирующей прямой, перпендикулярной фронтальной плоскости проекций. Направление взгляда указано стрелкой. При этом проекция B' ближе к наблюдателю, чем A', и на π2 видимой будет проекция B'' а проекция А'' будет невидимой (рис. 1.12).
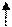
Рис. 1.12
Понятие «выше-ниже »
Точки расположены на одной проецирующей прямой, перпендикулярной горизонтальной плоскости проекций. Направление взгляда указано стрелкой. При этом проекция А'' ближе к наблюдателю, чем В'', и на π1 видимой будет проекция А' а проекция В' будет невидимой (рис. 1.13).
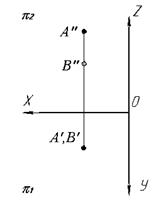
Рис. 1.13
Чем дальше проекция точки от оси Х, тем точка выше или ближе к наблюдателю.