Метод уточнения нелинейного уравнения методом касательных.
Выберем начальную точку x0=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Х дает нам первое приближение корня x1.

Рис. 4.8.
x1 = x0 – h0,
где

Поэтому

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой
 (4.6)
(4.6)
Процесс поиска продолжаем до тех пор, пока не выполнится условие:
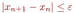 (4.7)
(4.7)
Упростим условие (4.7), исходя из (4.6). Получим:
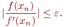
Метод обеспечивает быструю сходимость, если выполняется условие:

т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x0)и ее кривизны f"(x0)совпадают.
Метод уточнения нелинейного уравнения методом простых итераций.
Дано нелинейное уравнение 𝑓(𝑥) = 0. Корень отделен и лежит в интервале [a;b]. Требуется уточнить корень с точностью ε.
Уравнение 𝑓(𝑥) = 0 преобразуем к эквивалентному виду 𝑥 = 𝜑(𝑥). Это можно сделать всегда и притом множеством способов. Выберем начальное приближение x0Î[a;b]. Вычислим новые приближения: 𝑥1 = 𝜑(𝑥0), 𝑥2 = 𝜑(𝑥1)… 𝑥𝑖 = 𝜑(𝑥𝑖−1) (1) i=1,2,… где i − номер итерации. Последовательное вычисление значений xi по формуле (1) называется итерационным процессом метода простых итераций, а сама формула - формулой итерационного процесса метода. Теорема. Пусть на [a,b] имеется единственный корень уравнения 𝑥 = 𝜑(𝑥) и во всех точках отрезка [a,b] 𝑓′(𝑥) удовлетворяет неравенству 𝜑′(𝑥) <1. Если при этом выполняется и условие 𝑎 ≤ 𝜑(𝑥) ≤ 𝑏, то итерационный процесс сходится, а за нулевое приближение 𝑥0 можно взять любое число из отрезка [a,b]. Условие сходимости 𝜑′(𝑥) < 1 ∀𝑥 ∈ [𝑎, 𝑏] Точное решение x* получить невозможно, так как требуется бесконечный итерационный процесс. Можно получить приближенное решение, прервав итерационный процесс при достижении условия |𝑥𝑖+1 – 𝑥𝑖| ≤ 𝜀 где 𝜀- заданная точность; i - номер последней итерации. Рекомендуется следующий способ получения формулы сходящегося итерационного процесса. Пусть 𝑓′(𝑥) > 0 ∀ 𝑥 ∈ 𝑎, 𝑏. Если это не так то переписать уравнение в виде –𝑓(𝑥) = 0. Умножить обе части уравнения на 𝜆 (𝜆 > 0) и к обеим частям прибавить 𝑥: 𝑥 = 𝑥 – 𝜆𝑓(𝑥) = 𝜑(𝑥). Константу 𝜆 вычислить по формуле 𝜆 = 1/max 𝑥∈ 𝑎,𝑏 |𝑓′(𝑥)| Такое значение 𝜆 гарантирует сходящийся итерационный процесс по формуле 𝑥𝑖 = 𝑥𝑖+1 − 𝜆𝑓(𝑥).
Метод уточнения нелинейного уравнения методом деления отрезка пополам.
Дано нелинейное уравнение ¦(x) = 0. Пусть корень отделен, т.е. известно, что x* Î [a,b]. Требуется вычислить корень с заданной точностью ε. Суть метода - постепенное уменьшение отрезка существования корня, используя факт изменения знака функции в окрестности корня. Алгоритм метода: Вычислить координату середины отрезка [a,b] x = (a+b)/2 и значение ¦(x) в этой точке. Уменьшить отрезок, отбросив ту его половину, на которой корня нет. Если знак функции в начале отрезка и в его середине одинаков, то корень находится на второй половине, первую половину можно отбросить, переместив начало отрезка в его середину: если ¦(a) ·¦(x)>0 => x* Î [x,b] => a=x, иначе x * Î [a, x] => b=x Проверить условие завершения вычислений: длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью: b-a ≤ ε ∩ |¦(x)| ≤ ε. Если условие достигнуто, расчет завершен, иначе повторить алгоритм сначала. Количество итераций n, требуемых для достижения требуемой точности ε можно оценить заранее из соотношения
𝜀 = (𝑏 – 𝑎)\2 ⇒ 𝑛 = ln((𝑏 − 𝑎)/𝜀)/𝑙𝑛2.