Таблица № 7.
Средние кластеры
| н.о.1 | н.о.2 | н.о.3 | н.о.4 | |
| с_1 | 80,54000 | 10,20000 | 3,160000 | 0,468571 |
| с_2 | 63,07000 | 17,42000 | 3,390000 | 1,704286 |
| с_3 | 66,34000 | 18,60000 | 2,310000 | 1,308571 |
| с_4 | 66,59000 | 16,86000 | 3,610000 | 1,335714 |
| с_5 | 69,53000 | 14,17000 | 3,245000 | 1,312857 |
| с_6 | 75,84000 | 13,32000 | 4,365000 | 0,310000 |
| с_7 | 76,28000 | 12,93000 | 3,725000 | 0,467143 |
| с_8 | 72,06000 | 14,96000 | 3,980000 | 0,668571 |
| с_9 | 72,95000 | 15,10000 | 3,555000 | 0,624286 |
| с_10 | 74,79000 | 14,19000 | 2,625000 | 0,851429 |
| с_11 | 72,90000 | 13,00000 | 3,490000 | 0,924286 |
| с_12 | 76,00000 | 13,35000 | 2,180000 | 0,918571 |
| с_13 | 75,81500 | 12,48300 | 3,162500 | 0,732571 |
| с_14 | 72,66700 | 16,30300 | 2,661500 | 0,810429 |
| с_15 | 75,61100 | 12,89900 | 4,364500 | 0,375714 |
| с_16 | 73,23800 | 13,62500 | 3,299500 | 0,880571 |
| с_17 | 74,98400 | 14,83700 | 4,254500 | 0,142714 |
| с_18 | 75,12600 | 13,33600 | 4,996500 | 0,179571 |
| с_19 | 76,76100 | 13,14900 | 4,655000 | 0,082571 |
| с_20 | 78,06200 | 13,08200 | 3,858000 | 0,117143 |
| с_21 | 74,83900 | 14,18700 | 4,328500 | 0,224143 |
| с_22 | 73,64000 | 14,11900 | 4,629000 | 0,264286 |
| с_23 | 74,98300 | 14,11700 | 4,098000 | 0,194143 |
| с_24 | 76,31700 | 12,99600 | 4,364000 | 0,180714 |
| с_25 | 73,61100 | 14,26300 | 4,898000 | 0,211143 |
| с_26 | 67,49700 | 15,21700 | 4,499000 | 0,754571 |
| с_27 | 76,39100 | 13,82400 | 3,840500 | 0,199714 |
| с_28 | 77,41300 | 12,92700 | 3,815500 | 0,213000 |
| с_29 | 77,91000 | 12,79600 | 3,997000 | 0,116143 |
| с_30 | 75,76600 | 13,16200 | 4,086000 | 0,275857 |

Рисунок 9 - Дендрограмма горизонтальной связи
Таблица № 8.
Евклидовы расстояния между кластерами
| н.о.1 | н.о.2 | н.о.3 | н.о.4 | |
| н.о.1 | 0,00000 | 3612,168 | 4932,947 | 5398,391 |
| н.о.2 | 60,10131 | 0,000 | 109,094 | 183,818 |
| н.о.3 | 70,23494 | 10,445 | 0,000 | 11,482 |
| н.о.4 | 73,47375 | 13,558 | 3,389 | 0,000 |
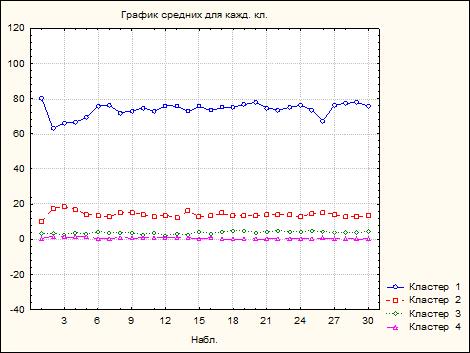
Рисунок 10 - График средних для каждого кластера
Факторный анализ
С возрастанием количества анализируемых признаков быстро растет трудность изучения и классификации характеризуемых ими объектов. Между тем, любые сложнопостроенные системы, как правило, управляются сравнительно небольшим набором факторов. Выявлению и анализу этих факторов посвящен широкий круг вычислительных процедур, обычно объединяемых названием «факторный анализ». Следует однако, помнить, что в названной области выделяется несколько самостоятельных процедур: метод главных компонент (МГК), R–метод факторного анализа, Q–метод факторного анализа, анализ главных координат, анализ соответствия. Все эти методы основаны на выделении собственных значений и собственных векторов ковариационной или корреляционной матрицы, поскольку заранее предполагается, что в наборе многомерных наблюдений скрыта простая структура, выражающаяся через дисперсии и ковариации переменных.
Метод главных компонент позволяет выявить группы элементов, наиболее тесно связанных с тем или иным мощным фактором. Элементы, однонаправлено изменяющие свое состояние под действием общего фактора, могут быть объединены в комбинации, называемые главными компонентами. Число последних намного меньше исходного числа параметров, в то же время они несут практически всю полезную информацию об изменчивости свойств, заключенную в исходной совокупности.
Главные компоненты вычисляются по формулам:
1ГК = ∑ωilxi = ω1l ·х1 + ω1х2 +.... +ωn1хn;
2ГК = ∑ωi2xi;
3ГК = ∑ωi3xi и т.д..
Здесь xi - значения параметров, ωij - факторные нагрузки (это влияние j -го фактора на i -й элемент, т.е. своего рода коэффициент корреляции между ними).
Таким образом, для нахождения главных компонент нам необходимо вычислить матрицу факторных нагрузок W. Она определяется из соотношения:
W = uΛ½
где u - матрица собственных векторов, а Λ - матрица собственных чисел корреляционной матрицы R. Элементы матрицы Λ определяются как корни характеристического уравнения:
|R-λ׀| = 0, где I - единичная матрица.
Вычислив этот определитель, получаем уравнение, степень которого и число полученных корней равны числу строк в корреляционной матрице R. При этом λ1 >λ2 >λ3... >λn, a ∑λi = n. Матрица u, находится из выражения:
(R - λ1)u=0
Подставляя в это уравнение найденные значения λi, получаем для каждого λi вектор значений ui.
Таблица №9. Факторные нагрузки
| фактор 1 | фактор 2 | |
| SiO2 | 0,910032 | 0,180100 |
| TiO2 | -0,728842 | -0,516303 |
| Al2O3 | -0,759301 | -0,238498 |
| Fe2O3 | -0,908964 | 0,064969 |
| MnO | -0,780036 | 0,211023 |
| MgO | -0,656868 | 0,309249 |
| CaO | -0,618584 | 0,521466 |
| Na2O | -0,040191 | -0,699149 |
| K2O | 0,635565 | -0,052068 |
| P2O5 | -0,699322 | -0,455301 |
| ППП | -0,821456 | 0,347351 |
| Общ.дис. | 5,754100 | 1,591671 |
| Доля общ | 0,523100 | 0,144697 |

Рисунок 11 – Диаграмма факторных нагрузок
Как видим, 1-й фактор значимо влияет на все элементы. Такой фактор обычно называют генеральным. Генеральный фактор отрицательно сказывается на контрастности корреляционной матрицы, обуславливая перекрытие выделяемых групп. Дать главным факторам геологическую интерпретацию не всегда возможно, но когда это удается, информативность метода резко возрастает. В частности, в рассмотренном примере со 2-м фактором, видимо, связан процесс карбонатизации пород. Дать интерпретацию 1-му фактору сложнее.
Метод главных компонент можно использовать и для распознавания образов. Для этого в координатах двух ГК выносятся значения для эталонных объектов и локализуются области, отвечающие этим объектам
Таким образом МГК сводится к линейному преобразованию М исходных переменных в т новых переменных, каждая из которых является линейной комбинацией исходных переменных. При этом МГК не является статистическим методом и мы практически не имеем формальных критериев для отбрасывания некоторых переменных или компонент, дающих очень малый вклад в суммарную дисперсию. О правильности своих действий мы можем судить только после проведения анализа МГК.

Рисунок 12 - Определение промышленного типа месторождения по методу главных компонент.
а - 1-й промтип, б - 2-й промтип, в – непромышленнные объекты, г - изучаемое рудопроявление.
В отличие от МГК, факторный анализ считается статистическим методом, поскольку в его основе лежат некоторые предположения о природе изучаемой совокупности. Предполагается, что связь между m переменными является отражением корреляционной зависимости каждой из переменных с р взаимно некоррелированными факторами, причем р<m (если р = m, модель эквивалентна МГК). Поэтому дисперсию для m переменных можно вычислить с помощью дисперсии р – факторов плюс вклад, происхождение которого одинаково для всех переменных.
В Q-методе факторного анализа, в отличие от R-метода, анализируются взаимосвязи между наблюдениями, а не переменными.
Одно из главных препятствий в применении геологами различных модификаций факторного анализа заключено в абстрактности понятий собственных векторов и собственных значений корреляционных матриц. Между тем, эти категории имеют вполне определенный содержательный и геометрический смысл. На рис. видно, что строки корреляционной матрицы можно представить как произвольные оси двумерного эллипсоида, тогда собственные вектора, дают направление главных осей эллипсоида, а корень из величины собственного значения – длину главных полуосей. Поскольку собственные значения включают в себя дисперсии переменных, очевидно, что и факторы отражают дисперсии (точнее, стандартные отклонения). При этом наклон и длина главных осей эллипсоида наглядно свидетельствуют о влиянии фактора на значения конкретной переменной.

Рисунок 13 - Графическое изображение собственных векторов корреляционной матрицы.
Поскольку одна из главных задач факторного анализа - сокращение размерности исходного пространства признаков, важнейшим вопросом является выбор количества сохраненных факторов. Формального ответа на этот вопрос не существует, поэтому в большинстве случаев рекомендуется сохранять столько факторов, сколько имеется собственных чисел, больших 1, то есть сохраняются факторы, вклад которых в дисперсию больше, чем у каждой из исходных переменных. Эта рекомендация полезна в тех случаях, когда исходные данные хорошо скоррелированы и первые 2-3 фактора дают основной вклад в общую дисперсию. Если же переменные скоррелированы слабо, то половина и даже больше факторов может иметь собственные числа большие единицы. Число факторов получается слишком большим, причем вклад каждого из них в дисперсию невелик, а содержательная интерпретация затруднительна. В таких случаях применение факторной модели следует признать нецелесообразным.
В ряде случаев бывает затруднительно дать интерпретацию факторов даже если переменные хорошо скоррелированы. Перекрытие групп переменных зачастую обусловлено тем, что положение р ортогональных факторных осей в m-мерном пространстве определяется положением m–р ненужных ортогональных осей в выборочном пространстве. Исключив из рассмотрения ненужные оси, мы можем произвести вращение оставшихся факторных осей таким образом, чтобы выделенные группы наилучшим образом расположились в новых координатах. В наиболее часто используемом методе (метод варимакс Кайзера) вращение осуществляется до тех пор, пока проекции каждой переменной на факторные оси не окажутся близкими либо к нулю, либо к ±1. Чаще всего такое вращение приводит к тому, что для каждого фактора мы получаем несколько больших значений нагрузок и много близких к нулю. Это существенно облегчает содержательную интерпретацию факторов. Если же вращение факторных осей лишь ухудшает первоначальный результат, это свидетельствует либо о взаимной коррелированности факторов, либо о неприменимости выбранной факторной модели.
Графическое представление процедуры вращения факторных осей для двумерного случая дано на рис..

Рисунок 14 - Вращение факторных осей для двумерного случая.
Проекции векторов переменных на факторные оси соответствуют их факторным нагрузкам. Видно, что после вращения разделение элементов на группы значительно улучшилось. При этом длина векторов и их относительное положение не изменились.
Таким образом, факторный анализ сочетает в себе преимущества и возможности как методов группирования, так и распознавания образов. В частности, он может быть использован как вариант множественной регрессии для вычисления восстановленных значений переменной:
Хвост. = S⋅ωj⋅Z′j+х⋅ε΄,
где S – диагональная матрица m х m оценок стандартов m переменных;
ωj – факторная нагрузка j фактора;
Z´j – вектор-строка значений фактора j;
х - среднее значение параметра по выборочным данным;
ε΄ -вектор-строка размером N (число наблюдений) вида {1, 1, 1,.... 1}.
Таким способом можно оценить влияние каждого выделенного фактора (процесса) на распределение конкретного элемента и геометризовать в пространстве интенсивность этого влияния. Эта задача обычна при создании генетических моделей и прогнозо-поисковых комплексов.
Заключение
Данная контрольная работа, основной целью, которой было выяснить и понять распределение полезных компонентов в гранитах Восточного Забайкалья, по данным полученным в результате опробования и проведения рентгенофлуоресцентного анализа проб, содержит в себе результаты проведения анализов в программе «Statistica», с составлением таблиц и графических диаграмм.
Было проведено 6 анализов:
1. Статистический анализ – анализ с помощью, которого были получены статистические характеристики для каждого компонента, которые образуют гранитные породы (SiO2. TiO2, Al2O3, Fe2O3, MnO, MgO, CaO, Na2O, K2O, P2O5, ППП), представленные в таблице 2.
2. Корреляционный анализ – анализ, заключался в изучении коэффициентов корреляции между переменными, в результате, которого была создана таблица корреляции по всем элементам (таблица 3), где явно прослеживалась линейная взаимосвязь, на основании, которой были представлены диаграммы рассеяния (рисунок 6).
3. Регрессионный анализ – анализ, смысл которого, заключался в построении зависимостей между группами числовых переменных; в результате анализа была составлена таблица предсказанных значений и остатков, с зависимой переменной TiO2 и MgO, на основании, которой был составлен нормальный вероятностный график остатков, который наглядно показывает отсутствие больших отклонений от высказанных предположений.
4. Кластерный анализ – ряд методов, который использовался для группировки объектов в кластеры на основе сходства их характерных признаков; в результате анализа «иерархическая классификация» были составлены дендрограммы горизонтальные и вертикальные, которые показывают степень близости кластеров, и последовательность их объединения и разделения, где в нашем случае наиболее дальше расположен элемент SiO2.
Было выявлено 4 кластера, на основании, которых были построены таблицы описательных статистик для каждого кластера, и для каждого кластера было выявлено содержание элементов в каждом из них, и составлен график средних для каждого кластера, где явно видна степень активности кластера 1 (SiO2), как самостоятельного элемента, процентное содержание, которого относит г/п к одному из классов магматических горных пород.
5. Факторный анализ – проведение анализа заключалось в выявлении влияния факторных нагрузок на элементы, в результате, чего была составлена таблица факторных нагрузок, и диаграмма факторных нагрузок, на котором явно прослеживается сосредотачивание группы элементов или их присутствие по отдельности.
В результате проведения всех анализов, можно предположительно сделать вывод о том, что результаты рентгенофлуоресцентного анализа верны, и содержание элементов, которые образуют 1 тип пород (граниты) правильны, что доказывает проведение статистических анализов, которые являются неточными, но характер поведения элементов показали явно.