МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ПРОВЕДЕНИЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ
Направление подготовки бакалавра 20.03.01 «Техносферная безопасность»
Профиль «Пожарная безопасность»
по учебной дисциплине «Высшая математика»
Тема № 4. Неопределенный интеграл.
Занятие 4.2. Вычисление интегралов (Часть I).
Учебная группа: 121 - 124.
Обсуждена на заседании
методической секции «Высшая математика»
Протокол № 12 от «31» июля 2014 года
I. Цели и задачи занятия
1. Выработать навыки интегрирования (непосредственное интегрирование).
2. Воспитывать у обучающихся стремление к углубленному освоению материала по теме занятия, расширению профессионального кругозора, обучению методам самостоятельной работы с первоисточниками и учебными материалами.
3. Проверить качество усвоения обучающимися учебного материала.
II. План проведения и расчет учебного времени
| Содержание и порядок проведения занятия | Время, мин |
| ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы: 1. Неопределенный интеграл и его свойства. 2. Вычисление интегралов непосредственным интегрированием. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ |
III. Учебно-материальное обеспечение
Классная доска, раздаточный материал, плакат с таблицей интегралов, планшет, видеопроектор, экран.
IV. Методические материалы
К проведению практического занятия
Во вводной части занятия (5 мин) после объявления темы и целей практического занятия целесообразно изложить последовательность обсуждения учебных вопросов.
Первый учебный вопрос (10 мин).
Неопределенный интеграл и его свойства.
Функция 
называется первообразной функции 
на интервале 
, если для любого 
выполняется равенство 
.
Если функция является первообразной функции на , то множество всех первообразных для задается формулой 
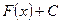, где 
.
Множество всех первообразных функций 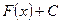для называется неопределенным интегралом от функции и обозначается символом 
.
Здесь называется подынтегральной функцией, 
– подынтегральным выражением, 
– переменной интегрирования,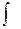 
– знаком неопределенного интеграла.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых 
(каждому числовому значению С соответствует определенная кривая семейства). График каждой первообразной (кривой) называется интегральной кривой.
Свойства неопределенного интеграла:
1. 
; 
;
2. 
;
3. 
, 
;
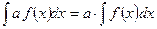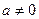4. 
;
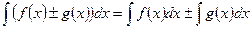5. Если , то и 
, где 
– произвольная функция, имеющая непрерывную производную.
Таблица основных интегралов
1.  ;
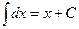| 2.  ;
|
3.  ;
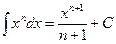| 4.  ;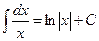
|
5.  ;
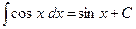| 6.  ;
|
7.  ;
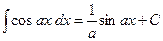| 8.  ;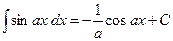
|
9.  ;
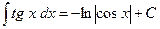| 10.  ;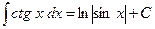
|
11.  ;
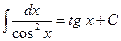| 12.  ;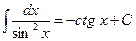
|
13. 
| 14.  ;
|
15.  ;
| 16.  ,  ;
|
17.  ;
| 18.  ,  ;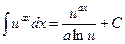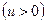
|
19.  ;
| 20.  ;
|
21.  ;
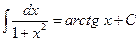| 22.  ;
|
23.  ;
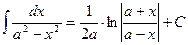| 24.  .
|
Второй учебный вопрос (70 мин).
Вычисление интегралов непосредственным интегрированием.
Решение упражнений:
№ 1. Применяя метод непосредственного интегрирования, вычислить интегралы.
Решение:
1. 
;
2. 
;
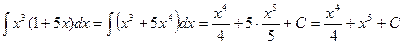3. 
;
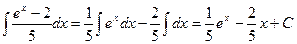4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
10. 
;
11. 
.
№ 2. Скорость точки, движущейся прямолинейно, задана уравнением 
. Найдите закон движения точки, если за время 
она пройдет путь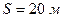 
.
Решение:
; 
.
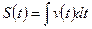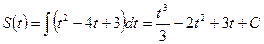Подставим условия: 
=> 
Закон движения точки: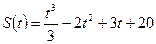 
.
В заключительной части (5 мин) преподаватель подводит итоги и завершает работу практического занятия, давая оценку ходу занятия и работе отдельных обучающихся, ставя задачи на дальнейшее изучение учебной дисциплины. Здесь же необходимо дать характеристику последующих тем, указав, где будут использоваться обсужденные материалы, выдать задание на следующее занятие.