
( +(
+( *
* 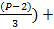 ...
...  (
( *
* 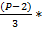 ...
... 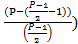 =
=  ? N
? N
В зависимости от количества уникальных биномиальных коэффициентов 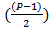 , количество элементов, оказывающих влияние на итоговый результат проверки числа на простоту, растёт. Количество которых равно, количеству уникальных биномиальных коэффициентов
, количество элементов, оказывающих влияние на итоговый результат проверки числа на простоту, растёт. Количество которых равно, количеству уникальных биномиальных коэффициентов 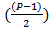
1+( +(
+( *
* 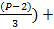 ...
...  (
( *
* 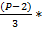 ...
... 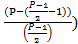 =
= 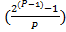 ? N
? N
 =
= 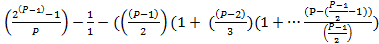
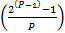 –
–  = 0
= 0 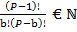
Т.е. Количество элементов, переносимых в правую часть уравнения, для сохранения истинности теста простоты, равняется 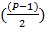 .
.
Рассмотрим несколько простых чисел P=3;5
Для P=3
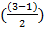 =1
=1
 *
* 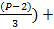 ...
...  (
( *
* 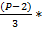 ...
... 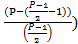 =
=  = 0
= 0
Для P=5
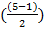 =2
=2
 (
( *
* 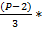 ...
... 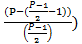 =
=  = 0
= 0
Зная число вычитаемых элементов, для обнуления уравнения, найдем (P(п)) - число проходящее тест простоты
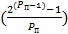 =
= 
Поскольку количество вычитаемых элементов равно, количеству уникальных биномиальных коэффициентов, перепишем формулу.
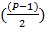 = b
= b
2b + 1=P(п)
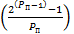 =
=  =1+(
=1+( ) + (
) + ( ) +…
) +…
Выведем формулу максимального значения уникального коэффициента. Где b – порядковый номер, исследуемого, потенциального простого числа. Где q – порядковый номер, исследуемого, коэффициента, за исключением единицы (Счёт идёт от коэффициента стоящего при меньшей степени).
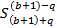 =
= 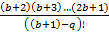
Найдём сумму всех уникальных коэффициентов.
 =
= 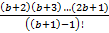 +
+  ...+
...+ 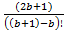
Разделим сумму, всех уникальных коэффициентов, за исключением единицы, на второй коэффициент.
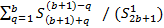 =
= 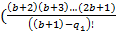 +
+  ...+
...+ 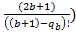 /
/ 
Исходя из правила деления дробей, перепишем формулу.
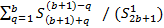 =
= 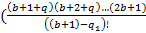 +
+  ...+
...+ 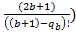 *
* 
Для удобства, разделим каждый коэффициент на второй обособленно, лишь затем сложим результаты.
Отношение третьего коэффициента ко второму.
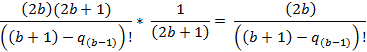
Отношение четвертого коэффициента ко второму.

Отношение максимального коэффициента ко второму.
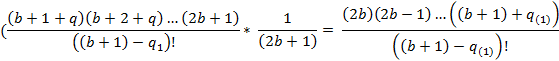
На данном этапе видно, что для некоторых b, порядковых номеров потенциального простого числа, не существует целого решения. Но при этом, сумма всех коэффициентов,
для b, порядковый номер, скрывающий за собой псевдо-простое число, такое решение имеется, в силу взаимной компенсации дробных частей.
Выведем общую формулу сумм отношений уникальных коэффициентов, за исключением первого.
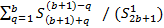 =
= 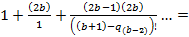
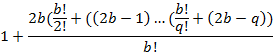
Определим количество b, порядковых номеров потенциального простого числа, для которых не существует целого решения.
Заменим операцию деления, на операцию умножения, путём представления частного дробью вида 1/ x.
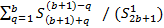 =
=
(
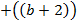 )) *
)) * 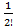
Полученное частное, в лимитированном виде, является разложением в ряд Тейлора числа (e) с вычетом единицы, равняющееся ~ 1, 7182818284…
Lim(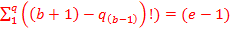 =1, 7182818284…
=1, 7182818284…
Т.е. лимитированное отношение суммы всех уникальных коэффициентов, за исключением единицы, на второй коэффициент.
Lim(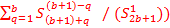 =
=
(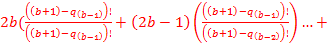
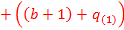 ))
)) 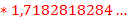
Определим количество b, порядковых номеров потенциального простого числа, для которых не существует целого решения.
Определим элементы, заведомо сократимые на наименьший коэффициент.
 =
=  +
+  + …
+ … 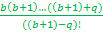
Для этого приведем дроби к общему знаменателю.

Поскольку при делении на наименьший коэффициент, знаменатели данной дроби сократятся с знаменателем наименьшего коэффициента, обводимся от них.

Заметим, что каждый элемент имеет при себе b. Сокращаем всё на b.
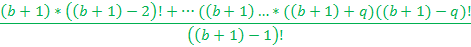
Далее определяем делимость каждого элемента на второй коэффициент.
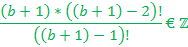
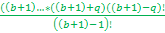

Формула максимального значения уникального коэффициента, сокращённого на P(п)
 =
= 
Зная всё выше перечисленное, выведем общую формулу простого числа
формула простого числа
 (
(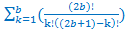 ) = P
) = P
b = (2N+1) + (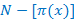 )
)
Однако за не имением, на данный момент, точной формулы дающей истинную оценку количества простых чисел  припишем формулу, опираясь на данные, доступные на данный момент, что значительно снизит достоверность данного алгоритма.
припишем формулу, опираясь на данные, доступные на данный момент, что значительно снизит достоверность данного алгоритма.
«Формальная» формула простого числа
 (
(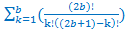 ) = Pф
) = Pф
b = N + Фс+ Фп
Фс ~  ; Фп
; Фп 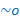
Где N – порядковый номер простого числа, Фс – количество чисел не удовлетворяющих малой теореме Ферма, на интервале от 1 до N. 3-отношения количества всех чисел,(на интервале от 1 до N) к количеству чисел вида
 . Фп - количество псевдо-простых чисел, удовлетворяющих МТФ. []-округление вверх.
. Фп - количество псевдо-простых чисел, удовлетворяющих МТФ. []-округление вверх.
Выявим фактор простоты числа Фс
Для этого из количества чисел, проходящих проверку Фактора простоты, вычтем те, что её заведомо не пройдут.
Фс ~ 
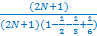 = 3
= 3
Найдем во сколько раз уменьшиться количество, потенциально составных чисел, при исключении чисел кратных 2 и 3. Поскольку в множестве потенциально простых, отсутствуют числа кратные 2 и 3. Для этого разделим общее количество простых чисел, на количество оставшихся чисел, после исключения 2 и 3. Количество оставшихся чисел, после исключения 2 и 3, определим вычтя из общего количества, числа кратные 2 и 3. Поскольку, вычитая числа кратные 2, мы уже вычли некоторые числа, которые пересекаются с числами кратными 3, т.е. числа кратные 6, вычитались дважды, возвращаем их.
Выявим фактор псевдо-простоты числа Фп
d – порядковый номер числа
| N | Pп=b+1 | Уровень проверки | 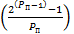 = = 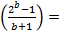 
| b= |
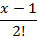
| 
| 2d | ||
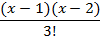
| 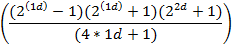
| 4d | ||
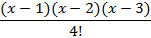
| 
| 6d | ||
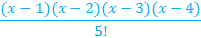
| 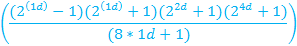
| 8d | ||
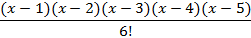
| 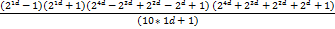
| 10d | ||

| 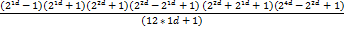
| 12d | ||
| 340d |
P(п)= 3

 =
=  -1=0
-1=0
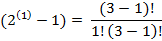
P(п)=5
 -
-  =
=  =0
=0
P(п)=7
 -
- 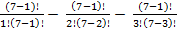 =
= 
P(п)=9
 =
= 
P(п)=11
 -
- 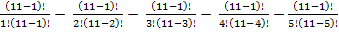 =
= 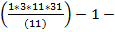 5 -15 -30-42=0
5 -15 -30-42=0
P(п)=13
(21-1)(21+1)(22+1)(22-2+1) (22+2+1)(24-22+1) - 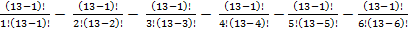 =
=
 1-6-22-55-99-132=0
1-6-22-55-99-132=0
Вывод: все поставленные задачи были решены в ходе данной работы.
Примечание:
Фс – точность вычисления, количества чисел не удовлетворяющих малой теореме Ферма, на интервале от 1 до N, может быть повышена до абсолютной.
Вычисление Pф – может быть существенно облегчено, путём взаимного сокращения, частного и делителя
Список литературы и интернет источников:
https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D1%81%D1%82_%D0%90%D0%B3%D1%80%D0%B0%D0%B2%D0%B0%D0%BB%D0%B0_%E2%80%94_%D0%9A%D0%B0%D1%8F%D0%BB%D0%B0_%E2%80%94_%D0%A1%D0%B0%D0%BA%D1%81%D0%B5%D0%BD%D1%8B
https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0
https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D0%BB%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A4%D0%B5%D1%80%D0%BC%D0%B0