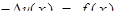
 (1)
(1)

 (2)
(2)
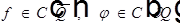 - это не гарантирует существование решения.
- это не гарантирует существование решения. 
Теорема.
Задача (1) (2) может иметь не более одного классического решения.
Доказательство.
Предположим противное: пусть есть два классических решения: 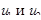 . Это значит:
. Это значит:

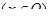 (3)
(3)
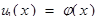
 (4)
(4)

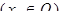 (5)
(5)

 (6)
(6)

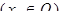 (7)
(7)
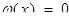
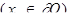 (8)
(8)
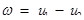
Значит: 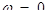 и
и 
Следовательно, если существуют два решения, то они равны друг другу. Что и требовалось доказать.
Обобщенные решения смешаной задачи для волнового уравнения.
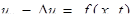
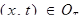 (1)
(1)
 (2)
(2)

 (3)
(3)

 (4)
(4)
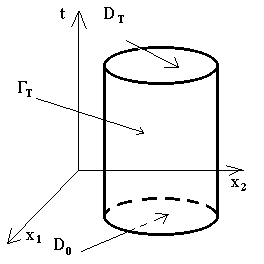


Обозначения: 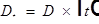 ;
; 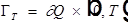 .
.
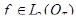



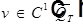 :
: 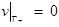 ,
, 
Умножим обе части на v и проинтегрируем по цилиндру:

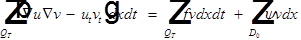 (5)
(5)
Хотя обобщенное решение - общее понятие, но классическое решение
может не быть обобщенным.
Определение.
Обобщенное решение - функция u из 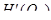 - называется
- называется
обобщенным решением задачи (1)-(4), если 
 и для
и для
 , такого, что
, такого, что  и
и 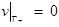 выполняется интегральное
выполняется интегральное
тождество (5).
Существование обобщенного решения первой смешанной задачи для волнового уравнения.
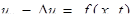
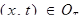 (1)
(1)
 (2)
(2)

 (3)
(3)

 (4)
(4)
 ,
, 


 (6)
(6)
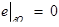 (7)
(7)
 - ограниченная область;
- ограниченная область; 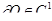

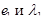 ,
,  ,...,
,..., 
 - базис,
- базис,
тогда: 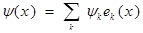

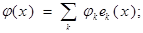 где:
где: 

По теореме Фубини:

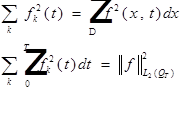
 (8)
(8)
Теорема.
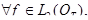

 ряд (8) сходится в пространстве
ряд (8) сходится в пространстве 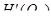 и сумма этого ряда является обобщенным решением задачи (1)-(4). При этом имеет место оценка:
и сумма этого ряда является обобщенным решением задачи (1)-(4). При этом имеет место оценка: 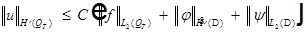 (9)
(9)
Доказательство.
Первый этап.
Пусть: 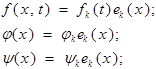
Докажем, что тогда решение u(x,t) имеет вид:

 (10)
(10)
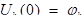 (11)
(11)
 (12)
(12)
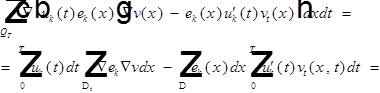
при почти всех t  .
.
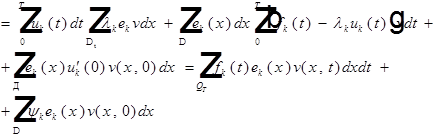
Доказано:
если 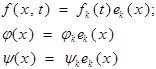 , то:
, то:  - решение.
- решение.
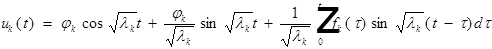
Второй этап.
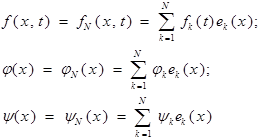
то: 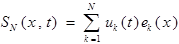 -обобщенное решение смешанной задачи.
-обобщенное решение смешанной задачи.
Третий этап.
Докажем, что решения смешанной задачи со специальной правой частью сходятся к обобщенному решению.
Осуществляется предельный переход:
Оценим  и их производные:
и их производные:
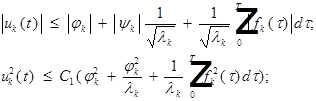

Докажем, что последовательность фундаментальна.
Пусть N>M; рассмотрим:

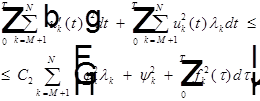

Значит 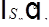 -фундаментальная в
-фундаментальная в  - полном, т.е.
- полном, т.е.  .
.

Надо доказать, что u - обобщенное решение, если 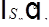 -обобщенное решение.
-обобщенное решение.

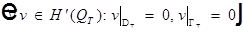 ; при переходе к пределу получим:
; при переходе к пределу получим:

Единственность обобщенного решения первой смешанной задачи для волнового уравнения.

 (1)
(1)
 (2)
(2)

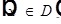 (3)
(3)
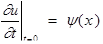
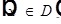 (4)
(4)
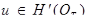



Теорема 1.
Задача (1) - (4) может иметь не более одного обобщённого решения.
Доказательство.
Достаточно убедится, что однородная задача будет иметь единственное решение.

Возьмем:

где: 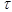 - произвольная,
- произвольная,  .
.
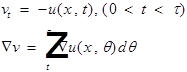
Интегральное тождество приобретет следующий вид:

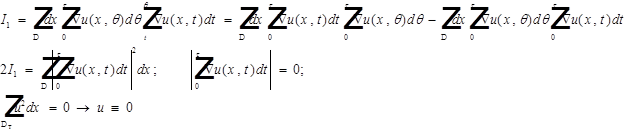 Теорема доказана.
Теорема доказана.
Анизотропные пространства Соболева.
Определение.
Анизотропным пространством Соболева  называется множество функций
называется множество функций  .
.
Вводится скалярное произведение:  (1)
(1)
Свойства пространств:
Теорема.
Пространство  -полно.
-полно.
Доказательство.
Фундаментальная последовательность, переход к пределу в интегральном тождестве.
Пусть 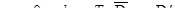 через
через  .
.
Теорема 2.
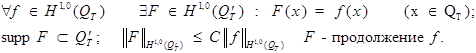
Теорема 3.
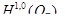 -сепарабельно.
-сепарабельно.
Доказательство - продолжение функции до финитной.
Теорема 4.

 всюду плотно в
всюду плотно в  . Возьмем
. Возьмем 

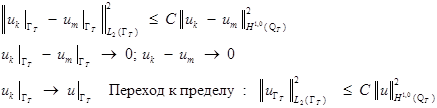
Теорема 5.
Для  можно определить след:
можно определить след: 
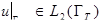 и при этом:
и при этом: 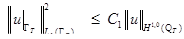 .
.
Обобщенные решения смешанной задачи для
уравнения теплопроводности.
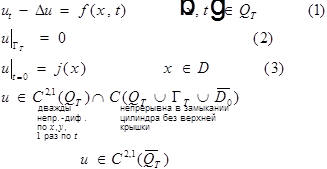

Определение.
Обобщенное решение  - называется обобщенным решением задачи (1)-(3), если
- называется обобщенным решением задачи (1)-(3), если  :
:  выполняется интегральное тождество (4).
выполняется интегральное тождество (4).
Существование обобщенного решения первой смешанной задачи для уравнения теплопроводности (метод Фурье, метод разделения переменных).

 - собственные значения;
- собственные значения;
 - ортогональный базис в
- ортогональный базис в  ;
;
 - ортонормированный базис в
- ортонормированный базис в  .
.
Будем считать: 

при почти всех t интегрируема с квадратом в  .
.
Равенство Парсеваля:
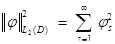 f -измерима и
f -измерима и 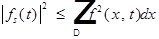 по неравенству Гельдера.
по неравенству Гельдера.  .
.
По теореме Лебега можно слева и справа проинтегрировать по t и поменять местами 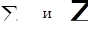 .
.
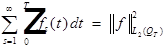
Решение имеет вид:

Надо доказать сходимость в  .
.
Теорема.
 ряд (6) сходится в пространстве
ряд (6) сходится в пространстве  к некоторой функции
к некоторой функции  , которая является обобщенным решением задачи (1)-(3). При этом:
, которая является обобщенным решением задачи (1)-(3). При этом:

Доказательство.
Первый этап.
Предположим, что правая часть уравнения имеет вид: 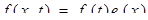 , а начальная функция:
, а начальная функция:  .
.
Рассмотрим:

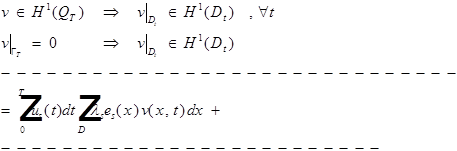
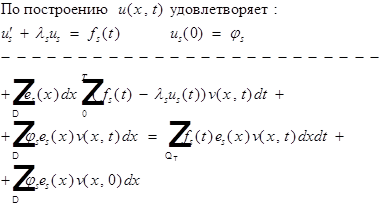
-интегральное тождество выполняется.
Второй этап.
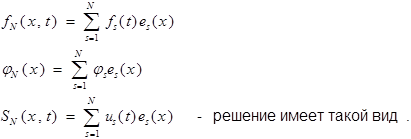
Третий этап. Доказательство фундаментальности последовательности 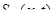 . Оценим модуль:
. Оценим модуль:
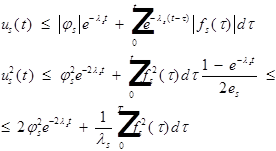
Интегрируем слева и справа:


Значит: последовательность фундаментальна и она сходится:
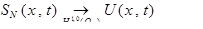
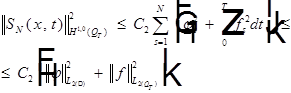
Переходим к пределу:

Надо доказать, что u - задает решение задачи.
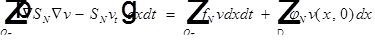
При переходе к пределу выполняется интегральное тождество:

Теореме доказана. Из этой теоремы не следует единственность.
Единственность обобщенного решения смешанной задачи для уравнения теплопроводности.
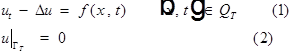
Теорема.
Задача (1)-(3) может иметь не более одного обобщенного решения.
Доказательство.
Пусть  -обобщенные решения, оценим
-обобщенные решения, оценим  .
.

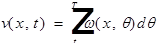 - добавлена гладкость по t.
- добавлена гладкость по t.
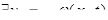
Условия, налагаемые на v: 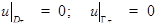 .
.

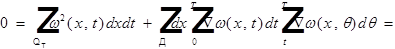
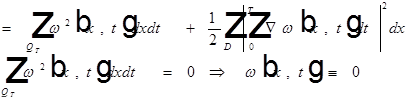
Формула Кирхгофа.
Дополнительные обозначения:
пусть есть  ,
,  - фиксируется. Обозначим:
- фиксируется. Обозначим:  - конус с вершиной в
- конус с вершиной в  .
.
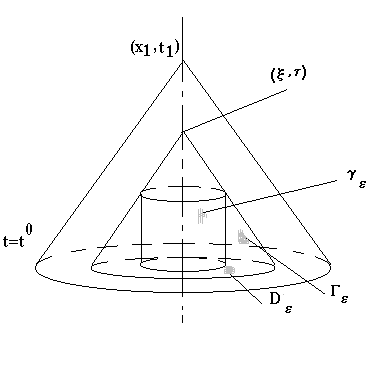
Возьмем произвольную 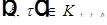 .
.
Обозначим:
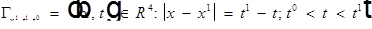
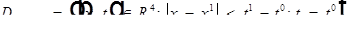 .
.
Выберем  и рассмотрим:
и рассмотрим:  - вне цилиндра, но внутри конуса.
- вне цилиндра, но внутри конуса.
Обозначим через 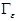 - часть конической поверхности, ограниченной
- часть конической поверхности, ограниченной  :
: 
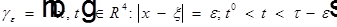

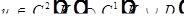 - дважды непрерывно дифференцируема в открытом конусе. При этом:
- дважды непрерывно дифференцируема в открытом конусе. При этом:  - замыкание конуса.
- замыкание конуса.
Замечание:  - волновой оператор.
- волновой оператор.
Рассмотрим вспомогательную функцию: 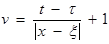 .
.
Рассмотрим: 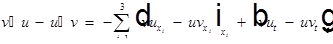 . Заметим:
. Заметим: 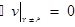 .
.
В дальнейшем: x принадлежит малому конусу с вырезанным цилиндром.
Проинтегрируем левую и правую части тождества по 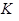 :
:
 ,
,
где: - единичный вектор внешней нормали к границе области.
Разобьем этот интеграл на 3 интеграла: 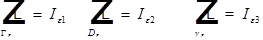 ;
;
потом  .
.
Рассмотрим на конической поверхности 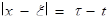 интеграл
интеграл 
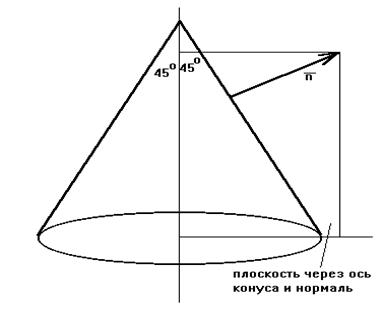
Вычислим все частные производные функции v по 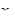 и по направлению внешней нормали к поверхности:
и по направлению внешней нормали к поверхности: 

Зная, что 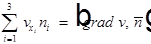 , получим:
, получим: 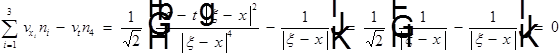 ,
,
где: 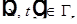 . Вывод:
. Вывод: 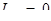 .
.
Рассмотрим 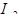 , зная, что для
, зная, что для  .
.

Переход к пределу:

Вычислим: 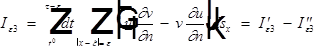
 - внутренняя нормаль к цилиндру.
- внутренняя нормаль к цилиндру.
Т.к. u - непрерывно дифференцируема на поверхности, то:


учитывая: 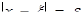 на цилиндрической поверхности.
на цилиндрической поверхности.

В силу оценки: 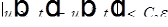
Получим: 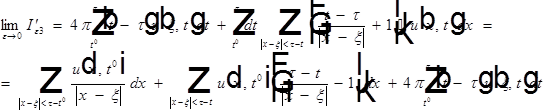

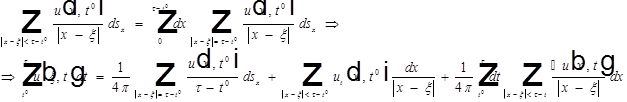




Получена формула Кирхгофа: (1)

|
Замена переменных (чтобы легче было дифференцировать по t):

 Продифференцировано первое слагаемое:
Продифференцировано первое слагаемое: 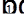

Геометрический смысл формулы.
1. В первых двух интегралах производится интегрирование по границе основания конуса - трехмерной сфере.
2. В третьем интеграле производится интегрирование по основанию конуса - трехмерному шару.
3. Значение даламбериана вычисляется интегрированием по боковой поверхности конуса.
СМЫСЛ. Дважды дифференцируемая функция u(x,t) выражается через значение первых производных на сфере (границе основания конуса) и её даламбериан на боковой поверхности конуса.
Задача Коши для волнового уравнения.
Обозначим: 
Определение.
Функция u(x,t), такая, что:
1)  - дважды непрерывно дифференцируемая на
- дважды непрерывно дифференцируемая на  ;
;
2) 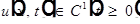 - один раз непрерывно дифференцируемая в замыкании этого множества;
- один раз непрерывно дифференцируемая в замыкании этого множества;
называется классическим решением задачи Коши для волнового уравнения, если:
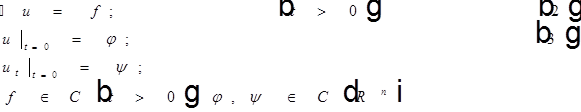
Пусть n=3.
Обозначим: 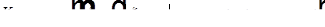
По формуле Кирхгофа функция u(x,t) выражается для любого конуса  через функции
через функции  в этом конусе. Функция u(x,t) однозначно определяется функциями
в этом конусе. Функция u(x,t) однозначно определяется функциями  в любом конусе и, значит, в полупространстве.
в любом конусе и, значит, в полупространстве.
Теорема единственности.
Задача Коши (2)-(3) не может иметь более одного решения.
Вопрос существования.
Если классическое решение существует, то оно задается формулой Кирхгофа (4):

Таким образом, вопрос о существовании классического решения
сводится к нахождению условий, налагаемых на функции  , при которых функция, стоящая в правой части формулы (4), является решением этой задачи. Получено лишь достаточное условие.
, при которых функция, стоящая в правой части формулы (4), является решением этой задачи. Получено лишь достаточное условие.
Предварительные рассуждения.
Введем функцию: 
Есть  . Для каждого
. Для каждого  определяется
определяется 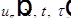 как интеграл.
как интеграл.
Производится исследование 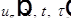 .
.
Лемма 1.
Пусть функция g и все её производные по пространственным переменным непрерывны до порядка k:  , тогда:
, тогда:
1) функция и все её производные вплоть до порядка k по x и t непрерывны на множестве  :
: 
2) для 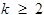 и
и 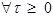 функция
функция  удовлетворяет однородному волновому уравнению при и следующим условиям:
удовлетворяет однородному волновому уравнению при и следующим условиям: 
Доказательство.
В (5) перейдем к новой переменной, тогда: 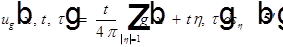
Отсюда следует первое утверждение леммы.
Применим 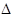 к
к  , тогда:
, тогда: 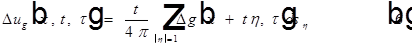
Подставим t=0:  .
.
Возьмем производные по t от  :
:  .
.
Рассмотрим производную при t=0: 
Преобразуем второе слагаемое: 
обозначим: 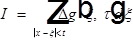
тогда (7) примет вид:  .
.
Используем его для вычисления второй производной по времени: 

Предствляя этот объемный интеграл в виде повторного интеграла: сначала по сфере, а затем от 0 до t, получим равенство:  - вследствие формулы (6) справедливо последнее равенство.
- вследствие формулы (6) справедливо последнее равенство.
Лемма доказана.
Теорема 2.
Пусть:
 - трижды непрерывно дифференцируемая в
- трижды непрерывно дифференцируемая в 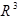 :
: 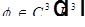 ;
;
 - дважды непрерывно дифференцируема в
- дважды непрерывно дифференцируема в 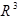 :
: 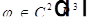 ;
;
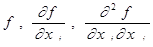 - непрерывны:
- непрерывны:  ;
;
тогда: решение задачи Коши (2)-(3) существует и дается формулой Кирхгофа (4).
Доказательство.
Рассмотрим второе слагаемое:  в силу леммы 1 есть:
в силу леммы 1 есть: 
Рассмотрим первое слагаемое 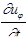 . T.к.
. T.к. 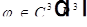 , то:
, то: 
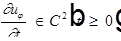
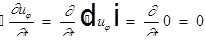
Начальные условия:  ;
;  .
.
Рассмотрим: 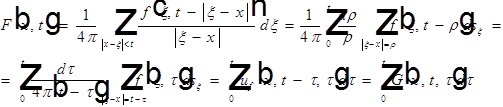 ,
,
где:  - обозначение.
- обозначение.
В силу леммы 1 G и все её производные по x и t до второго порядка включительно непрерывны на множестве  .
.
Функция G удовлетворяет: 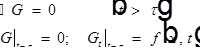
Перейдем к F. F непрерывна вместе со всеми производными по x до второго порядка включительно в области  , и её первая производная по времени непрерывна в этой области.
, и её первая производная по времени непрерывна в этой области.
Вычислим производную F по t: 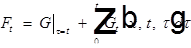 но:
но:  , и:
, и:  Следует:
Следует:  .
.
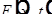 - удовлетворяет волновому уравнению:
- удовлетворяет волновому уравнению: 
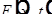 - удовлетворяет однородным начальным условиям:
- удовлетворяет однородным начальным условиям: 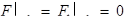
Окончательно:  - удовлетворяет волновому уравнению
- удовлетворяет волновому уравнению  и начальным условиям:
и начальным условиям:  .
.
Замечание.
Доказательство теоремы о существовании и единственности классического решения задачи Коши в случае, когда n=3, опиралось на интегральное представление функции в виде формулы Кирхгофа. Формулы, аналогичные формуле Кирхгофа, можно вывести для произвольного числа пространственных переменных. Эти формулы дают выражение достаточно гладкой функции u(x,t) через её первые производные и даламбериан в конусе.
Пользуясь этим представлением, можно обобщить эти теоремы существования и единственности для произвольного числа переменных (n>3).
Замечание.
Формулы, аналогичные формулам Кирхгофа для n=1 и n=2, можно получить из n=3 методом спуска.
Метод спуска (как из формулы Кирхгофа получить формулы Пуассона и Даламбера).
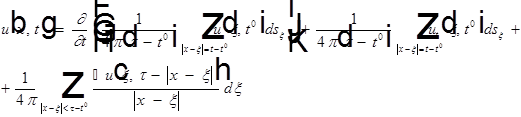
Надо получить формулу Кирхгофа для n=2 - формулу Пуассона.
Обозначения: 
Преобразуем интегралы:

 Рассмотрим:
Рассмотрим: 
Заменим 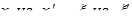 .
.
Получим формулу:
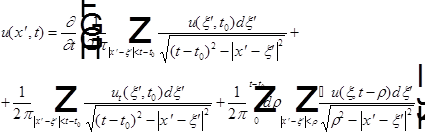
Получена формула Пуассона:
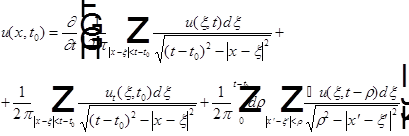
Формула Даламбера:
Обозначим:  .
.
Введём фундаментальное решение уравнения теплопроводности:
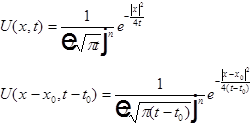
Свойства U для уравнения теплопроводности.
1. 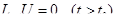
2.Если U продолжить тождественным 0 при  , то такая функция
, то такая функция 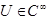 - бесконечно дифференцируема.
- бесконечно дифференцируема.
Доказательство.
Если выписывать производные функции U, то получится рациональная функция, умноженная на экспоненту, экспонента стремится к 0 быстрее любой рациональной функции, значит, пределы все равны 0, и получена бесконечная гладкость.
3. 
Доказательство.
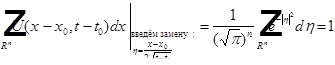
В качестве упражнения:  .
.
4. 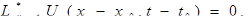
где 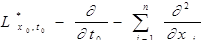 - формула представления решения задачи Коши для уравнения теплопроводности.
- формула представления решения задачи Коши для уравнения теплопроводности.
Дополнительные обозначения.
Пусть 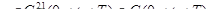 , пусть u, Lu - ограничены в полосе.
, пусть u, Lu - ограничены в полосе.
Введём  , обладающую свойством:
, обладающую свойством: 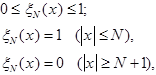
 - используются срезающие функции.
- используются срезающие функции.

n - размерность постранства 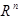 .
.
N - определяет область интегрирования.
Будем считать:
 - интегрирование по цилиндру.
- интегрирование по цилиндру.
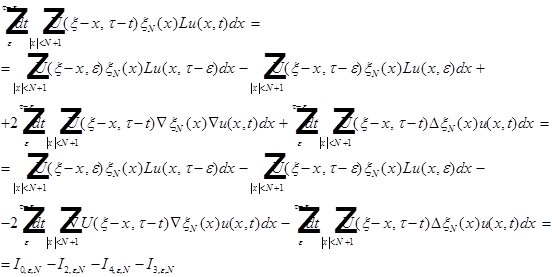
Сначала рассмотрим интеграл:

Можно применить теорему Лебега о предельном переходе под знаком интеграла:
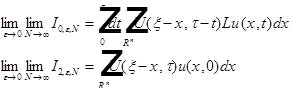
Т.к.  , то
, то

произведём замену 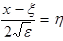 , тогда
, тогда 

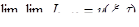 .
.
Если докажем, что остальные пределы дают 0.
Формула Пуассона:
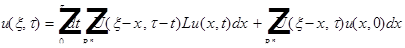

Можно найти решение задачи Коши для уравнения теплопроводности:
Рассматривается задача:
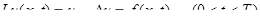 (1)
(1)
 (2)
(2)
Если решение из рассматриваемого класса существует, то оно представляется формулой:  .
.
В рассматриваемом классе решений задача Коши для уравнения теплопроводности может иметь не более 1 решения.



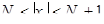
Применим теорему Лебега о предельном переходе под знаком интеграла
(необходимо, чтобы все элементы последовательности были ограничены интегральной функцией).

где:  .
.
Подынтегральная функция ограничена.
Так как: 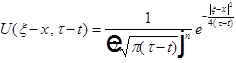 , то:
, то:
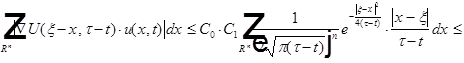
Замена:  .
.
 , а интеграл
, а интеграл  - сходящийся.
- сходящийся.
Сделано ограничение интегрируемой функцией.
Можно применять теорему Лебега о предельном переходе.
Теория Фредгольма.
(в Гильбертовом или Банаховом пространстве).
Рассмотрим компактный оператор 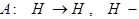 гильбертово пространство.
гильбертово пространство.
Изучаем уравнение:
 (1)
(1)
однородное уравнение 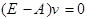 (2)
(2)
однородное сопряженное уравнение 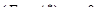 (3)
(3)
Теорема Фредгольма.
Теорема.
1. Если однородное уравнение (2) имеет единственное тривиальное решение, то неоднородное уравнение (1) имеет единственное решение для любой правой части из гильбертова пространства H.
2. Если уравнение (2) имеет нетривиальное решение, то тогда неоднородное уравнение (1) разрешимо тогда и только тогда, когда правая часть уравнения (1) ортогональна всем решениям уравнения (3):  .
.
3. Размерность ядра оператора  равна размерности оператора
равна размерности оператора  и конечна.
и конечна.
 .
.
Введём: 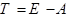 , тогда
, тогда  .
.
Лемма 1.
 ,
,  .
.
Доказательство.
Предположим противное: 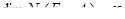 .
.
Ядро - замыкает линейное подпространство.
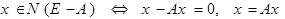
Следовательно единичный шар отображается на себя (в некомпактное множество), а оператор компактный.
Ядро - замыкание бесконечномерного подпространства Гильбертова пространства.
Имеем противоречие, доказывающее теорему.
Лемма 2.
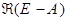 ,
, 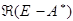 - замкнуты в подпространстве.
- замкнуты в подпространстве.
Доказательство.
Пусть  . Докажем, что
. Докажем, что  .
.
 .
.
Разложим  на ортогональные составляющие.
на ортогональные составляющие.

 , где
, где 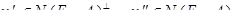 .
.
Значит: 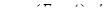 .
.
1).  - ограниченная последовательность, следовательно можно выбрать подпоследовательность
- ограниченная последовательность, следовательно можно выбрать подпоследовательность  такую, что
такую, что  - сходящаяся.
- сходящаяся.
Тогда: 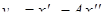 . В этом случае
. В этом случае 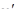 сходится в H.
сходится в H.
 .
.
2).  - неограниченная. Можно выбрать подпоследовательность
- неограниченная. Можно выбрать подпоследовательность 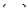 такую, что:
такую, что:
 , тогда:
, тогда:
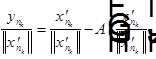 ,
, 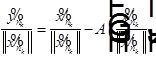 .
.
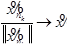 ,
,  ,
, 
Из сходимости следует, что ненулевые элементы принадлежат ядру и ортогональному дополнению:  .
.
Лемма 3.
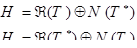
Доказательство. (первая часть)
Пусть  , тогда:
, тогда: 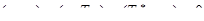 .
.
Получили:  .
.
Пусть 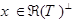 , тогда:
, тогда:  .
.
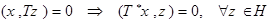 .
.
Значит:  .
.
Введём обозначения:

Лемма 4.
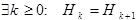 .
.
Доказательство.
Предположим противное: пусть такого k не существует.
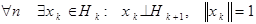 .
.
Возьмём n<m и рассмотрим 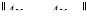 .
.
При этом  .
.
 .
.
Из подпоследовательности  нельзя выбрать фундаментальную подпоследовательность:
нельзя выбрать фундаментальную подпоследовательность:  - фундаментальна.
- фундаментальна.
Получили противоречие.
Лемма 5.
Пусть