Содержание
Задание 1. 3
Задание 2. 5
Задание 3. 8
Задание 4. 10
Задание 5. 14
Задание 6. 18
Задание 7. 21
Задание 1.
Найти реакции связей (опор), наложенных на основное тело конструкции – балку или сварной стержень.

Рисунок 1.1
Дано: G = 6 кН; Р = 7 кН; М = 4 кНм; q = 3 кН/м; α = 60°
Решение:
1. Рассмотрим равновесие балки в пространстве Аху основания (искомые силы приложены к ней, рис. 1.2).
2. Заданные силы, приложенные к балке: Q – равнодействующая распределенных сил постоянной интенсивности (Q = q∙2 = 6 кН,приложена в точке А), сила тяжести G, силаР, направленная под углом α,и пара сил с моментом М.
3. Связи: невесомый стержень ВD (связь первого вида) и неподвижный шарнир А (связь второго вида). Заменим связи реакциями.
Направление реакции 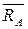 неизвестно, поэтому покажем ее двумя составляющими
неизвестно, поэтому покажем ее двумя составляющими  и
и 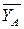 . Реакция
. Реакция 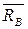 направлена вдоль стержня.
направлена вдоль стержня.

Рисунок 1.2
4. Выпишем уравновешенную на теле систему сил (заданных и реакций связей).
Составим три уравнения равновесия сил в координатной форме.
Получим:

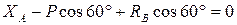 (1)
(1)
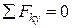
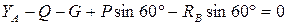 (2)
(2)

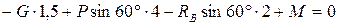 (3)
(3)
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.
Из уравнения (3) выразим RВ
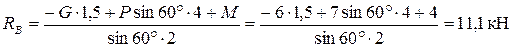
Из уравнения (2) выразим YА
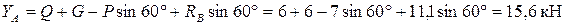
Из уравнения (1) выразим ХB
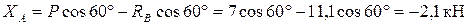
Значение ХА оказалось отрицательным. Это означает, что действительное направление этой силы противоположно показанному на рис. 1.2.
Реакция  неподвижного шарнира может быть построена по составляющим
неподвижного шарнира может быть построена по составляющим  ,
, 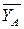 , а ее модуль равен:
, а ее модуль равен:
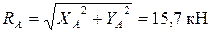
Ответ: 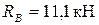 ;
; 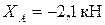 ;
; 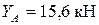 ;
; 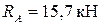
Задание 2.
По заданным уравнениям движения точки М в декартовых координатах x = f1(t), y = f2(t) найти:
1) уравнение траектории движения точки;
2) скорость и ускорение точки в произвольный момент времени t, а также в момент времени t = t1;
3) касательное и нормальное ускорения точки в момент времени t1;
4) радиус кривизны траектории в точке, совпадающей с положением точки М в момент времени t = t1.
Кроме того, построить, выбрав соответствующие масштабы для
длин, скоростей и ускорений:
1) траекторию точки;
2) положение точки на траектории в момент временя t = t1;
3) скорость и ускорение точки, а также касательное и нормальное ускорения для момента времени t = t1.
Дано:  , см;
, см; 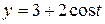 , см; t1 = π/3 с.
, см; t1 = π/3 с.
Решение:
Для определения уравнения траектории точки исключим из заданных уравнений движения время 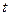 .
.
Из уравнения  выразим величину
выразим величину 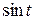 :
:

Из уравнения 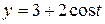 выразим величину
выразим величину 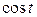 :
:
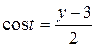
Воспользуемся формулами тригонометрии:

Получим
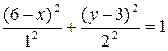 - уравнение эллипса (рис. 2.1).
- уравнение эллипса (рис. 2.1).
Найдем положение точки М при t1 = π/3 с:
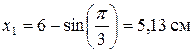 ;
; 
Изобразим точку М на траектории движения (рис. 2.1)
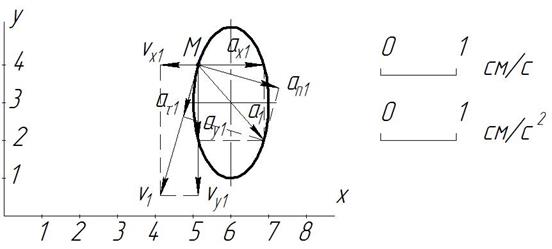
Рисунок 3.1
Скорость точки найдем по ее проекциям на оси координат:
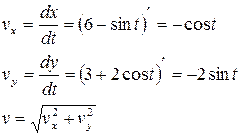
при t1 = π/3 c имеем
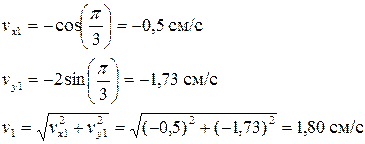
Аналогично найдем ускорение точки
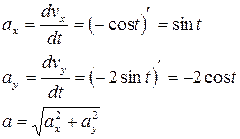
при t1 = π/3 c имеем
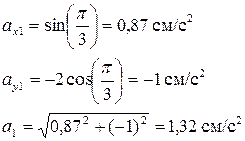
Касательное ускорение найдем, дифференцируя по времени равенство 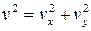 . Получим:
. Получим:
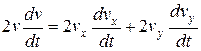
откуда
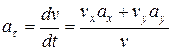
при t1 = π/3 c имеем
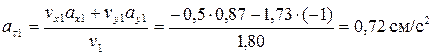
Нормальное ускорение точки

при t1 = π/3 c имеем
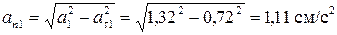
Радиус кривизны траектории
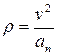
при t1 = π/3 c имеем
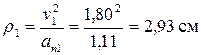
Построим векторы скорости и ускорения для соответствующей точки М на ее траектории.
Ответ: 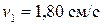 ;
;  ;
; 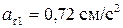 ;
; 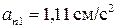 ;
; 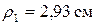
Задание 3.
По заданному уравнению прямолинейного поступательного движения груза 1 определить скорость, а также касательное, нормальное и полное ускорения точки М механизма в момент времени t1, когда путь, пройденный грузом, равен S.
Показать на рисунке векторы скорости и ускорения точки.
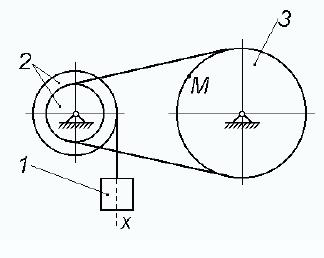
Рисунок 3.1
Дано: R2 = 15 см, r2 = 10 см, R3 = 20 см;  , см; S = 0,2 м = 20 см.
, см; S = 0,2 м = 20 см.
Решение:
Уравнение движения груза 1 имеет вид:

Так как за время от t0 = 0 до t1 (груз пройдет расстояние S = x1-х0, то формула
для определения пути S будет иметь вид:
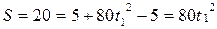
или
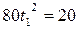
Решая это квадратное уравнение, находим, что t1 = 0,5 с.
Скорость груза 1
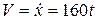
пpи t= t1 = 0,5 c 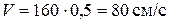
Ускорение груза 1
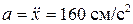
2. Угловая скорость ступенчатого колеса 2
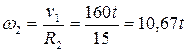
Колесо 2 вращается по часовой стрелке.
3. Угловая скорость колеса 3. Угловые скорости двух колес, связанных ременной передачей, обратно пропорциональны их радиусам:
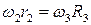
откуда угловая скорость колеса 3:

Колесо 3 вращается по часовой стрелке
4.Угловое ускорение колеса 3
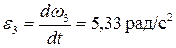
Направление углового ускорения совпадает с направлением вращения колеса, следовательно колесо 3 вращается ускоренно
5. Скорость точки М
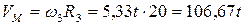
При t1 = 0,5 c: 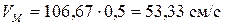
6.Нормальное ускорение точки М:

При t1 = 0,5 c: 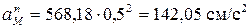
8. Тангенциальное ускорение точки М

9.Полное ускорение точки М
Скорости и ускорения тела 1 и точки М показаны на рис. 3.2.
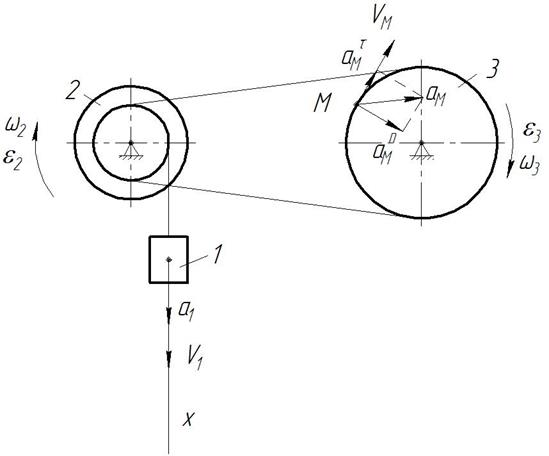
Рисунок 3.2.
Ответ:  ;
; 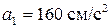 ;
; 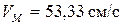 ;
; 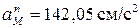 ;
;  ;
; 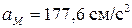 .
.
Задание 4.
Найти для заданного положения механизма скорости и ускорения точек В к С, а также угловые скорость и ускорение звена, которому эти точки принадлежат. Схема механизма приведена на рисунке 4.1.
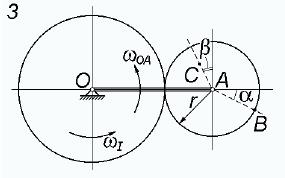
Рисунок 4.1
Дано: 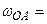 3 рад/с;
3 рад/с; 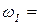 8 рад/с; r = 18 см; ОА = 48 см, АС = 3 см; α = 135°; β = 90°.
8 рад/с; r = 18 см; ОА = 48 см, АС = 3 см; α = 135°; β = 90°.
Решение:
Скорость точки А
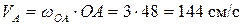
Скорость точки К

Определим положение мгновенного центра скоростей колеса II (точка Р2):
пусть  , тогда
, тогда 
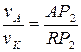 или
или 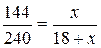
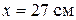 ;
;  .
.
Угловая скорость колеса II
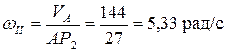
Определим расстояния от точек С и В до мгновенного центра скоростей:
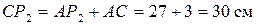
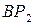 определим из треугольника АВР2 по теореме косинусов:
определим из треугольника АВР2 по теореме косинусов:
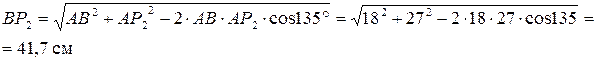
Скорость точки В

направлена перпендикулярно 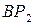 в направлении
в направлении  .
.
Скорость точки С
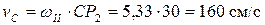
направлена перпендикулярно 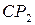 в направлении
в направлении  .
.
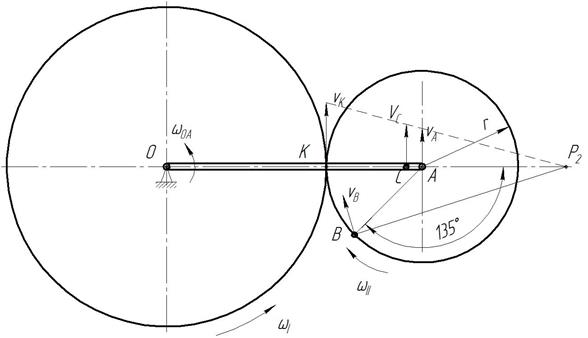
Рисунок 4.2
Ускорение точки А
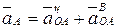
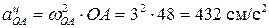 - центростремительное
- центростремительное
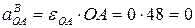 - вращательное ускорение
- вращательное ускорение
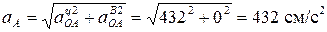
Угловое ускорение колеса II

Ускорение точки В
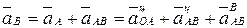
где  - направлено от В к А.
- направлено от В к А.
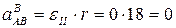
найдем проекции на оси х и y

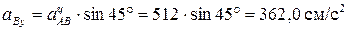
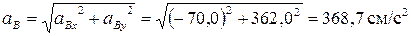
Ускорение точки С
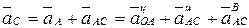
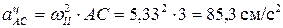

найдем проекции на оси х и y
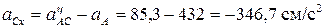

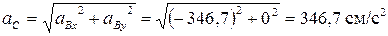
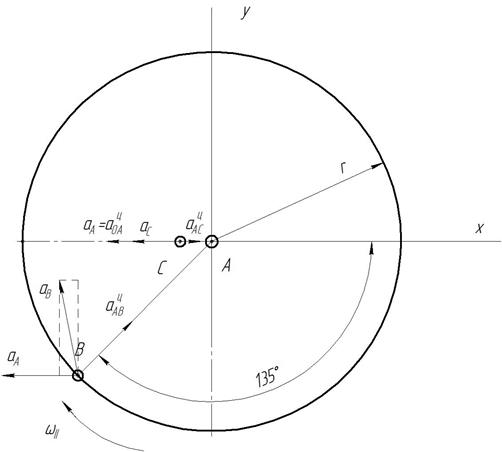
Рисунок 4.3
Ответ: 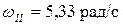 ,
,  ,
, 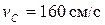 ;
;  ;
; 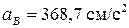 ,
, 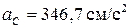
Задание 5.
Тело движется из точки А но участку АВ (длиной 1), наклонному или горизонтальному в течение τ с. Его начальная скорость vА. Коэффициент трения скольженяя тела по плоскости равен f. В точке В тело покидает плоскость со скоростью vBи попадает в точку Ссо скоростью vCнаходясь в воздухе в течение T секунд.
При решений задачи тело принять за материальную точку; сопротивление воздуха не учитывать.
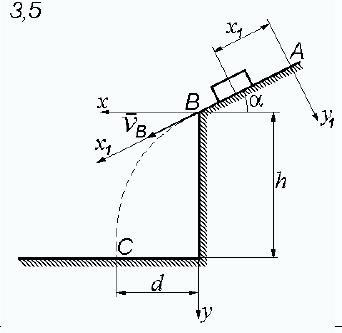
Рисунок 5.1.
Дано: α = 30º; f =0,1; vA = 1 м/с; τ = 1,5 с; h = 10 м.
Найти: vB -? d -?
Решение:
Рассмотрим движение тела на участке АВ. Принимая тело за материальную точку, показываем на рисунке 4 действующие на него силы: вес G, нормальную реакцию N и силу трения скольжения F. составляем дифференциальное уравнение движения
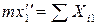 ;
; 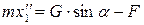
Сила трения 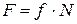
где 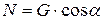 - нормальная реакция
- нормальная реакция
Таким образом
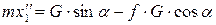
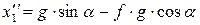
Интегрируя дифференциальное уравнение дважды получаем
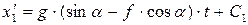
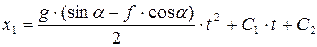

Рисунок 5.2.
Для определения постоянных интегрирования используем начальные условия задачи:
при t = 0 с х1 = 0 
Подставляя t = 0 в уравнения, полученные при интегрировании, имеем:
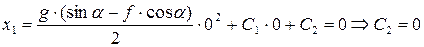

Тогда имеем уравнения движения тела на участке АВ
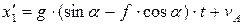
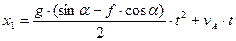
Для момента времени τ, когда тело покидает наклонный участок 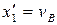
т.е
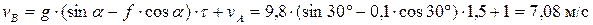
Далее рассматриваем движение тела от точки В до С.
Покажем силу G, действующую на тело. Составим дифференциальные уравнения его движения по осям х и y:
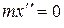 ;
; 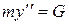
Интегрируя 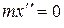 имеем:
имеем:
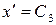
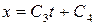
Определяем постоянные С3 и С4 используя начальные условия:
при t = 0 с х = 0 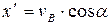
Подставляя t = 0 в уравнения, полученные при интегрировании, имеем:
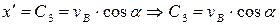
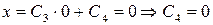
Тогда

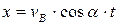
Интегрируя 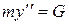 имеем:
имеем:
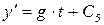
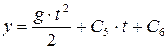
Определяем постоянные С5 и С6 используя начальные условия:
при t = 0 с y = 0 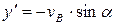
Подставляя t = 0 в уравнения, полученные при интегрировании, имеем:
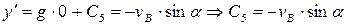

Тогда
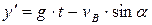
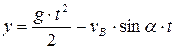
Уравнение траектории тела на участке ВС находим исключая параметр t
Из уравнения 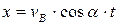 имеем
имеем  . Подставляя полученное значение в уравнение
. Подставляя полученное значение в уравнение 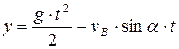 имеем
имеем
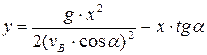
В момент падения камня y = h = 10 м, 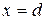 , отсюда
, отсюда
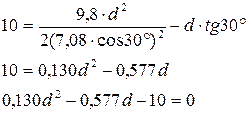
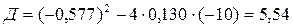
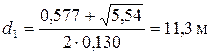
 – не подходит, так как расстояние не может быть отрицательной величиной.
– не подходит, так как расстояние не может быть отрицательной величиной.
Получили 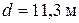
Ответ:  с;
с; 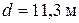
Задание 6.
Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рис. 6.1. Учитывая трение скольжения тела 1, пренебрегая массами нитей и предполагая их нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным S.

Рисунок 6.1
Дано: m1 =m кг; m2 =m кг; m3 =0,1m кг; m4 = 0,2m кг; α = 30°; f = 0,10; S = 1 м;
Найти: V1 -?
Решение:
1. Скорости и перемещения тел
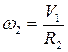


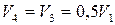
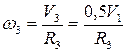
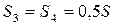
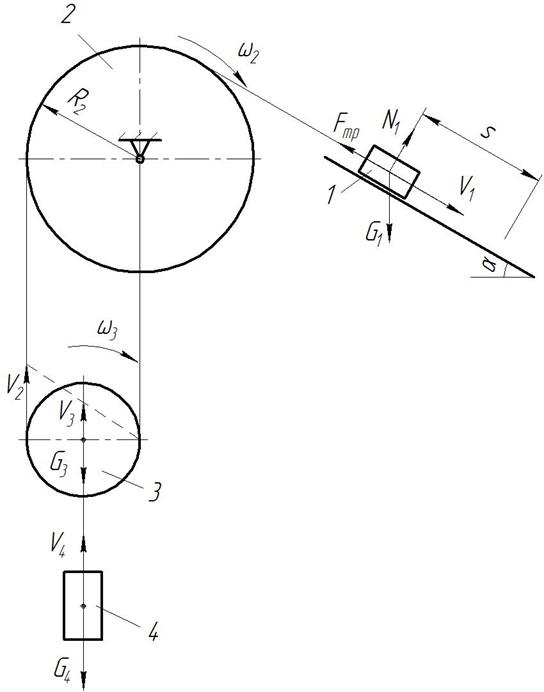
Рисунок 6.2
2. Кинетическая энергия тел.
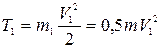
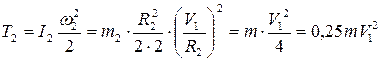
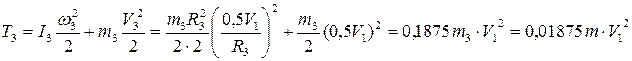

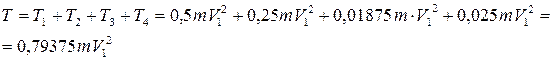
кинетическая энергия системы
3. Работа внешних сил
 - работа силы тяжести тела 1
- работа силы тяжести тела 1
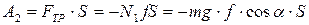 - работа силы трения тела 1
- работа силы трения тела 1
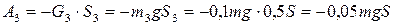 - работа силы тяжести тела 3
- работа силы тяжести тела 3
 - работа силы тяжести тела 4
- работа силы тяжести тела 4
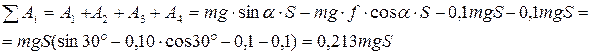 - сумма работ
- сумма работ
4. Определим скорость тела 1
по теореме об изменении кинетической энергии системы

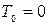
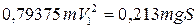
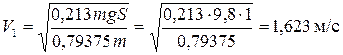
Ответ: 
Задание 7.
При кинематическом анализе решаются следующие задачи:
• Определение положений звеньев механизма при заданном положе-
нии входного звена.
• Определение линейных скоростей точек механизма и угловых скоро-
стей звеньев.
• Определение линейных ускорений точек механизмов и угловых ус-
корений звеньев.
• Определение функций положений звеньев, первых и вторых переда-
точных функций механизма.
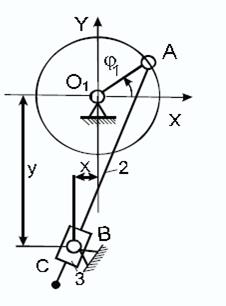
Рисунок 7.1
Дано: φ1 = 120°; ω1 = 50 с-1; О1А = 0,05 м; АС = 0,24 м; х = 0,007 м; y = 0,12 м
Решение:
Механизм состоит из входного звена (кривошипа О1А) и присоединенной к нему и к стойке группы Ассура 2-го класса 3-й модификации 2-го вида (диада ВПВ). В данном механизме группа присоединяется шатуном к входному звену, а ползуном к стойке.
Строим план положений механизма в масштабе KL = 0,002 м/мм (рис. 7.2.)

Рисунок 7.2.
Масштаб плана скоростей
Определим скорость точки А, принадлежащей кривошипу:
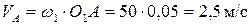
Отложим на чертеже от произвольно выбранной точки PV, которая называется полюсом плана скоростей, вектор 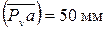 , соответствующий скорости точки А. Тогда масштаб плана скоростей определится следующим образом:
, соответствующий скорости точки А. Тогда масштаб плана скоростей определится следующим образом:
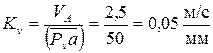
Масштаб плана ускорений
Определим ускорение точки А.
Так как ω1 = const, то ε1 = 0 и полное ускорение входного звена механизма равно нормальному ускорению
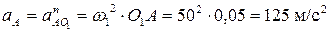
Отложим на чертеже от произвольно выбранной точки Pa, которая называется полюсом плана ускорений, вектор 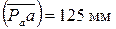 , соответствующий ускорению точки А. Тогда масштаб плана ускорений определится следующим образом:
, соответствующий ускорению точки А. Тогда масштаб плана ускорений определится следующим образом:
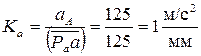
Рассматриваем кинематический анализ механизма, в котором шатун 2 присоединяется вращательной парой А к кривошипу 1. Ползун 3 присоединяется вращательной парой В к стойке.
Данный механизм при структурном анализе распадается на следующие группы Ассура.
Стойка – О1 –1 → 1-й класс,
Авр – 2 – Bпост –3 – Ввр, 2-й класс, 3-я мод. 2-й вид (диада ВПВ).
Перепишем запись структурного анализа с учетом нумерации звеньев
А1,2 – 2 – В2 –3 – B 3,0
Задача кинематического анализа механизма определить для заданного положения механизма следующие параметры:
– скорость VA1,2 и ускорение αА1,2 точки А1,2;
– скорость V B2 и ускорение αB2 точки В2;
– скорость VC и ускорение αC точки С;
– угловую скорость ω2 и угловое ускорение ε2 шатуна АС;
– угловую скорость ω3 и угловое ускорение ε3 ползуна.
Следует заметить, что скорость и ускорение точки С могут быть определены только после определения скорости и ускорения точки В2
Построение плана скоростей механизма (рис. 7.3)
Кинематический анализ механизма начинаем с входного звена и далее в порядке присоединения групп Ассура.
Входное звено O1A – (кривошип)
Точка А1 принадлежит кривошипу (звено 1), и ее скорость определяется по зависимости
 .
.
Вектор этой скорости направлен в сторону угловой скорости ω1 по касательной к траектории, т. е. перпендикулярно к радиусу О1А.
С учетом масштаба КV величина вектора 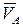 равна
равна
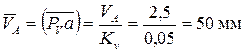
Присоединенная группа А2 – 2 – В2 –3 – B 3,0
В точке А вращательной парой соединяются кривошип (звено 1) и шатун (звено 2), поэтому 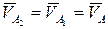 . В точке В вращательной парой соединяются ползун (звено 3) и стойка (звено 0). Скорость точки В0, принадлежащей стойке, равна нулю:
. В точке В вращательной парой соединяются ползун (звено 3) и стойка (звено 0). Скорость точки В0, принадлежащей стойке, равна нулю: 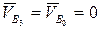
В точке В поступательной парой соединяются шатун (звено 2) и ползун (звено 3), следовательно: 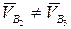 . Скорость точки В2 подлежит определению.
. Скорость точки В2 подлежит определению.
Движение шатуна рассматриваем как сложное движение, состоящее из переносного поступательного движения вместе с точкой (полюсом) А2, скорость которой известна, и относительного вращательного движения вокруг полюса А2 со скоростью 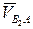 .
.
Тогда в соответствии с теоремой сложения скоростей при сложном движении для точки В2 имеем:
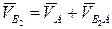
где 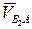 – относительная скорость точки В2 по отношению к полюсу А.
– относительная скорость точки В2 по отношению к полюсу А.
При построении векторного уравнения вектор относительной скорости 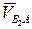 не может быть построен, так как для него известна только линия действия
не может быть построен, так как для него известна только линия действия 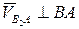 , но неизвестны величина и направление (ω2 – неизвестна).
, но неизвестны величина и направление (ω2 – неизвестна).
Движение шатуна 2 можно представить как переносное вращательное движение вместе с ползуном 3 и относительное поступательное движение по
отношению к ползуну со скоростью 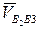 :
:
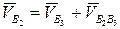
где 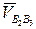 – относительная скорость точки В2 по отношению к точке В3, принадлежащей ползуну.
– относительная скорость точки В2 по отношению к точке В3, принадлежащей ползуну.
При построении векторного уравнения вектор относительной скорости 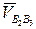 не может быть построен, так как для него известна только линия действия
не может быть построен, так как для него известна только линия действия  , но неизвестны величина и направление.
, но неизвестны величина и направление.
Объединяем уравнения в систему
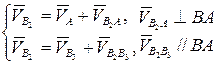
Эту систему будем решать графически. Цель построения – определить скорость точки В2.
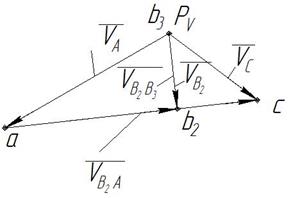
Рисунок 7.3
Построение плана скоростей производится в следующей последовательности:
1. Выберем полюс плана скоростей РV -– общее начало векторов абсолютных скоростей точек механизма.
2. Из полюса РV построим вектор скорости точки А в масштабе KV:
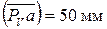
Конец вектора обозначим буквой а.
3. Согласно первому уравнению системы, из конца вектора 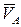 , т. е. через точку а, проведем линию действия относительной скорости
, т. е. через точку а, проведем линию действия относительной скорости
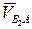 перпендикулярно звену AB,
перпендикулярно звену AB, 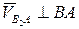 .
.
4. Согласно второму уравнению системы, из полюса РV (так как 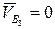 ) проведем линию действия относительной скорости
) проведем линию действия относительной скорости 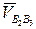 параллельно звену
параллельно звену 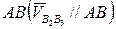 .
.
Отметим точку пересечения двух линий действия относительных скоростей и обозначим ее b2.
Проведем из полюса РV вектор в точку b2 – это вектор абсолютной скорости точки В2. Проведем вектор из точки b3, которая находится в полюсе РV, в точку b2 – это вектор относительной скорости точки В2 по отношению к точке В3.
Чтобы получить модули этих скоростей в размерности мс–1, необходимо измерить вектор в мм и умножить на масштаб KV:
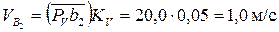
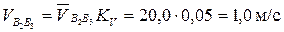
Скорость точки С, принадлежащей кулисе АС, может быть получена по теореме подобия плана скоростей:
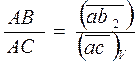 ; отсюда
; отсюда 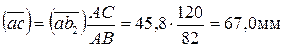 .
.
Отложим на плане скоростей от а отрезок 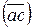 , на отрезке
, на отрезке 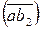 и обозначим конец отрезка точкой с. Из полюса РV проведем вектор в точку с.
и обозначим конец отрезка точкой с. Из полюса РV проведем вектор в точку с.
Это вектор – абсолютная скорость точки С в масштабе KV.
Чтобы получить модуль этой скорости в размерности м/с, необходимо измерить вектор 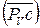 в миллиметрах и умножить на масштаб KV:
в миллиметрах и умножить на масштаб KV:
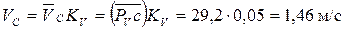 .
.
Определение величины и направления угловых скоростей звеньев механизма
Звено 1 – входное звено О1А (кривошип).
Угловая скорость кривошипа определяется по следующей зависимости
ω1 = 50 с–1,
Направление угловой скорости кривошипа ω1 против часовой стрелки.
Звено 2 – шатун АВ.
Величина угловой скорости звена АВ определяется по формуле
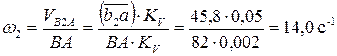
где 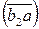 – длина отрезка на плане скоростей, мм;
– длина отрезка на плане скоростей, мм;
KV – масштаб плана скоростей, мс–1/мм;
ВА – длина шатуна, измеренная на плане положений от точки А до точки В, м.
Для определения направления угловой скорости ω2 остановим на механизме точку А, перенесем с плана скоростей вектор 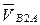 в точку В и проследим какому направлению угловой скорости ω2 соответствует вектор скорости
в точку В и проследим какому направлению угловой скорости ω2 соответствует вектор скорости 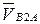 . Этой скорости на рис. 7.3 соответствует вращение звена ВА против часовой стрелки. Следовательно, ω2 будет направлена против часовой стрелки.
. Этой скорости на рис. 7.3 соответствует вращение звена ВА против часовой стрелки. Следовательно, ω2 будет направлена против часовой стрелки.
Звено 3-ползун.
Угловая скорость ползуна по величине и направлению равна угловой скорости звена 2, ω3 = ω2.
Составление векторных уравнений и расчетных зависимостей для построения планов ускорений
Построение планов ускорений производится так же, как и план скоростей в порядке наслоения групп Ассура.
Входное звено О1А – (кривошип)
Полное ускорение точки А при ω1 = const определяется по зависимости
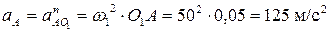
Вектор ускорения 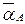 направлен параллельно звену O1A от точки А к точке O1. С учетом масштаба Ка величина вектора
направлен параллельно звену O1A от точки А к точке O1. С учетом масштаба Ка величина вектора 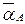 равна
равна
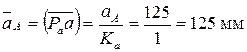
Присоединенная группа А1,2 – 2 – В2 –3 – B3,0
В точке А шарнирно соединяются звено 1 и звено 2, поэтому ускорения 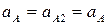 . Ползун 3 соединяется вращательной парой В со стойкой, поэтому
. Ползун 3 соединяется вращательной парой В со стойкой, поэтому 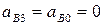 . В точке В шатун 2 поступательной парой присоединяется к ползуну 3, поэтому aB2 ≠ aB3. Подлежит определению aB2 .
. В точке В шатун 2 поступательной парой присоединяется к ползуну 3, поэтому aB2 ≠ aB3. Подлежит определению aB2 .
Движение кулисы ВА рассматриваем как сложное движение, состоящее из переносного движения вместе с точкой (полюсом) А, ускорение которой известно, и относительного вращательного движения вокруг полюса А.
Тогда в соответствии с теоремой сложения ускорений при сложном движении для точки В2 получаем
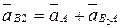
где  – относительное ускорение точки В2 вокруг полюса А.
– относительное ускорение точки В2 вокруг полюса А.
При построении векторного уравнения вектор относительного ускорения 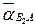 не может быть построен, так как его величина и направление неизвестны.
не может быть построен, так как его величина и направление неизвестны.
Движение шатуна ВА рассматриваем как сложное движение, состоящее из переносного вращательного движения вместе с ползуном 3, для которого ускорение точки В3 известно (aB3 = aB0 = 0) и относительного ускорения 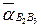 при поступательном движении шатуна по отношению к ползуну 3, для которого неизвестны величина и направление.
при поступательном движении шатуна по отношению к ползуну 3, для которого неизвестны величина и направление.
Если при движении точки на плоскости имеет место вращательное переносное движение и относительное поступательное, то возникает дополнительное ускорение, которое называется кориолисовым.
В соответствии с теоремой сложения ускорений при сложном движении для точки В2 имеем
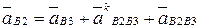
Разложим относительные ускорения 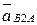 и
и  на нормальные и касательные составляющие и объединим в систему уравнения:
на нормальные и касательные составляющие и объединим в систему уравнения:
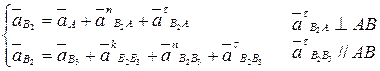
Величины нормальных ускорений и кориолисово ускорение определяются по известным зависимостям, а касательные ускорения известны по линии действия:
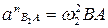 или
или 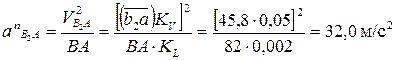
Чтобы определить размер вектора этого ускорения необходимо модуль ускорения 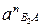 разделить на масштаб Ka:
разделить на масштаб Ka:
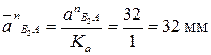
Ускорение  направляется по звену ВА от В к А. Касательное ускорение
направляется по звену ВА от В к А. Касательное ускорение 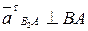
Вектор нормального ускорения 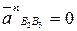 , так как относительное движение шатуна и ползуна – прямолинейное. Линия действия касательного ускорения
, так как относительное движение шатуна и ползуна – прямолинейное. Линия действия касательного ускорения 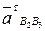 направлена по касательной к траектории относительного движения
направлена по касательной к траектории относительного движения 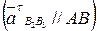 .
.
Величина кориолисова ускорения для плоского движения определяется по формуле:

Для данного случая ωпер = ω3 и Vотн = VB2B3.
Следовательно, 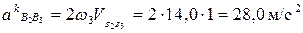
Чтобы определить размер вектора 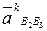 в миллиметрах, необходимо его модуль разделить на масштаб Ka:
в миллиметрах, необходимо его модуль разделить на масштаб Ka:

Вектор 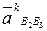 будет направлен в ту сторону, в которую будет направлен вектор относительной скорости
будет направлен в ту сторону, в которую будет направлен вектор относительной скорости 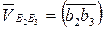 при повороте его на 90° по направлению угловой скорости переносного движения ω3.
при повороте его на 90° по направлению угловой скорости переносного движения ω3.
Построение плана ускорений (рис. 7.4) производится в следующей последовательности:
1. Выберем полюс плана ускорений Ра – общее начало векторов абсолютных ускорений точек механизма.
2. Из полюса Ра построим вектор ускорения точки А в масштабе Ka,
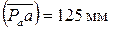 . Конец вектора обозначим а
. Конец вектора обозначим а
3. Из точки а строим вектор 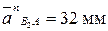 , который направлен по звену 2 от В к А:
, который направлен по звену 2 от В к А:  . Через конец этого вектора проводим линию действия касательного ускорения
. Через конец этого вектора проводим линию действия касательного ускорения  .
.
4. Согласно второму уравнению системы, из полюса Ра (первый вектор уравнения 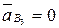 ), строим вектор кориолисова ускорения
), строим вектор кориолисова ускорения 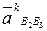 ,известный по величине и направлению, и через его конец проводим линию действия касательного ускорения
,известный по величине и направлению, и через его конец проводим линию действия касательного ускорения 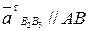 .
.
5. Отметим точку пересечения двух линий действия касательных ускорений 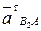 и
и 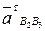 и обозначим ее b2;
и обозначим ее b2;
6. Проведем из полюса  вектор в точку b2 – это вектор абсолютного ускорения
вектор в точку b2 – это вектор абсолютного ускорения 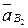 точки В2.
точки В2.
Вектор относительного ускорения 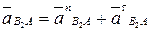 . Вектор относительного ускорения
. Вектор относительного ускорения 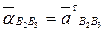 .
.
Чтобы получить модули этих ускорений в размерности м/с2 необходимо измерить соответствующие векторы в миллиметрах и умножить на масштаб Ka:

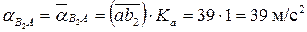
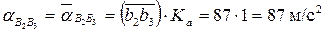
Ускорение точки С, принадлежащей звену АС, определяется с применением теоремы подобия:
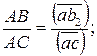 отсюда
отсюда 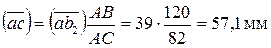
Отложим на плане ускорений от точки а отрезок 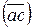 по линии действия вектора
по линии действия вектора 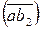 и соединим полученную точку с с полюсом Ра. Этот отрезок представляет собой вектор
и соединим полученную точку с с полюсом Ра. Этот отрезок представляет собой вектор 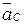 в масштабе Ka.
в масштабе Ka.
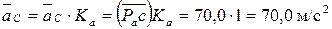
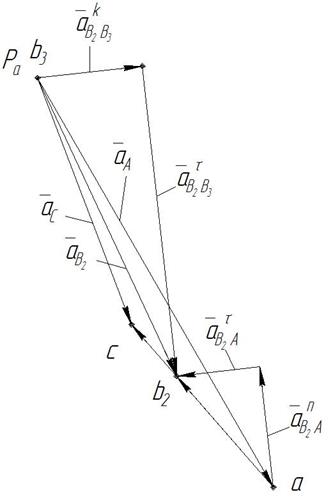
Рисунок 7.4