Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
Жидкость в неинерциальных системах отсчета
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.15).
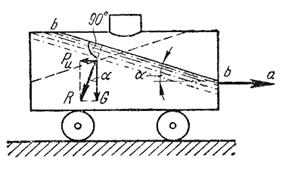
Рис. 2.15. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G=mg и сила инерции Pu = ma.
Равнодействующая этих сил R = ((mg)2+(m a)2)1/2 направлена к вертикали под углом α, тангенс которого равен tga = a /g.
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости.
Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).
Относительный покой жидкости во вращающемся сосуде
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (рис.2.16), например, в сепараторах и центрифугах, применяемых для разделения жидкостей.
В этом случае на любую частицу жидкости при ее относительном равновесии действуют массовые силы:
сила тяжести G=mg
центробежная сила Pц=mω2r,
где r - расстояние частицы от оси вращения, а ω - угловая скорость вращения сосуда.

Рис. 2.16. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом, который описывается уравнением

Закон изменения давления во вращающейся жидкости в функции радиуса и высоты записывается в виде

Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
Равновесие газа
Уравнения равновесия, выведенные для жидкости, имеют общий характер и могут быть использованы при расчете сжимаемой жидкости или газа.
Для газа, находящегося в равновесии, любая горизонтальная плоскость, проведенная внутри занимаемого газом объема, будет поверхностью равного давления (рис. 2.11).
В однородной газовой среде (ρ = const), распределение давления не отличается от распределения давления в покоящейся капельной жидкости.
Действительно при Х=0, У=0 и Z=- g.
dp = -ρgdz; (2.17)
p = -ρgz+C, C = p 0 + ρgz 0
Определив постоянную интегрирования из граничных условий, например (см. рис. 2.11) на поверхности земли z=z0 и р=р0,получим уравнение
р = p0 + ρg(z0 - z), (2.18)
где z - расстояние от плоскости сравнения 0'-0' до рассматриваемой точки (высота точки М); z0 - расстояние от плоскости сравнения 0'-0' до поверхности с заданным давлением р=р0.

Рис. 2.11. Равновесие газа в поле силы тяжести
Уравнения (2.17) и (2.18) показывают, что в поле силы тяжести изменение давления газа будет, так же как и в капельной жидкости, определяться только изменением расстояния от плоскости сравнения до рассматриваемой точки. Полученное уравнение показывает, что с увеличением высоты до рассматриваемой точки давление уменьшается, так как в выбранной системе координат z>z0.
Характер же этого изменения будет корректироваться в зависимости от закона изменения внутреннего состояния газа.