Числовые пары
Пример:
(1;2),(2;4),(3;6)
Линейная функция, свойства и график.
Линейная функция – это функция, которую можно задать формулой y=kx+m, где x – независимая переменная, k и m – некоторые числа.
Применяя эту формулу, зная конкретное значение x, можно вычислить соответствующее значение y.
Пусть y=0,5x−2.
Тогда:
если x=0, то y=−2;
если x=2, то y=−1;
если x=4, то y=0 и т.д.
Обычно эти результаты оформляют в виде таблицы:
| x | |||
| y | −2 | −1 |
x - независимая переменная (или аргумент),
y - зависимая переменная.
Графиком линейной функции y=kx+m является прямая.
Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.
Построим на координатной плоскости xOy точки (0;−2) и (4;0) и
проведём через них прямую.
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции.
Составим таблицу значений функции:
| x | −3 | |
| y | −3 |
Построим на координатной плоскости xOy точки (−3;7) и (2;−3) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции y=−2x+1,x∈[−3;2].
Точки (−3;7) и (2;−3) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения x=−3 и x=2 не рассматриваются, так как они не принадлежат интервалу (−3;2).
Поэтому точки (−3;7) и (2;−3) на рисунке отмечены светлыми кружочками.
Рассматривая график линейной функции на отрезке, можно назвать наибольшее и наименьшее значение линейной функции.
В случае
a) y=−2x+1,x∈[−3;2] имеем, что yнаиб=7 и yнаим=−3,
b) y=−2x+1,x∈(−3;2) имеем, что ни наибольшего и ни наименьшего значений линейной функции нет, так как оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, исключены из рассмотрения.
В ходе построения графиков линейных функций, можно как бы «подниматься в горку» или «спускаться с горки», т.е. линейная функция или возрастает или убывает.
Если k>0, то линейная функция y=kx+m возрастает;
если k<0, то линейная функция y=kx+m убывает.
10. Прямой пропорциональностью называется функция, которую можно задать формулой y = kx, где х – независимая переменная, k – не равное нулю
действтельное число. Число k называют
коэффициентом прямой пропорциональности.
График прямой пропорциональности представляет собой
прямую, проходящую через начало координат, чтобы его построить, достаточно отметить только еще одну точку и соединить ее и начало координат прямой. (см.рисунок).
Прямая пропорциональность является частным случаем
линейной функции.
Свойства функции y = kx:
1. Область определения функции и область значения - множество всех действительных чисел.
2. Графиком прямой пропорциональности является
прямая, проходящая через начало координат
3. При к>0 функция у=кx возрастает на всей области
определения; при к<0 убывает на всей области определения.
4. Это нечетная функция.
5. Переменные изменяются прямо пропорционально
на всей числовой прямой: при возрастании аргумента
функция пропорционально возрастает, при убывании
аргумента функция пропорционально убывает.
6.Если функция f-прямая пропорциональность, то она
может быть задана формулой у=кx, и тогда у1=кx, y2=kx2
В случае с графиком k– это угловой коэффициент. Если угловой коэффициент меньше нуля (k < 0), то угол между графиком функции прямой пропорциональности и осью абсцисс тупой, а функция убывающая. Если угловой коэффициент больше нуля (k > 0), график и ось абсцисс образуют острый угол, а функция – возрастающая.
11. Обратной пропорциональностью
называется функция вида
где 
и является числом.
Графиком функции является гипербола.
Свойства функции
1) Областьюопределения функции 
является множество всех действительных чисел, кроме x=0, т.е. 
2) Множеством значений функции являются все числа, кроме y=0, т.е. промежуток 
3) Наименьшего и наибольшего значений функция не имеет.
4) Функция является нечетной, график симметричен относительно начала координат (0; 0)
5) Функция непериодическая.
6) График функции не пересекает координатных осей.
7) Функция не имеет нулей.
8) Функция 
на каждом из промежутков 
является убывающей.
Функция 
на каждом из промеж. является возрастающей.
12. Квадратичной (квадратной) функцией называется функция вида
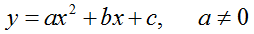
где a, b, с - числа.
Графиком квадратичной функции является парабола.
Свойства
1) Областью определения функции 
является множество всех действительных чисел, т.е.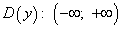 
2) Множеством значений функции является промежуток 
3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.
4) Функция является четной, график симметричен относительно оси Оу.
5) Функция непериодическая.
6)Парабола имеет с осями координат единственную общую точку (0;0) - начало координат.
7) Значение аргумента x=0 является нулем функции.
8) На промежутке 
функция убывающая, а на промежутке 
- возрастающая.
13.Дробно-линейная функция – это функция вида
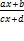где x – переменная, a, b, c, d – некоторые числа, причем c ≠ 0,
Графиком дробно-линейной функции является гипербола, которую можно получить из гиперболы y = k/x с помощью параллельных переносов вдоль координатных осей.
Свойства дробно-линейной функции:
1. При возрастании положительных значений аргумента значения функции убывают и стремятся к нулю, но остаются положительными.
2. При возрастании положительных значений функции значения аргумента убывают и стремятся к нулю, но остаются положительными.
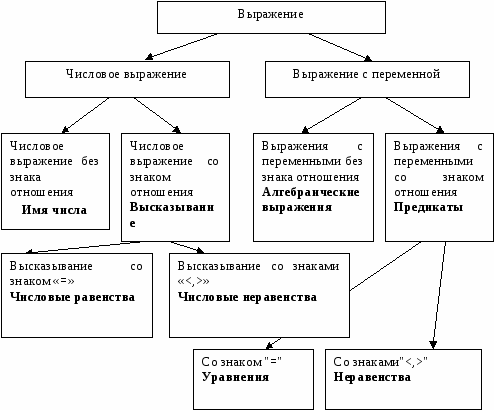
14. Выражение. Классификация выражений.
Выражение - это последовательность операций. Выражение может быть классифицировано одним из следующих образов:
· Значение. Каждое значение имеет связанный с ним тип.
· Переменная. Каждая переменная имеет связанный с ней тип, а именно тип указанный при определении переменной.
· Пространство имен. Выражение, классифицированное данным образом, может появляться только в левой части доступа к члену.
· Тип. Выражение, классифицированное данным образом, может появляться только в левой части доступа к члену.
· Группа методов, которая получается в результате процесса поиска члена.
· Доступ к свойству. Каждое выражение, классифицированное как доступ к свойству, имеет связанный с ним тип, а именно тип свойства.
· Доступ к событию. Каждое выражение, классифицированное как доступ к событию, имеет связанный с ним тип, а именно тип события (делегат). Пустое. Данная ситуация возникает когда выражение является вызовом метода не имеющего возвращаемого значения. Конечный результат выражения никогда не является пространством имен, типом, группой методов или доступом к событию. Данные категории выражений являются лишь промежуточными конструкциями допустимыми в определенных контекстах.
Числовое выражение и его значение.
Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок. Числовое выражение может состоять и просто из одного числа. Основными арифметическими действиями являются «сложение», «вычитание», «умножение» и «деление». Этим действиям соответствуют знаки «+», «-», «∙», «:».
Конечно же, чтобы у нас получилось числовое выражение, запись из чисел и арифметических знаков должна быть осмысленной. Так, например, такую запись 5: + ∙ нельзя назвать числовым выражением, так как это случайный набор символов, не имеющий смысла. Напротив, 5 + 8 ∙ 9 - уже настоящее числовое выражение.
Значение числового выражения.
Сразу скажем, что если мы выполним действия указанные в числовом выражении, то в результате мы получим число. Это число называется значением числового выражения.
Числовое равенство: 5 + 8 ∙ 9 = 77. Если значения левой и правой части равенства совпадают, то равенство называют верным. 5 + 8 ∙ 9 = 77 – верное равенство.
Если 5 + 8 ∙ 9 = 100, то это уже будет неверное равенство, так как значения левой и правой части данного равенства уже не совпадают.
Числовое неравенство – это неравенство, в записи которого по обе стороны от знака неравенства находятся числа или числовые выражения.
Свойства числовых неравенств
1) если к обеим частям истинного числового неравенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое неравенство (А < В Þ (А) + (С) < (В) + (С));
2) если обе части истинного числового неравенства умножить на одно и то же числовое выражение, имеющее смысл и принимающее положительное значение, то полученное числовое неравенство будет также истинным (А < В Þ (А) ∙ (С) < (В) ∙ (С));
3) если обе части истинного числового неравенства умножить на одно и то же числовое выражение, имеющее смысл и принимающее отрицательное значение, то, чтобы получить истинное числовое неравенство, необходимо знак неравенства поменять на противоположный (А < В Þ (А) ∙ (С) > (В) ∙ (С));
4) неравенства одного знака можно почленно складывать (А < В, С < D Þ (А) + (С) < (В) + (D));