Подбор эмпирических формул
Постановка задачи
При интерполяции используется условие равенства значений интерполяционного многочлена и заданной функции в известных точках (узлах интерполяции). При обработке опытных данных выполнение этого условия нецелесообразно, так как они получены с некоторой погрешностью. Погрешность вызвана несовершенством измерительного прибора, субъективными причинами, различными случайными факторами и т.д.
Построение аппроксимирующего многочлена с условием обязательного прохождения его графика через экспериментальные точки означает повторение допущенных при измерении ошибок. Выход из этого положения может быть найден выбором такого многочлена, график которого проходит близко от экспериментальных точек. Понятие «близко» уточняется при рассмотрении различных видов приближения (аппроксимации).
Одним из таких видов является среднеквадратичное приближение функций с помощью аппроксимирующего многочлена
φ (х)= 
, (5.1)
где m – степень многочлена [8, 18].
При среднеквадратичном приближении m < n. Здесь n +1 – количество опытных точек. Случай m = n +1 соответствует глобальной интерполяции. На практике стараются подобрать аппроксимирующий многочлен как можно меньшей степени. Как правило, m = 1, 2, 3.
Аппроксимирующий многочлен называют также эмпирической формулой. Это формула, полученная путем описания (приближения) опытных данных.
Графики интерполяционного и аппроксимирующего многочленов показаны на рис. 5.1. На этом рисунке εi - отклонение между опытным значением функции (yiэ) и аппроксимирующим многочленом (yi = φ (хi)) в точке xi, т.е.
.
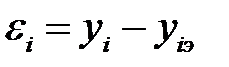Рис. 5.1. Интерполяция и среднеквадратичное приближение (аппроксимация):
A, B, C, D, Е - опытные точки; 1 – график интерполяционного многочлена;
2 - график аппроксимирующего линейного многочлена (коэффициенты
найдены среднеквадратичным приближением)
Мерой отклонения многочлена φ (х) от заданной функции f (х) на множестве точек (хi, yi) (i = 0, 1, 2, …, n) при среднеквадратичном приближении является величина S:
, (5.2)
где S - сумма квадратов отклонений между значениями многочлена и функции в данных точках (или сумма квадратов отклонений между опытными данными и рассчитанными по формуле (5.1)); yiэ – опытные значения функции f (x) при х = хi.
Для построения аппроксимирующего многочлена (эмпирической формулы) (5.1) коэффициенты a0, а1 , …,аm нужно подобрать так, чтобы величина S была наименьшей. В этом состоит суть метода наименьших квадратов.
Виды эмпирических формул
Пусть мы изучаем неизвестную функциональную зависимость между у и х. Например, у - предел прочности стали σв, х - температура t нагрева образцов при испытании на растяжение. Таким образом, σв = f (t). В результате выполнения эксперимента провели n измерений этих величин и данные записали в табл. 5.1.
Таблица 5.1
Пример таблицы с опытными данными
| х 0 | х 1 | х 2 | … | х i | … | х n |
| у 0э | y 1э | у 2э | … | у iэ | … | у nэ |
Задача состоит в том, чтобы найти приближенную зависимость
(5.3)
значения которой при х = хi (i = 0, 1,…, n) мало отличаются от опытных данных yiэ.
Приближенная функциональная зависимость (5.3), полученная на основании экспериментальных данных, называется эмпирической формулой. График эмпирической зависимости не проходит через опытные точки (хi, yi) как в случае интерполяции. Это приводит к тому, что экспериментальные данные в некоторой степени сглаживаются.
Построение эмпирической формулы состоит из двух этапов [7, 9]:
а) подбор общего вида этой формулы;
б) определение наилучших значений содержащихся в ней параметров.
Общий вид формулы иногда известен из физических соображений. Например, для упругой деформации связь между напряжением σ и относительной деформацией ε определяется законом Гука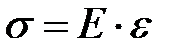 
. Здесь Е - модуль упругости. Задача сводится к определению одного неизвестного параметра Е.
Если характер зависимости неизвестен, то вид эмпирической формулы может быть произвольный. Предпочтение обычно отдается наиболее простым формулам, обладающим достаточной точностью. Они первоначально выбираются из геометрических соображений: экспериментальные точки наносятся на график и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиком известных функций. Это может быть многочлен, показательная функция, логарифмическая функция и т.д. Успех здесь в значительной мере определяется опытом и интуицией исследователя.
Простейшей эмпирической формулой является линейная зависимость
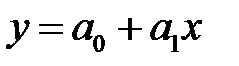. (5.4)
Формула квадратного трехчлена
. (5.5)
Степенная функция
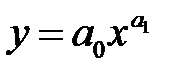. (5.6)
На рис. 5.2 приведен пример данных, когда экспериментальные точки расположены вблизи графика степенной функции. Поэтому следует использовать эмпирическую формулу вида (5.6).
Рис. 5.2. Пример расположения опытных точек на графике
Будем считать, что тип эмпирической формулы выбран и ее можно
записать в общем виде следующим образом:
, (5.7)
где φ - известная функция; 
- неизвестные постоянные параметры.
Величины этих параметров должны быть такими, чтобы эмпирическая формула (5.7) давала хорошее приближение к экспериментальным значениям yiэ . Значения эмпирической функции (5.7) в точках хi будем обозначать yi, т.е.:
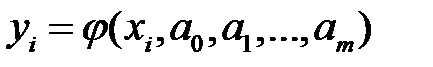. (5.8)
Напомним, что yiэ - экспериментальные значения, а yi - расчетные значения функции.
Отклонения yi от yiэ будем обозначать εi, т.е.:
(5.9)
где i = 0,1,…, n; n +1 - количество опытных точек; m +1 - количество членов в эмпирической формуле.
Задача нахождения наилучших значений параметров 
сводится к некоторой минимизации отклонений εi. Существует несколько способов решения этой задачи. Мы рассмотрим метод наименьших квадратов (МНК).