ГРУППЫ И ИХ ПРОСТЕЙШИЕ СВОЙСТВА

Будем говорить что на множестве G определена бинарная операция *, если любой упорядоченной паре (a,b) элементов 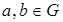ставится в соответствие однозначно определённый элемент 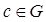, что записывается в виде c=a * b.

В учебной литературе понятие группы вводится различными способами. Начинающим рекомендуем использовать следующее

Определение 1. Множество (G, *) называется группой относительно бинарной операции *, если выполнены следующие условия:

1) операция * определена на множестве G

2) операция * ассоциативна: (a * b)* c = a *(b * c) для любых ;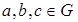

3) в G существует нейтральный элемент, т.е. такой элемент e что 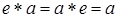для всех ;

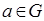4) для каждого элемента 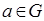существует обратный элемент 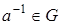, такой, что .

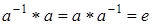Множество А называется моноидом, если выполняются первые три указанные условия; полугруппой, если выполняются первые два условия; группоидом, если выполняется первое условие.

Обратим внимание на то, что операция в группе не обязательно является коммутативной.

Определение 2. Группа называется коммутативной (или абелевой – в честь выдающегося математика Абеля), если операция в этой группе коммутативна, то есть a * b = b * a для любых .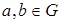

Определенность операции на множестве A означает, что для каждой пары элементов из A результат операции, во-первых, существует, а во-вторых – также принадлежит A. Так, операция деления не определена на множестве всех целых чисел, потому что, например, не существует элемента 1/0; операция деления не определена на множестве всех натуральных чисел, так как, например, число 2/3 хотя и существует, но оно не является натуральным; операция деления определена на множестве всех положительных рациональных чисел, так как для любых положительных рациональных чисел a и b результат операции a: b существует и также является положительным рациональным числом.

Вместо фразы «операция определена на множестве А » употребляют также фразу «множество А замкнуто относительно данной операции» или «операция является алгебраической на множестве А ». Говорить о замкнутости множества А относительно данной операции особенно целесообразно тогда, когда относительно существования результата операции нет сомнения.

Если операция в группе – сложение, то такая группа называется аддитивной; если же операция – умножение, то такая группа называется мультипликативной.

Ассоциативный закон имеет вид a+(b+c)=(a+b)+c в аддитивной записи и a×(b×c)=(a×b)×c – в мультипликативной записи.

Нейтральный элемент аддитивной группы называется нулем и обозначается 0: 0+ a = a, a +0= a. Нейтральный элемент мультипликативной группы называется единицей и обозначается 1: 1× a=a, a× 1= a.

Если элемент е удовлетворяет условию е*a=a для каждого a группоида, то е называется левым нейтральным элементом. Аналогично определяется правый нейтральный элемент. Если в группоиде существуют левый и правый нейтральные элементы, то они совпадают, и можно говорить о нейтральном элементе.

Проверка того, что множество А относительно операции * образует группу, сводится к проверке выполнения условий (аксиом) (1)-(4) в определении 1. Так, (Q,:) не является группой, поскольку уже первая аксиома не выполняется: результат 1:0 не определен. Для множества всех рациональных чисел без нуля Q ^* операция деления определена, но не выполняется ассоциативный закон: a:(b:c)¹(a:b):c.

Хотя для множества четных чисел 2Z операция умножения определена (произведением четных чисел является четное число), и она является ассоциативной, но это множество не содержит нейтрального элемента и группу не образует, а является полугруппой.

Так, например, (N, ×) – моноид, т.е. множество всех натуральных чисел относительно умножения удовлетворяют аксиомам (1)-(3), но это не группа, поскольку не выполняется аксиома (4).

Нетрудно убедиться, что группами являются (Q^*, ×), (R,+), (R [ x ],+), (M₂,+), (C, +), (GL(n,R), ×).

Пример 1. Выяснить, является ли группой относительно операции 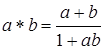каждое из следующих множеств: а) R – множество действительных чисел; б) 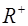– множество положительных действительных чисел; в) множество A = (-1; 1).

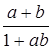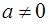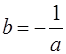а) Дробь существует только при . На множестве R, если , а , то 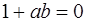, и поэтому операция * определена не для всех действительных чисел (например, для пары чисел -1 и 1), значит (R, *) – не является группой.

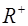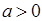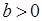б) Операция * определена на , т. к. для всех и дробь 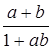существует и положительна. Операция * является ассоциативной: .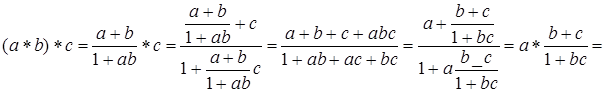

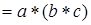Нейтральный элемент e определяется из условий e * a = a * e = a для всех 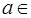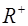. Тогда 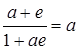, что равносильно 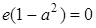, откуда e =0. Но число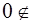 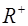, поэтому (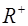, *) является полугруппой, но не группой.

в) операция * определена на A, т.к. для всех 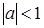и 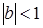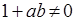, выполняются неравенства 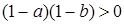и 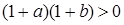, которые равносильны, соответственно, 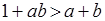и 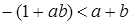, т. е. 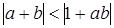. Поэтому 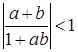и .

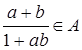Операция * является ассоциативной (проверено выше), нейтральный элемент .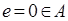

Обратный для a элемент x должен удовлетворять условию

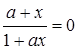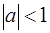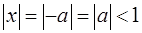x * a = a * x = 0 или , откуда x = – a. Если , то и 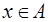, т. е. Все элементы множества A обратимы.

Следовательно (A, *) – группа. Очевидно, что a * b = b * a для всех 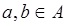, поэтому (A, *) – абелева группа.

Пример 2. Пусть Н = 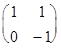. Образует ли группу относительно операции А*В=АВН множество всех (2´2) матриц над R вида:

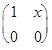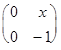а) ; б) ; в) ?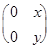

а) А * В= * = = .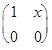

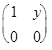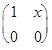
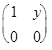
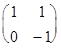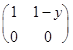Операция определена на множестве и ее действие сводится к действиям над над числами: x*y=1-y.

Проверка показывает, что в случае а) операция не является ассоциативной: (x*y)*z=(1-y)*z=1-z; x*(y*z)=x*(1-z)=1-(1-z)=z.

б) А*В= * = = .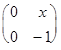

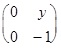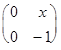
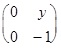
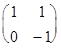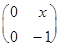Получилось, что А*В=А. Эта операция является ассоциативной, поскольку (А*В)*С=В*С=С и А*(В*С)=А*С=С. Очевидно, каждая матрица является правой единицей, в то время, как левых единиц нет вообще. Таким образом, мы имеем полугруппу, но не группу.

в) А*В = * = = .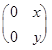

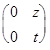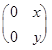
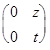
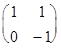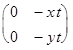Операция, очевидно, определена на данном множестве, и ее действие сводится к действию над упорядоченными парами чисел: (x, y)*(z, t)=(-xt, -yt).

Операция является ассоциативной, поскольку

((x, y)*(z, t))*(u, v)=(-xt, -yt)*(u, v)=(xtv, ytv),

(x, y)*((z, t)*(u, v))=(x, y)*(-zv, -tv)=(xtv, ytv).

Все матрицы вида 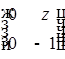являются правыми единицами, а левых единиц – нет вообще.

 

КОЛЬЦА И ПОЛЯ

 

Определение 12. Множество К называется кольцом, если на нем определены две бинарные операции ²+² (сложения) и ²×² (умножения), которые удовлетворяют условиям:

1) (К,+) – абелева группа (аддитивная группа кольца);

2) (К, ×) – полугруппа (мультипликативная полугруппа кольца);

3) обе операции связаны дистрибутивными законами:

(x+y)×z=(x×z)+(y×z), z× (x+y)=(z×x)+(z×y) для всех x,y,z Î К.

Мультипликативная полугруппа кольца не обязательно коммутативна. Если же x×y = y×x для всех x, y Î К, то кольцо К называется коммутативным.

Произведение двух ненулевых элементов кольца может равняться нулю: x×y =0, x ¹0, y ¹0, при этом x и y называются, соответственно, левым и правым делителями нуля.

Если кольцо К содержит нейтральный элемент по умножению, то оно называется кольцом с единицей.

Коммутативное кольцо с единицей без делителей нуля называется целостным кольцом или областью целостности. Если кольцо содержит единицу и xy =1, или zx =1, то элементы y и z называются, соответственно, правым и левым обратным для x. Если элемент x обладает правым y и левым z обратными элементами, то y = z. В этом случае элемент x называется обратимым, и обратный к нему обозначается x ^-1: xx ^-1= x ^-1 x =1.

Все обратимые элементы кольца с единицей образуют группу относительно умножения. Её называют мультипликативной группой кольца К и обозначают К ^*.

Определение 13. Ненулевое коммутативное кольцо Р с единицей называется полем, если все его ненулевые элементы обратимы. В этом случае Р^*=Р\ {0}.

Определение 14. Отображение j: К®К ^/ кольца К на кольцо K^/ называется изоморфизмом, если отображение взаимно однозначно и сохраняет операции, то есть j(х+у)=j(х)+j(у) и j(ху)=j(х)j(у).

Два кольца называются изоморфными, если существует изоморфизм одного из них на другое.

Чтобы установить изоморфизм двух колец, достаточно найти какое-нибудь взаимно однозначное отображение одного из них на другое с сохранением операций.

Для доказательства того, что два кольца не изоморфны, следует указать какое-нибудь абстрактное свойство (то есть свойство, сохраняющееся при изоморфизмах), которым одно кольцо обладает, а другое нет. К числу таких абстрактных свойств относятся коммутативность, существование единицы, существование делителей нуля и т. д.

Определение 15. Подкольцом называется непустое подмножество А кольца К, которое само является кольцом относительно операций, определённых в К. Подкольцо, являющееся к тому же полем, называется подполем.

Для выяснения того, является ли данное подмножество подкольцом, можно пользоваться критерием подкольца: непустое подмножество кольца тогда и только тогда является его подкольцом, когда оно замкнуто относительно вычитания и замкнуто относительно умножения.

Чтобы построить подкольцо, порождённое данными элементами, нужно составить всевозможные конечные произведения этих элементов и образовать множество всех их конечных сумм и разностей.

Пример 18. Пусть дана матрица Т = 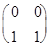. Выяснить, является ли кольцом относительно операций А Å В=А+В-Т и А 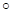В=АВ множество всех (2´2)-матриц над R следующего вида:

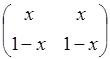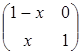а) ; б) ; в) .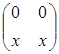

Обе операции определены на каждом из трёх данных множеств, проверим для первого из множеств 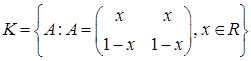(для остальных проверить самостоятельно).

Для любых матриц 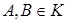А Å В=А+В-Т=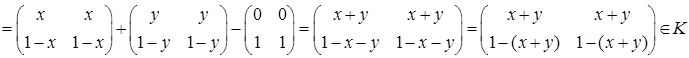

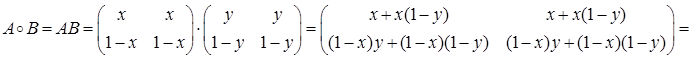
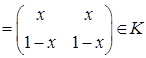
Операция Å ассоциативна:

(АÅВ)ÅС=(А+В–Т)ÅС=А+В+С–2Т;

(АÅ(ВÅС)=АÅ(В+С-Т)=А+В+С–2Т.

Очевидно, относительно операции Å матрица Т является нейтральным элементом, т. к. T Å A = А Å T=А+T-Т=A, а матрица (2Т–А) – «противоположным» элементом для А (так как АÅ(2Т-А)=Т). Кроме того, операция Å коммутативна, и каждое из трёх приведенных множеств содержит вместе с любым элементом А и его ²противоположный² 2Т-А. Операция А В=АВ – ассоциативна как обычное умножение матриц. Таким образом, доказано, что каждое из трёх множеств является абелевой группой относительно первой операции и полугруппой – относительно второй. Остаётся проверить дистрибутивность.

В случае (а) получаем, что А В=А для любых А и В. Отсюда и из того, что АÅВ=А+В-Т, имеем:

(АÅВ) С=АÅВ=А+В–Т, (А 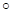С)Å(В 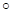С)=АÅВ=А+В–Т;

С 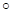(АÅВ)= С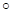, (С А)Å(С В)=СÅС=С+С–Т=2С–Т.

Следовательно, правая дистрибутивность выполняется, а левая – нет.

В случае (б) вместо действий над матрицами

A Å B = + – = ;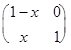

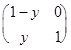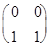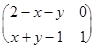А B = =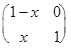

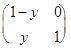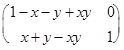
удобнее рассматривать соответствующие операции над числами (элементами матриц):

х Å у = х + у– 1; х 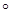у = х + у–ху.

Обе операции коммутативны, поэтому достаточно проверить лишь одну дистрибутивность, например, правую:

(x Å y)_°z=x+y+2z–xz–yz– 1 =(x_° z) Å (y_°z).

В случае (в) также вместо операций над матрицами удобнее рассматривать соответствующие операции над числами (элементами матриц): х Å у=х+у– 1; х_°у=ху. Здесь также обе операции коммутативны, но дистрибутивность нарушается:

(x Å y) _° z = xz + yz–z; (x_°z) Å (y_° z) = zx + yz– 1.

Таким образом, только в случае (б) имеем кольцо. Более того, это кольцо является полем, т.к. операция А 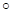В=АВ на этом множестве оказалась коммутативной (А 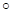В=В 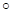А – убедиться самостоятельно ), нейтральным элементом относительно обычного умноженияявляется 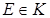, получается при х =0. И все ненулевые матрицы 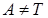9нулем данного кольца является матрица Т) будут невырожденными, а значит, обратимыми относительно обычного умножения матриц.

Можно проверить, что это кольцо К изоморфно кольцу R всех действительных чисел. При этом опять удобнее иметь дело не с матрицами, а с числами и операциями х Å у = х + у– 1, х _° у = х + у–ху. Изоморфизмом служит отображение j:(К, Å ,_°)® (R,+,_°), заданное формулой: j(х)=1–х. Действительно, это отображение – взаимно однозначно и сохраняет операции:

j(х Å у)=j(х+у– 1 )= 1 – (х+у– 1 )= 2 –х–у=( 1 –х)+( 1 –у)=j(х)+j (у);

j(х_° у)=j(х+у–ху)= 1 – (х+у-ху)= 1 –х–у–ху=( 1 –х)( 1 –у)=j(х)j(у).