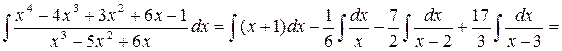Рациональной функцией или рациональной дробью называется функция следующего вида
 ,
,
где Qm (x) и Рn (х) — многочлены степени m и п соответственно. Если m<n, то дробь называется правильной, в противном случае – неправильной.
Любую неправильную дробь можно всегда преобразовать в сумму некоторого многочлена и правильной дроби, например, делением уголком.
Пример 6. Привести неправильную дробь к правильной дроби

Решение. Числитель данной дроби представим так: x+5=(x+1)+4. Далее

Дробь  является правильной (m=0, n=1)
является правильной (m=0, n=1)
Пример 7. Привести неправильную дробь к правильной дроби
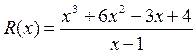
Решение. Числитель данной дроби разделим уголком на знаменатель:

Отсюда получаем следующее представление исходной функции через сумму квадратного многочлена и правильной функции:

Простейшими дробями называются дроби вида:

Дроби первого вида легко интегрируются непосредственно с помощью таблицы интегралов
Пример 8. Найти интеграл

Решение. 
Пример 9. Найти интеграл

Решение. 
Дроби второго вида в случае r=1 интегрируются так:
а) в числителе выделяется производная знаменателя
б) в знаменателе выделяется полный квадрат
В результате этих преобразований исходный интеграл распадается на два интеграла, которые достаточно легко сводятся к табличным интегралам
Пример 10. Найти интеграл

Решение. Сначала в числителе выделим производную знаменателя
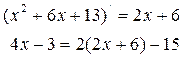
Получаем следующее представление исходного интеграла:

Первый интеграл в полученном выражении равен логарифму от модуля знаменателя, т.е.

В общем случае справедливо равенство:

В частности, если g (x)= x, то получаем табличный интеграл (см. п. 4)

Найдем второй интеграл. Для этого в знаменателе выделим полный квадрат:
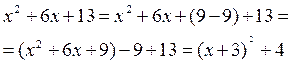
Второй интеграл в полученном выражении можно представить так:

Вычислим этот интеграл методом замены переменной
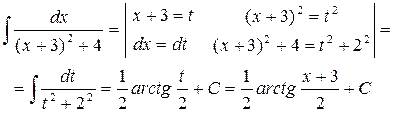
В общем случае справедливо равенство:

В частности, если a=1, то получаем табличный интеграл (см. п. 11)


Учитывая промежуточные результаты, окончательно получаем

Пример 11. Найти интеграл

Решение. По аналогии с предыдущим примером сначала в числителе выделим производную знаменателя

Получаем следующее представление исходного интеграла:

Первый интеграл в полученном выражении равен логарифму от модуля знаменателя, т.е.

Найдем второй интеграл. Для этого в знаменателе выделим полный квадрат:

Второй интеграл в полученном выражении можно представить так:

Вычислим этот интеграл методом замены переменной

В общем случае справедливо равенство:

В частности, если a=1, то получаем табличный интеграл (см. п. 13)

Учитывая промежуточные результаты, окончательно получаем

Дроби второго вида в случае r>1 интегрируются c помощью так называемых рекуррентных соотношений.
Итак, для вычисления интеграла от рациональной дроби

необходимо:
1) если функция неправильная, то преобразовать ее как правильную
2) разложить знаменатель на линейные или неприводимые квадратичные множители
в) записать правильную дробь в виде суммы простейших дробей с неопределенными коэффициентами
г) приводя сумму простейших дробей к общему знаменателю, получить систему линейных алгебраических уравнений относительно этих коэффициентов и решить ее
д) получить ответ с учетом вычисления интегралов от многочлена и простейших дробей
Пример 12. Вычислить интеграл:

Решение. Приводим заданную дробь к правильной дроби посредством деления многочленов уголком

Далее разложим знаменатель на линейные множители:

Теперь второе слагаемое можно представить так:

Полученную дробь можно разложить на сумму простейших дробей первого вида с неопределенными коэффициентами A, B, C:

Для отыскания этих коэффициентов найдем дополнительные множители:

Приравняем числители левой и правой частей:
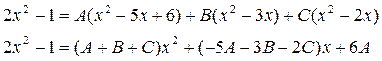
Из высшей алгебры известно, что многочлены равны, если все коэффициенты в них при соответствующих степенях между собой равны.
Приравняем коэффициенты при степенях x2, x, 1:
х2: А + В + С = 2
х1: 5А + 3В + 2С = 0
х0: 6А = - 1
Полученную систему решаем, например, по правилу Крамера. Для этого подсчитаем главный и три вспомогательных определителя.
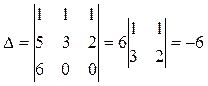



В соответствии с правилом Крамера имеем:

Итак, неопределенные коэффициенты определены. Подставляя вместо них конкретные численные значения, получаем