Группа 1БУ-67
Тема: Преобразование рациональных, иррациональных и степенных выражений.
Задание:
1. Изучить теоретические сведения и законспектировать их.
2. Записать примеры выполнения заданий.
3. Выполнить задания.
4. Выполненные задания сфотографировать и отправлять на электронную почту tryufelka83@mail.ru или в ЛС https://vk.com/tryufelka83 социальной сети VKontakte.
5. Выполненные задания сдать до: 26.10
Учебник: Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014.
Ссылка на учебник онлайн:
https://uchebnik-skachatj-besplatno.com/Алгебра/Учебник%20Алгебра%2010-11%20класс%20Алимов%20Колягин/index.html#prettyPhoto
С. 105-106
Повторим.
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.
Корень n – степени: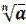 
, n - показатель корня, а – подкоренное выражение
Если n – нечетное число, то выражение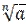 
имеет смысл при 
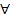а
Если n – четное число, то выражение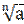 
имеет смысл при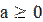 
Арифметический корень: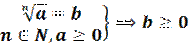 
Корень нечетной степени из отрицательного числа: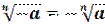 
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
1. Правило извлечения корня из произведения: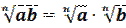 
2. Правило извлечения корня из дроби: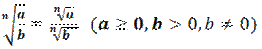 
3. Правило извлечения корня из корня: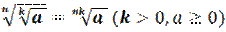 
4. Правило вынесения множителя из под знака корня: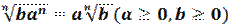 
5. Внесение множителя под знак корня:
,
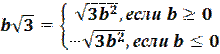6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.
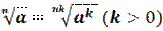
7. Правило возведения корня в степень.
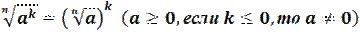
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
= 
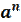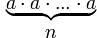, a – основание степени, n – показатель степени
Свойства:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
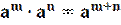
2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
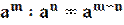
3. При возведении степени в степень показатели перемножаются.
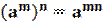
4. При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.
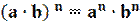
5. Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.
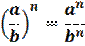
6. Если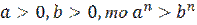 
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
1. 
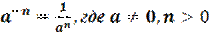
2. 
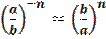
3. 
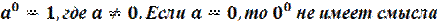
4. По определению: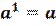 
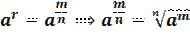
Свойства:
1. 
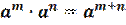
2. 
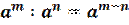
3. 
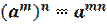
4. 
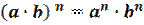
5. 
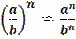
6. Пусть r рациональное число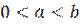 
, тогда
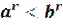при r>0 
> 
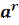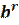при r<0
7. Для любого рациональных чисел r и s из неравенства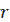 
> 
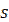следует
> 
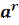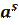при a>1 
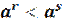при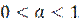 
Формулы сокращённого умножения.
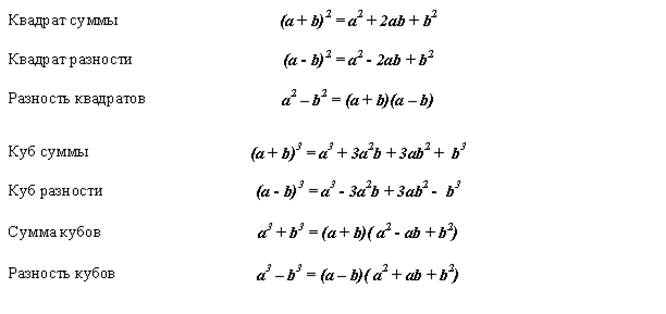
Пример. Упростите выражение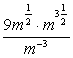 
.
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием):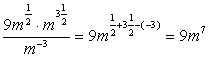 
.
Ответ: 9m7.
Пример. Сократить дробь: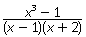 
Решение.Так область определения дроби 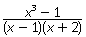все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем 
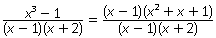.Сократив дробь, получим 
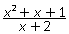.Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроб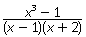и и 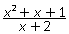равны при х ≠ 1 и х ≠ -2.
Пример. Сократить дробь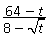 
, если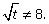 
Решение.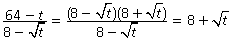 
.
Пример. Освободиться от иррациональности в знаменателе дроби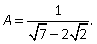 
Решение. В знаменателе имеем иррациональность 2-й степени, поэтому помножим и числитель, и знаменатель дроби на сопряженное выражение, то есть сумму чисел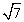 
и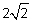 
, тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.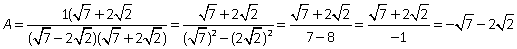 
Домашнее задание.
Выполнить пять заданий с. 37 «Проверь себя!»