ВАРИАЦИЯ ПРИЗНАКА И ПОКАЗАТЕЛИ ЕЕ ОЦЕНКИ

ТЕМА 4. ВАРИАЦИОННЫЙ АНАЛИЗ

Вариация признака и показатели ее оценки.

Дисперсия, ее свойства и методы расчета.

Виды дисперсии. Правило сложения дисперсий.

ВАРИАЦИЯ ПРИЗНАКА И ПОКАЗАТЕЛИ ЕЕ ОЦЕНКИ

Вариация – колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.

Рис. 1. Факторная классификация вариаций

Рис. 2. Классификация показателей вариации признака

 

Абсолютные показатели вариации – это размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и дисперсия.

Относительные показатели вариации – это коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Средняя арифметическая:

- для первичного ряда (простая средняя арифметическая):

;

- для ранжированного вариационного ряда (взвешенная средняя арифметическая):

.

Мода и медиана – структурные средние.

Мода – значение изучаемого признака, повторяющееся с наибольшей частотой.

Для интервального распределения с равными интервалами:

где

- нижняя граница модального интервала;

- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным.

 

Модальное значени е является валидной мерой центральной тенденции асимметричного распределения социально-экономических показателей.

 

Для интервального распределения с неравными интервалами:

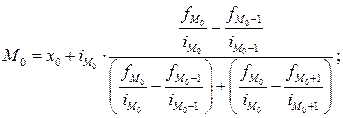
где

- начальная граница модального интервала, в котором достигает максимума величина - отношение частоты интервала к его величине;

- величина соответствующего модального, до- и послемодального интервалов;

- частота модального, до- и послемодального интервалов соответственно.

Медиана – значение признака, приходящееся на середину ранжированной совокупности. Структурные средние могут быть определены по дискретным и интервальным рядам распределения.

Формулы для исчисления медианы вариационного ряда:

- при нечетном числе вариантов - ;

- при четном числе вариантов - .

Формула для исчисления медианы интервального ряда:

где

- нижняя граница медианного интервала;

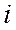- величина медианного интервала;

- накопленная частота интервала, предшествующего медианному;

- частота медианного интервала.

Размах вариации () – разность между наибольшим и наименьшим значениями варьирующего признака.

Среднее линейное отклонение – средняя арифметическая из абсолютных значений отклонений вариант признака от их средней. Эта величина вычисляется как средняя арифметическая из абсолютных значений отклонений вариант и :

простая -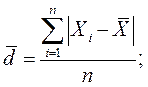

взвешенная –

Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины и в зависимости от исходных данных вычисляется по формулам:

- простой дисперсии –

- взвешенной дисперсии -

Среднее квадратическое отклонение (нормированное или стандартизированное отклонение) рассчитывается как корень квадратный из дисперсии. Оно может быть:

- простым -

- взвешенным -

Если распределение признака близко к нормальному или симметричному распределению, то или .

В условиях нормального распределения существует следующая взаимосвязь между величиной среднего квадратического отклонения 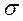и количеством наблюдений:

- в пределах располагается 68,3% количества наблюдений;

- в пределах располагается 95,4%;

- в пределах располагается 99,7% количества наблюдений.

Это положение называют правилом трех сигм.

Коэффициент осцилляции – процентное отношение размаха вариации к средней величине признака.

Линейный коэффициент вариации – процентное отношение среднего линейного отклонения к средней величине признака.

Коэффициент вариации – процентное отношение среднего квадратического отклонения к средней величине признака, т.е. это относительный показатель вариации признака.

В этой связи валидной мерой вариабельности асимметричного распределения социально-экономических показателей является среднее квадратическое отклонение.

Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие коэффициенты вариации.

Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанном с изменением вариант; кривую распределения применяют в качестве обобщающей характеристики особенностей формы распределения.

Нормальное распределение – это распределение, в котором средняя арифметическая, мода и медиана равны между собой. Формула функции плотности нормального распределения такова:

.

Следовательно, кривая нормального распределения может быть построена по двум параметрам – средней арифметической и среднему квадратическому отклонению .

Эмпирическая кривая распределения – это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение.

Теоретическая кривая распределения – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающем влияние случайных факторов.

Коэффициент асимметрии (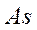) равен отношению центрального момента третьего порядка () к среднему квадратическому отклонению в кубе:

.

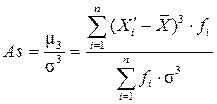Оценка существенности проводится на основе средней квадратической ошибки, коэффициента асимметрии , которая зависит от числа наблюдений () и рассчитывается по формуле: .

Если асимметрия существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна и ее наличие может быть вызвано случайными обстоятельствами. Распределение показателя с правосторонней асимметрией приводится к симметричному путем обратного преобразования показателя.

Для симметричных распределений с использованием центрального момент четвертого порядка () может быть рассчитан показатель эксцесса (), который определяют по формуле:

Рис.5. Островершинное (, а)) и плосковершинное (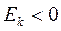, б)) распределения

 

Среднеквадратическая ошибка эксцесса () рассчитывается по формуле:

где - число наблюдений.

Для аппроксимации (выравнивания) эмпирических кривых распределения и сопоставления их с теоретическими в статистике часто пользуются нормальным распределением, функция которого имеет вид:

где - ордината кривой нормального распределения;

- стандартное отклонение;

- варианты вариационного ряда;

- их средняя величина;

- среднее квадратическое отклонение.

 

 

Плотность вероятности находится по формуле:

В математической статистике существуют специальные таблицы для любых значений . На основании полученных значений можно найти частоты нормального распределения ():

.

Критерии согласия – особые статистические показатели, характеризующие соответствие эмпирического и теоретического распределений. Критерий согласия Пирсона () вычисляется по формуле: где и - эмпирические и теоретические частоты соответственно.

В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место в ранжировано вариационном ряду.

Квартили – значения признака, делящие ранжированную совокупность на четыре равновеликие части нижний квартиль () отделяет часть совокупности с наименьшим значением признака; верхний квартиль () отсекает часть с наибольшими значениями признака.

Децили – значение признака, делящие ранжированную совокупность на десять равных частей.

Перцентили – значения признака, делящие ранжированную совокупность на сто равных частей.

Показатели дифференциации. По первичным данным может быть рассчитан коэффициент фондовой дифференциации, который представляет собой соотношение двух средних, полученных из 10% наибольших и наименьших значений признака:

.

Если представлены сгруппированные данные, то для характеристики дифференциации можно воспользоваться соотношением девятой и первой децили, которое характеризует коэффициент децильной дифференциации:

.

(децили делят все число единиц в совокупности на десять равных частей). Для определения децилей используются формулы аналогичные формулам расчета квартилей.

Децильный коэффициент дифференциации доходов населения (К_D), показывающий, во сколько раз минимальные дохо­ды 10% самого богатого населения превышают макси­мальные доходы 10% наименее обеспеченного населения:

,

где D₉, D₁ – девятый (самые высокие доходы) и первый (самые низкие доходы) дециль соответственно. Дециль – вариант ранжированного ряда, отсекающий десятую часть совокупности.

,

.

 

 

Рис. 4.12. Кривая Лоренца концентрации доходов населения

Коэффициент концентрации доходов (коэффициент Джини), характери­зующий степень неравенства в распределении доходов населе­ния, определяется по формуле:

где х_i — доля населения, принадлежащая к i-той социальной группе в общей численности населения;

y_i — доля доходов, сосредоточеннаяу i-той социальной груп­пы населения;

n — число социальных групп;

cum y_i — кумулятивная (исчисленная нарастающим итогом) доля дохода.

Коэффициент Джини изменяется в пределах от 0 до 1. При равномерном распределении этот коэффициент стремит­ся к нулю, а чем выше поляризация доходов в обществе, тем он ближе к единице.