ТЕЛА ВРАЩЕНИЯ
Цилиндр
 Пусть в плоскости α лежит некоторая линия PQ, и прямая MN пересекает эту плоскость. Если через каждую точку линии PQ провести прямые, параллельные прямой MN, то множество всех этих прямых образует поверхность, которая называется цилиндрической поверхностью. Цилиндрическую поверхность можно рассматривать как поверхность, которая образуется в результате движения прямой AB, остающейся при этом параллельной данной прямой MN и пересекающей линию PQ. Движущаяся прямая AB называется образующей цилиндрической поверхности, а линия PQ – её направляющей. Если направляющая – окружность, а образующая перпендикулярна плоскости α, то цилиндрическая поверхность называется прямой круговой.
Пусть в плоскости α лежит некоторая линия PQ, и прямая MN пересекает эту плоскость. Если через каждую точку линии PQ провести прямые, параллельные прямой MN, то множество всех этих прямых образует поверхность, которая называется цилиндрической поверхностью. Цилиндрическую поверхность можно рассматривать как поверхность, которая образуется в результате движения прямой AB, остающейся при этом параллельной данной прямой MN и пересекающей линию PQ. Движущаяся прямая AB называется образующей цилиндрической поверхности, а линия PQ – её направляющей. Если направляющая – окружность, а образующая перпендикулярна плоскости α, то цилиндрическая поверхность называется прямой круговой.
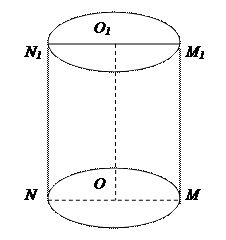 Тело, ограниченное прямой круговой цилиндрической поверхностью и двумя плоскостями, перпендикулярными образующей, называется прямым круговым цилиндром. Части секущих плоскостей, отсекаемые цилиндрической поверхностью, называются основаниями цилиндра. Часть цилиндрической поверхности, заключённая между основаниями, называется боковой поверхностью цилиндра. Расстояние между основаниями называется высотой.
Тело, ограниченное прямой круговой цилиндрической поверхностью и двумя плоскостями, перпендикулярными образующей, называется прямым круговым цилиндром. Части секущих плоскостей, отсекаемые цилиндрической поверхностью, называются основаниями цилиндра. Часть цилиндрической поверхности, заключённая между основаниями, называется боковой поверхностью цилиндра. Расстояние между основаниями называется высотой.
Прямая, проходящая через центры оснований цилиндра, называется его осью. Сечение цилиндра плоскостью, проходящей через ось, называется осевым. Цилиндр можно рассматривать как тело, образованное вращением прямоугольника MOO1M1 около оси.
Боковая поверхность цилиндра равна произведению длины окружности основания на высоту:  .
.
Объём цилиндра равен произведению площади его основания на высоту: 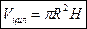 .
.
Конус
 Пусть в плоскости α лежит некоторая линия PQ. Возьмём вне этой плоскости точку S. Если через каждую точку линии PQ провести прямую, проходящую через точку S, то множество всех этих прямых образует поверхность, которая называется конической.
Пусть в плоскости α лежит некоторая линия PQ. Возьмём вне этой плоскости точку S. Если через каждую точку линии PQ провести прямую, проходящую через точку S, то множество всех этих прямых образует поверхность, которая называется конической.
Коническую поверхность можно рассматривать как поверхность, образующуюся в результате движения прямой SA, проходящей через неподвижную точку S и пересекающей при этом данную линию PQ.
Движущаяся прямая SA называется образующей конической поверхности, а линия PQ – её направляющей; точка S называется вершиной конической поверхности.
Тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины и секущей плоскостью, называется конусом. Часть конической поверхности, расположенная между её вершиной и секущей плоскостью, называется боковой поверхностью конуса, а часть секущей плоскости, ограниченная линией её пересечения с конической поверхностью – основанием конуса. Перпендикуляр, опущенный из вершины на основание, называется высотой конуса.
 Конус называется прямым круговым, если основанием его является круг, а высота проходит через центр этого круга. Прямой круговой конус можно рассматривать как тело, образованное в результате вращения треугольника SOA вокруг катета SO как оси.
Конус называется прямым круговым, если основанием его является круг, а высота проходит через центр этого круга. Прямой круговой конус можно рассматривать как тело, образованное в результате вращения треугольника SOA вокруг катета SO как оси.
Боковая поверхность конуса равна произведению длины окружности основания на половину образующей:  .
.
Объём конуса равен произведению площади его основания на треть высоты: 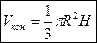 .
.
Усечённый конус
Определение. Часть конуса, заключённая между основанием и секущей плоскостью, параллельной основанию, называется усечённым конусом.
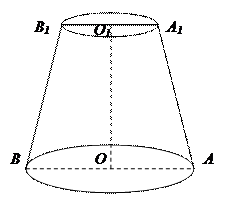 Круги OAB и O1A1B1 называются соответственно нижним и верхним основаниями конуса. Расстояние между плоскостями оснований называется высотой конуса. Часть образующей полного конуса, заключённая между основаниями усечённого конуса, называется его образующей.
Круги OAB и O1A1B1 называются соответственно нижним и верхним основаниями конуса. Расстояние между плоскостями оснований называется высотой конуса. Часть образующей полного конуса, заключённая между основаниями усечённого конуса, называется его образующей.
Усечённый конус может быть образован вращением прямоугольной трапеции OO1A1A вокруг оси OO1. При этом образующая описывает боковую поверхность усечённого конуса.
Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей основания на образующую: 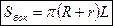 .
.
Объём усечённого конуса вычисляется по формуле: 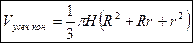 .
.
Шар
Определение. Тело, образованное вращением полукруга вокруг своего диаметра, называется шаром, а поверхность, образованная полуокружностью при этом вращении, - шаровой или сферической (сферой).
Шаровая поверхность (сфера) – это множество всех точек пространства, удалённых от данной точки O, называемой центром шаровой поверхности, на данной расстояние R, называемое радиусом.
Сфера определена, если известно положение её центра и длина радиуса. Отрезок, соединяющий две точки сферы, называется хордой. Хорда, проходящая через центр сферы, называется диаметром.
Два шара равны, если равны их радиусы, так как при вложении их можно совместить всеми точками.
Теорема 1. Всякое сечение шара плоскостью есть круг.
Если секущая плоскость проходит через центр шара, то все точки линии пересечения отстоят от точки O на расстоянии R, т.е. в этом случае в сечении получается круг, радиус которого равен радиусу шара. Такой круг называется большим кругом шара.
Следствие 1. Два сечения шара плоскостями, равноудалёнными от центра, равны между собой.
Следствие 2. Из двух сечений, неодинаково удалённых от центра, больше то, которое ближе расположено к центру.
Теорема 2. Через всякие две точки шаровой поверхности, не лежащие на концах одного диаметра, можно провести окружность большого круга и притом только одну.
Касательная плоскость.
Определение. Плоскость, имеющая с шаровой поверхностью только одну общую точку, называется касательной плоскостью.
Теорема. Плоскость, перпендикулярная радиусу, в конце его, лежащем на поверхности шара, есть касательная плоскость.
Справедлива обратная теорема: радиус, проведённый в точку касания, перпендикулярен касательной плоскости.
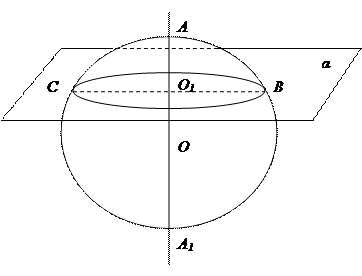 Поверхность шара и его частей.
Поверхность шара и его частей.
Площадь поверхности шара вычисляется по формуле:  .
.
Определение. Часть шаровой поверхности, отсечённая какой-либо плоскостью, называется сегментной поверхностью. Часть шаровой поверхности, заключённая между двумя секущими параллельными плоскостями, называется шаровым поясом.
Площадь сегментной поверхности равна 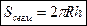 , где h – высота сегментной поверхности.
, где h – высота сегментной поверхности.
 Площадь поверхности шарового пояса равна
Площадь поверхности шарового пояса равна 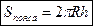 , где h – высота шарового пояса.
, где h – высота шарового пояса.
Объём шара и его частей.
Объём шара равен произведению его поверхности на одну треть радиуса:  .
.
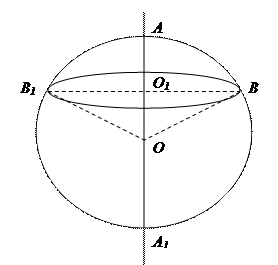
Шаровым сегментом называется часть плоскости, отсекаемая от него какой-либо плоскостью; его можно рассматривать как тело, полученное вращением кругового сегмента BAC вокруг его высоты AO1.
Шаровым сектором называется часть шара, полученная в результате вращения кругового сектора OAB вокруг крайнего радиуса OA.
Объём шарового сегмента равен 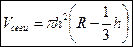 . В данной формуле R - радиус шара, h - высота сегмента.
. В данной формуле R - радиус шара, h - высота сегмента.
Объём шарового сектора вычисляется по формуле 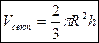 . Объём шарового сектора рассматривается как сумма объёмов шарового сегмента с высотой h и конуса с высотой R - h, где R – радиус шара.
. Объём шарового сектора рассматривается как сумма объёмов шарового сегмента с высотой h и конуса с высотой R - h, где R – радиус шара.
Задачи.
1. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
2. Цилиндр образован вращением прямоугольника вокруг одной из его сторон. Выразите объём V цилиндра через площадь S этого прямоугольника и длину C окружности, описанной точкой пересечения его диагоналей.
3. В цилиндре площадь сечения, перпендикулярного образующей, равна M, а площадь осевого сечения равна N. Определите полную поверхность и объём цилиндра.
4. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
5. Образующая конуса равна 6 см, а угол между нею и плоскостью основания равен 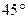 . Найдите объём конуса.
. Найдите объём конуса.
1) 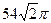 2)
2) 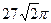 3)
3) 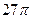 4)
4) 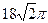 5)
5) 
6. Осевым сечением конуса является треугольник со сторонами 14 см, 25 см и 25 см. Найдите объём конуса.
1) 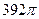 2)
2) 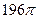 3)
3) 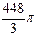 4)
4) 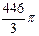 5)
5) 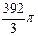
7. Образующая конуса равна 4 см, а угол при вершине осевого сечения равен 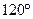 . Найдите объём конуса.
. Найдите объём конуса.
1) 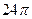 2)
2) 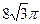 3)
3) 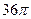 4)
4) 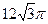 5)
5) 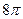
8. Осевое сечение конуса – прямоугольный треугольник с гипотенузой, равной 18 см. Найдите объём конуса.
1) 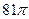 2)
2)  3)
3) 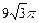 4)
4) 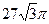 5)
5) 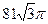
9. Осевое сечение конуса – равнобедренный треугольник с основанием 6 см. Образующая конуса наклонена к плоскости его основания под углом 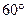 . Найдите объём конуса.
. Найдите объём конуса.
1) 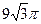 2)
2) 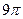 3)
3) 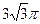 4)
4) 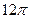 5)
5) 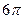
10. Радиус основания конуса равен R, а угол при вершине в развёртке его боковой поверхности равен 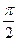 . Определите объём конуса.
. Определите объём конуса.
11. Боковая поверхность конуса развёрнута на плоскости в сектор, центральный угол которого содержит 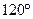 , а его площадь равна S. Найдите объём конуса.
, а его площадь равна S. Найдите объём конуса.
12. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
13. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
14. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
15. В конус, осевое сечение которого есть равносторонний треугольник, вписан шар. Найдите объём конуса, если объём шара равен 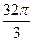 см3.
см3.
16. В шар вписан конус, образующая которого равна диаметру основания. Найдите отношение полной поверхности конуса к поверхности шара.
17. Металлический шар радиуса R перелит в конус, боковая поверхность которого в три раза больше площади его основания. Найдите высоту конуса.
18. У конуса и полушара общее основание с радиусом, равным R. Найдите площадь боковой поверхности конуса, если его объём равен объёму полушара.
19. Если сфера проходит через все вершины прямоугольного параллелепипеда с ребрами 1 см, 2 см и 2 см, то объём шара, ограниченного этой сферой, равен
1) 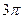 2)
2) 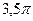 3)
3) 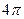 4)
4) 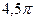 5)
5) 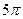
20. Даны шар, цилиндр с квадратным осевым сечением и конус. Цилиндр и конус имеют одинаковые основания, а их высоты равны диаметру шара. Как относятся объёмы цилиндра, шара и конуса?
21. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 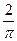 . Найдите объем цилиндра, описанного около этой призмы.
. Найдите объем цилиндра, описанного около этой призмы.
22. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
23. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен 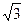 , а высота равна 2.
, а высота равна 2.
24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен 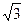 , а высота равна 2.
, а высота равна 2.
25. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
26. Треугольник со сторонами 10, 17 и 21 см вращается вокруг большей стороны. Вычислите объём и полную поверхность полученной фигуры вращения.
27. Равнобедренная трапеция с основаниями 2 и 3 см и острым углом 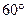 вращается вокруг меньшего основания. Вычислите площадь поверхности и объём полученной фигуры вращения.
вращается вокруг меньшего основания. Вычислите площадь поверхности и объём полученной фигуры вращения.