Теорема Чебышева. Пусть дисперсии независимых СВ Х1,Х2,…,Хn ограничены одной и той же постоянной С, а число их достаточно велико. Тогда, как бы мало не было число ε >0,вероятность того, что отклонение среднего арифметического этих СВ от среднего арифметического их математических ожиданий не превзойдет ε по абсолютной величине, сколь угодно близка к единице.
Следствие. Если независимые СВ имеют одинаковые математические ожидания, равные а, дисперсии их ограничены одной и той же постоянной С, а число их достаточно велико, то для любого ε >0 вероятность того, что отклонение среднего арифметического этих СВ от а не превзойдет по абсолютной величине ε,сколь угодно близка к единице:
Р (| Х1+Х2+…Хn / n –а |≤ ε)>1- 
, как бы ни были малы ε и .Следствие 1 является наиболее простой формой закона больших чисел. Согласно закону больших чисел, среднее арифметическое достаточно большого числа измерений практически будет, как угодно мало отличаться от истинного значения математического ожидания искомой величины.
24. Закон больших чисел. Теорема Пуассона и Теорема Бернулли.
Закон больших чисел — поведение случайных величин так что, при некоторых условиях суммарное поведение достаточно большого числа СВ почти утрачивает случайный характер и становится закономерным.
Т. Бернулли Пусть производится n независимых испытаний, в каждом из которых вероятность появления события постоянна и равна р. Тогда каково бы ни было ε > 0,
где m/n - частость (относитетельная частота) появления события А.
Следствие (теорема Пуассона). Если вероятность pi наступления события А в i-испытании (i= 
) не меняется, когда становятся известными исходы предыдущих испытаний, а число испытаний n достаточно велико, то вероятность того, что частность события А будет как угодно мало отличаться от среднего арифметического вероятностей pi, сколь угодно близка к единице:
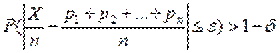, для любых ε >0 и 
>0
Т. Пуассона
Если в последовательности независимых испытаний появление события А в k-ом испытании равна рk, то
где m есть случайная величина, равная числу появлений события А в первых n испытаниях.
Следствие (теорема Бернулли). Если вероятность р наступления события А в каждом из n независимых испытаний постоянна, а число испытаний достаточно велико, то вероятность того, что частость события А будет как угодно мало отличаться от его вероятности, сколь угодно близка к единице:
25. Центральная предельная теорема. Теорема Ляпунова.
Центральные предельные теоремы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному
Теорема Ляпунова. Рассмотрим n независимых случайных величин Х1, Х2,…,Хn, удовлетворяющих условиям:
1) все величины имеют определенные математические ожидания и конечные дисперсии;
2) ни одна из величин не выделяется резко от остальных по своим значениям.
Тогда при неограниченном возрастании n распределение случайной величины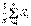 
приближается к нормальному закону.
Таким образом, имеем следующую асимптотическую формулу:
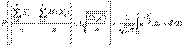
где 
.