Свободные колебания
Курсовая работа по программированию
и информатике.
Выпонила студентка 204 группы
Е. М. Мухоян
Преподаватель
А. А. Лукашёв
Москва – 2017
Аннотация
В курсовой работе рассмотрена задача о свободных негармонических колебаниях математического маятника.
Показано:
1) при малой амплитуде координата и скорость зависят от времени движения по гармоническому закону, фазовый портрет системы имеет форму эллипса
2) с увеличением амплитуды колебания перестают быть гармоническими, фазовый портрет теряет форму эллипса
3) в случае негармонических колебаний частота колебаний зависит от их амплитуды
Содержание
Введение.
Физическая постановка задачи ………………………………………………………………… 4
Анализ основных уравнений
Основное уравнение движения………………………………………………………………...…. 4
Описание метода моделирования
3.1 Выбор численного метода…………………………………………………………………….. 4
3.2 Метод Рунге-Кутта…………………….………………………………………………………. 4
Результаты численных расчётов
Обработка полученных данных……………………………………………................................... 5
5 Выводы … ……… ………………………. ……………………
..……….………………………..... 9
Введение.
Физическая постановка задачи
Задача о колебании математического маятника. Математический маятник – это осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения [1].
Анализ основных уравнений
Основное уравнение движения
Основное уравнение движения – второй закон Ньютона [2], который записывается в виде:
 . (1)
. (1)
Описание метода моделирования
Выбор численного метода
Для численного решения поставленной задачи наилучшим оказывается применение метода Рунге-Кутта 4-го порядка. Потому что метод 4-го порядка имеет преимущество перед методами 1-го и 2-го порядков, так как он обеспечивает малую локальную ошибку. Это позволяет увеличить шаг интегрирования и, следовательно, сократить время расчета [3].
Метод Рунге-Кутта
Для численного решения поставленной задачи применялся метода Рунге-Кутта 4-го порядка. Метод Рунге-Кутта – это класс численных методов для решения задачи Коши для дифференциальных уравнений и их систем [4]. Первые методы данного класса были предложены около 1900 года немецкими математиками К. Рунге и М. В. Куттой [5]. В данной задаче применяется метод Рунге-Кутта 4-го порядка при вычислениях с постоянным шагом интегрирования. Этот метод имеет четвёртый порядок точности.
В нашем случае численная схема выглядит следующим образом:
 ,
,
(2)
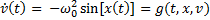 ,
,
где
 ,
,
(3)
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
(4)
 ,
,
 ,
,
 ,
,
 .
.
Результаты численных расчётов
Обработка полученных данных
В результате проведения численного эксперимента были получены несколько серий, анализ которых показывает:
1. Зависимости координаты и скорости от времени периодические (см. Рис.1, Рис.3, Рис.5 и Рис.7);
2. При малой амплитуде (при малом угле отклонения маятника от положения равновесия) колебания системы близки к гармоническим (см. Рис.1, Рис.3 и Рис.5), и с увеличением амплитуды (угла отклонения) перестают быть гармоническими (см. Рис.7);
3. При гармонических колебаниях фазовый портрет системы имеет форму эллипса (см. Рис.2, Рис.4 и Рис.6), и теряет форму эллипса, когда колебания перестают быть гармоническими (см. Рис.8);
4. В условии негармонических колебаний частота колебаний уменьшается с ростом амплитуды (см. Рис.1, Рис.3, Рис.5, Рис.7 и Рис.9).

Рис. 1. Зависимости координаты и скорости от времени при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),  (рад./c.).
(рад./c.).

Рис.2. Зависимость скорости от координаты при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),
 (рад./c.).
(рад./c.).

Рис.3. Зависимости координаты и скорости от времени при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),  (рад./c.).
(рад./c.).

Рис.4. Зависимость скорости от координаты при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),
 (рад./c.).
(рад./c.).

Рис.5 Зависимости координаты и скорости от времени при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),  (рад./c.).
(рад./c.).

Рис.6. Зависимость скорости от координаты при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),
 (рад./c.).
(рад./c.).

Рис.7. Зависимости координаты и скорости от времени при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),  (рад./c.).
(рад./c.).

Рис.8. Зависимость скорости от координаты при  (отн. ед.),
(отн. ед.),  (отн. ед.),
(отн. ед.),
 (рад./c.).
(рад./c.).

Рис.9. Зависимость частоты колебаний от амплитуды.
Выводы
По результатам проделанной работы можно сделать следующие выводы:
· Колебания математического маятника при данных условиях – это свободные незатухающие колебания, которые при малой амплитуде являются гармоническими.
· При малой амплитуде колебаний координата и скорость зависят от времени по гармоническому закону, фазовый портрет системы имеет форму эллипса.
· С увеличением амплитуды колебания перестают быть гармоническими, фазовый портрет теряет форму эллипса.
· В случае негармонических колебаний частота колебаний уменьшается с увеличением их амплитуды.
Список литературы
1. А. Н. Матвеев «Механика и теория относительности» 1-ое изд. М.: Высшая школа, 1976.
2. Д. В. Сивухин «ОБЩИЙ КУРС ФИЗИКИ. Том 1. МЕХАНИКА» М.: Наука, 1979.
3. Б. П. Демидович, И. А. Марон, Э. З. Шувалова «Численные методы анализа» 3-е изд. М.: Наука, 1967.
4. Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков «Численные методы» М.: Лаборатория Базовых Знаний, 2001.
5. В. А Ильина, П. К. Силаев «Численные методы для физиков-теоретиков Ч. 2» Москва-Ижевск: Институт компьютерных исследований, 2004.