Автоматическое доказательство теорем является основой логического программирования, одним из способов построения систем искусственного интеллекта.
Алгоритм, который проверяет соотношение G |-T S для формулы S, множества формул G и теории T называется алгоритмом автоматического доказательства теорем.
Для достаточно простых формальных теорий, например, прикладных исчислений первого порядка такой алгоритм существует. Автоматическое доказательство проводится методом резолюций, в основе которого лежит способ доказательства от противного. Часто логическим программированием называют автоматическое доказательство методом резолюций, однако этот метод лишь наиболее разработанный его частный случай.
Теорема 7.1. Если G, Ø S |- F, где F – любое противоречие, то G |- S.
Доказательство. Если G, Ø S |- F, то GÙ(Ø S)|- F, так как GÙ(Ø S)|- G и GÙ(Ø S)|- Ø S. Следовательно, |- GÙ(Ø S) ® F. Так как
GÙ(Ø S) ® F º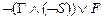 
º 
º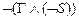 
º 
,
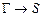то |- 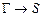и, следовательно, G |- S.
Метод резолюций работает со стандартной формой формул, называемой предложениями. Предложением называется бескванторная дизъюнкция литералов. Любая формула исчисления предикатов может быть преобразована в множество предложений по следующему алгоритму.
1. Построить предварённую нормальную форму формулы. Напомним, что для этого нужно:
a) преобразовать формулу к приведённому виду, т.е. исключить операцию ® и спустить операцию отрицания до атомарных формул;
b) провести разделение связанных переменных;
c) вынести операции связывания переменных в начало формулы.
2. Преобразовать предварённую нормальную форму в предклазуальную, т.е. привести матрицу U нормальной формы к КНФ.
3. Провести сколемизацию нормальной формы (построить клазуальную нормальную форму, исключив операции связывания переменных).
4. Удалить операции Ù (дизъюнкции клазуальной нормальной формы составят искомое множество предложений).
Далее к предложениям, полученным из формул множества G и из формулы Ø S, применяется правило резолюции. Сформулируем это правило для исчисления высказываний, а, затем, обобщим его для исчисления предикатов.
Определение. Пусть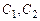 
– предложения исчисления высказываний, такие что 
, 
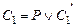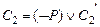. Правило вывода
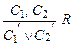
называется правилом резолюции исчисления высказываний, предложения 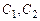– резольвируемыми, а 
– резольвентой.
Замечание. Многие рассмотренные ранее правила вывода являются частными случаями правила резолюции. Например, основное правило исчисления ИВ – правило заключения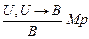 
можно представить в виде 
.
Таким образом, множество предложений будет являться противоречивым, если в результате последовательного применения правила резолюции, получим пустую формулу, которую будем обозначать š. Действительно, если резольвента пуста, то резольвируемые предложения – взаимно противоположные высказывания и система предложений противоречива.
Задание 1. Доказать методом резолюций |-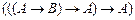 
.
Решение. В данном примере G – пусто,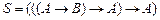 
. Преобразуем формулу 
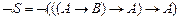в множество предложений.
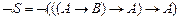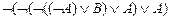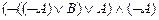º 
º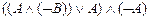
º 
º 
º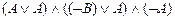
º 
º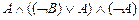 
1. A
2. 
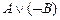
3. Ø A
4. š
Применив к предложениям 1, 3 правило резолюции, получим пустую формулу, то есть противоречие. Следовательно, формула S является выводимой из пустого множества посылок или теоремой рассматриваемой теории.
Для того чтобы сформулировать правило резолюции для исчисления предикатов введём понятие унификатора.
Определение. Подстановкой q сигнатуры s называется конечное множество вида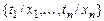 
, где 
– терм сигнатуры s, отличный от переменных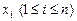 
и все переменные 
различны.
Например, множества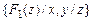 
и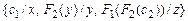 
являются подстановками сигнатуры 
.
Пусть U – формула, а q – подстановка сигнатуры s. Обозначим через 
формулу, полученную заменой всех вхождений 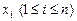на термы .
Определение. Подстановка q сигнатуры s называется унификатором для множества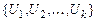 
формул сигнатуры s, если 
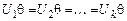. Множество формул 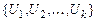сигнатуры s, называется унифицируемым, если для него существует унификатор сигнатуры s.
Например, множество формул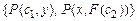 
сигнатуры 
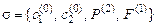унифицируемо, так как подстановка 
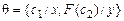является его унификатором.
Определение. Пусть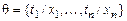 
и 
– подстановки сигнатуры s. Композицией подстановок q и l (обозначается q ° l) называется подстановка, которая получается из множества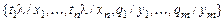 
вычеркиванием всех элементов 
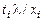, для которых 
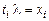, и всех элементов 
, для которых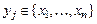 
.
Пример. Пусть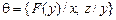 
, 
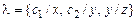. Тогда = 
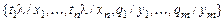, а так как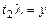 
и 
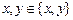, то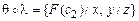 
.
Определение. Унификатор t для множества 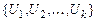формул сигнатуры s называется наиболее общим унификатором (НОУ), если для каждого унификатора q сигнатуры s этого множества существует подстановка l сигнатуры s такая, что 
.
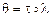Так для множества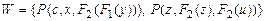 
наиболее общим унификатором является подстановка 
.
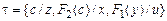Определение. Пусть 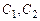– предложения исчисления предикатов, такие что 
, 
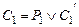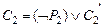, а атомарные формулы 
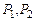унифицируемы наиболее общим унификатором t. Правило вывода
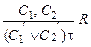
называется правилом резолюции исчисления предикатов.
Задание 2. Проверить G |-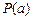 
, где
G: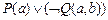 
, 
, 
, 
.
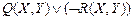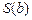Решение. Выпишем множество предложений G, Ø S, пронумеровав их.
1.
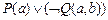
2.
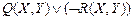
3.
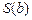
4.
5. 
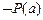
Далее будем добавлять предложения в это множество, применяя правило резолюции с возможной предварительной унификацией. Рядом с новым предложением будем указывать способ его получения (правило резолюции или унификация) и номера предложений, к которым он применялся.
6. 
R (1, 5)
7. 
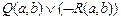
(2, 6)
8. 
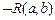R (6, 7)
9. 
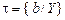(4, 8)
10. š R (8, 9)
Следовательно, G |- .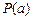
Работа метода резолюций может иметь следующие варианты результатов:
1) на очередном шаге получено пустое предложение и, следовательно, формула S является следствием G (теорема 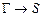доказана);
2) если во множестве предложений нет новых резольвируемых предложений, то теорема опровергнута;
3) множество предложений постоянно пополняется новыми предложениями (зацикливание), что означает, что средств данной теории недостаточно ни для того, чтобы доказать теорему, ни для того, чтобы её опровергнуть.
Представим алгоритм работы метода резолюций на языке описания алгоритмов. Результат 1 – если S выводимо из G, 0 – в противном случае. Обозначим M – множество предложений, C – множество предложений, полученное из G и Ø S. Функция choose выполняет выбор резольвируемых предложений, R – вычисляет резольвенту.
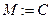
while ÿÏ C
begin choose (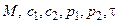
)
if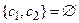 
then return 0
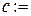R(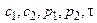
)
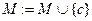
end
return 1