Правила записи приближенных чисел.

1. Приближенные числа записываются в форме х ± Dх. Запись X = х ± Dx означает, что неизвестная величина X удовлетворяет следующим неравенствам: x-Dx <= X <= x+Dx

При этом погрешность Dх рекомендуется подбирать так, чтобы

а) в записи Dх было не более 1-2 значащих цифр;

б) младшие разряды в записи чисел х и Dх соответствовали друг другу.

Примеры: 23,4±0,2; 2,730±0,017; -6,97±0,10.

2. Приближенное число может быть записано без явного указания его предельной абсолютной погрешности. В этом случае в его записи (мантиссе) должны при­сутствовать только верные цифры (в широком смысле, если не сказано обратное). Тогда по самой записи числа можно судить о его точности.

Примеры. Если в числе А=5,83 все цифры верны в строгом смысле, то DА=0,005. Запись В=3,2 подразумевает, что DВ=0,1. А по записи С=3,200 мы можем заключить, что DС=0,001. Таким образом, записи 3,2 и 3,200 в теории приближенных вычислений означают не одно и то же.

Цифры в записи приближенного числа, о которых нам неизвестно, верны они или нет, называются сомнительными. Сомнительные цифры (одну-две) оставляют в за­писи чисел промежуточных результатов для сохранения точности вычислений. В окончательном результате сомнительные цифры отбрасываются.

Округление чисел.

1. Правило округления. Если в старшем из отбрасываемых разрядов стоит цифра меньше пяти, то содержимое сохраняемых разрядов числа не изменяется. В проти­вном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа.

2. При округлении числа, записанного в форме х±Dх, его предельная абсолютная погрешность увеличивается с учетом погрешности округления.

Пример: Округлим до сотых число 4,5371±0,0482. Неправильно было бы записать 4,54±0,05, так как погрешность округленного числа складывается из погрешности исходного числа и погрешности округления. В данном слу­чае она равна 0,0482 + 0,0029 = 0,0511. Округлять погрешности все­гда следует с избытком, поэтому окончательный ответ: 4,54±0,06.

 

Пример Пусть вприближенном значении а = 16,395 все циф­ры верны в широком смысле. Округлим а до сотых: a ₁= 16,40. Погрешность округления Для нахождения полной погрешности 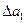,нужно сложить c погрешностью исходного значения а₁ которая в данном случае может быть найдена из условия, что все цифры в записи а верны: 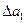= 0,001. Таким образом, . Отсюда следует, что взначении a ₁ = 16,40 цифра 0 не верна в строгом смысле.

3. Вычисление погрешностей арифметических действий

1. Сложение и вычитание. Предельной абсолютной погрешностью алгебраической суммы является сумма со­ответствующих погрешностей слагаемых:

Ф.1 D(X+Y) = DХ + DY, D(X-Y) = DХ + DY.

Пример. Даны приближенные числа Х = 34,38 и Y = 15,23, все цифры верны в строгом смысле. Найти D(X-Y) и d(X-Y). По формуле Ф.1 получаем:

D(X-Y) = 0,005 + 0,005 = 0,01.

Относительную погрешность получим по формуле связи:

 

2. Умножение и деление. Если dХ << |Х| и dY << |Y|, то имеет место следующая формула:

Ф.2 d(X · Y) = d(X/Y) = dX + dY.

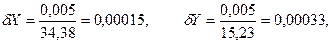Пример. Найти D(X·Y) и d(X·Y) для чисел из предыдущего примера. Сначала с по­мощью формулы Ф.2 найдем d(X·Y):

d(X·Y)= dX + dY=0,00015+0,00033=0,00048

 

Теперь D(X·Y) найдем с помощью формулы связи:

D(X·Y) = |X·Y|·d(X·Y) = |34,38 -15,23|·0,00048 £ 0,26.

3. Возведение в степень и извлечение корня. Если dХ << |Х|, то справедливы формулы

Ф.З

4. Функция одной переменной.

Пусть даны аналитическая функция f(x) и приближенное число с ± Dс. Тогда, обозначая через D малое приращение аргумента, можно написать

 

Если f '(с) ¹ 0, то приращение функции f(с+D) - f(c) можно оценить ее диффе­ренциалом:

f(c+D) - f(c) » f '(c) ·D.

Если погрешность Dс достаточно мала, получаем окончательно следующую форму­лу:

Ф.4 Df(c) = |f '(с)|· Dс.

Пример. Даны f(x) = arcsin x, с = 0,5, Dс = 0,05. Вычислить Df(с).

Применим формулу Ф.4:

и т. д.

 

5. Функция нескольких переменных.

Для функции нескольких переменных f(x1,..., хn) при xk= ck ± Dck справед­лива формула, аналогичная Ф.4:

Ф.5 Df(c1,...,сn) » l df(c1,...,сn) | = |f 'x1 (с1)|·Dс1+... + |f 'xn (сn)|· Dсn.

Пример Пусть х = 1,5, причем т.е. все цифры в числе х верны в строгом смысле. Вычислим значение tg x. С помощью МК получаем: tgl,5= 14,10141994. Для определения верных цифр в результате оценим его абсолютную погрешность: 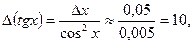отсюда следует, что в полученном значении tgl,5 ни одну цифру нельзя считать верной.

 

4. Методы оценки погрешности приближенных вычислений

Существуют строгие и нестрогие методы оценки точности результатов вычислений.

1. Строгий метод итоговой оценки. Если приближенные вычисления выполняются по сравнительно простой формуле, то с помощью формул Ф.1-Ф.5 и формул связи погрешностей можно вывести формулу итоговой погрешности вычислений. Вывод форму­лы и оценка погрешности вычислений с ее помощью составляют суть данного мето­да.

Пример Значения a = 23,1 и b = 5,24 даны цифрами, верными в строгом смысле. Вычислить значение выражения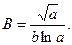

С помощью МК получаем В = 0,2921247. Используя формулы относительных погрешностей частного и произведения, запишем:

т.е.

Пользуясь МК, получим 5, что дает . Это означает, что в результате две цифры после запятой верны в строгом смысле: В=0,29±0,001.

2. Метод строгого пооперационного учета погрешностей. Иногда попытка примене­ния метода итоговой оценки приводит к слишком громоздкой формуле. В этом слу­чае более целесообразным может оказаться применение данного метода. Он заклю­чается в том, что оценивается точность каждой операции вычислений отдельно с помощью тех же формул Ф.1-Ф.5 и формул связи.

3. Метод подсчета верных цифр. Данный метод относится к нестрогим. Оценка точ­ности вычислений, которую он дает, в принципе не гарантирована (в отличие от строгих методов), но на практике является довольно надежной. Суть метода заключается в том, что после каждой операции вычислений в полученном числе определяется количество верных цифр с помощью нижеследующие правил.

П.1. При сложении и вычитании приближенных чисел в результате верными следует считать, те цифры, десятичным разрядам которых соответствуют верные цифры во всех слагаемых. Цифры всех других разрядов кроме самого старшего из них перед выполнением сложения или вычитания должны быть округлены во всех слагаемых.

П.2. При умножении и делении приближенных чисел в результате верными следует считать столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством верных значащих цифр. Перед выполнением этих действий среди приближенных данных нужно выбрать число с наименьшим количеством знача­щих цифр и округлить остальные числа так, чтобы они имели лишь на одну знача­щую цифру больше него.

П.З. При возведении в квадрат или в куб, а также при извлечении квадратного или кубического корня в результате следует считать верными столько значащих цифр, сколько имелось верных значащих цифр в исходном числе.

П.4. Количество верных цифр в результате вычисления функции зависит от величины модуля производной и от количества верных цифр в аргументе. Если модуль производной близок к числу 10k (k - целое), то в результате количество верных цифр относительно запятой на k меньше (если k отрицательно, то - больше), чем их было в аргументе. В данной лабораторной работе для определенности примем соглашение считать модуль, производной близким к 10k, если имеет место нера­венство:

0,2·10K < |f '(X) | £ 2·10k.

П.5. В промежуточных результатах помимо верных цифр следует оставлять одну сом­нительную цифру (остальные сомнительные цифры можно округлять) для сохранения точности вычислений. В окончательном результате оставляют только верные цифры.