Лекция 11
В переменном электромагнитном поле наблюдаются одновременно обе, рассмотренные ранее нами в отдельности, его стороны. Связь между ними дают первое и второе уравнения Максвелла – закон полного тока и закон электромагнитной индукции:
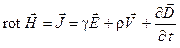 ,
, 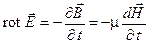 .
.
Анализируя переменное электромагнитное поле в диэлектрике, считаем диэлектрик идеальным (g=0) и предполагаем отсутствие в нем объемных зарядов (r=0). Тогда:
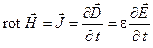
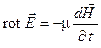
Запишем оба уравнения в проекциях на оси декартовой системы координат:
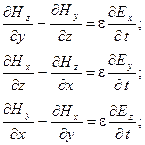
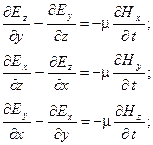
Рассмотрим случай плоско поляризованной электромагнитной волны, в которой все характеризующие ее величины зависят только от одной из координат (z), а от остальных координат (x, y) не зависят. Такой характер имеют электромагнитные волны, излучаемые антенной, на больших (z>>l) расстояниях от антенны, где l - длина электромагнитной волны в диэлектрике. Часто такую волну называют плоской.
В плоской электромагнитной волне производные от любых проекций векторов поля по координатам x и y равны нулю, поэтому система уравнений упрощается и принимает вид:
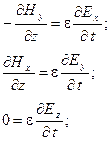
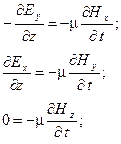
Из последних уравнений каждой системы ввиду равенства нулю производных получаем, что проекции векторов Ez и Hz не зависят от времени: Ez =const и Hz =const. Принимаем их равными нулю, так как переменное поле, излученное антенной, не содержит постоянных составляющих. Кроме того, мы уже рассматривали ранее постоянные электрические и магнитные поля, и в случае необходимости можем, если потребуется учесть их вместе с переменным полем, применив принцип наложения.
Рассматривая оставшиеся четыре уравнения для проекций, направим ось x декартовой системы координат вдоль вектора напряженности электрического поля (Ey =0). В этом случае остается единственная составляющая вектора напряженности электрического поля: E=Ex. В этом случае уравнения еще больше упрощаются:
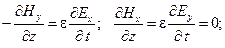

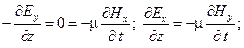
Из полученных уравнений следует, что 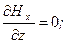

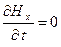 , т.е.
, т.е. 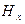 =const=0,
=const=0,
и при выбранном направлении осей координат, вектор напряженности магнитного поля имеет лишь единственную составляющую, направленную вдоль оси y: H=Hy. Это означает, что в плоско поляризованной электромагнитной волне в диэлектрике в любой точке векторы напряженности электрического и магнитного поля расположены взаимно перпендикулярно.
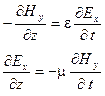 Найдем решение системы двух оставшихся уравнений:
Найдем решение системы двух оставшихся уравнений:
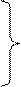
Дифференцируя первое уравнение по времени, а второе по координате z, получим:

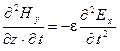 ;
; 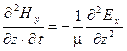 , откуда:
, откуда: 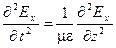 , и обозначив
, и обозначив 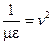 , запишем уравнение для вектора напряженности электрического поля, которое называется волновым уравнением:
, запишем уравнение для вектора напряженности электрического поля, которое называется волновым уравнением:
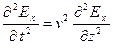
При рассмотрении режимов в цепях с распределенными параметрами нами были получены аналогичные уравнения для напряжения в произвольной точке линии без потерь, в которой координата x отсчитывается от начала линии:
 .
.
Решение для волнового уравнения в линии мы получили в виде суммы прямой и обратной бегущих волн напряжения:
 u = uj + uy = u/ (x-vt) + u// (x+vt).
u = uj + uy = u/ (x-vt) + u// (x+vt).
Решение для напряженности электрического поля запишем по аналогии:
Ex = E/ (z-vt) + E// (z+vt).
Коэффициенты 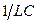 и
и 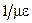 в обоих уравнениях имеют одинаковые размерности, так как в цепях с распределенными параметрами эти параметры задаются на единицу длины линии:
в обоих уравнениях имеют одинаковые размерности, так как в цепях с распределенными параметрами эти параметры задаются на единицу длины линии:
[ L ] = [m] = Гн/м; [ C ] = [e]= Ф/м
Выражение для волн тока в линии мы получали с помощью волнового сопротивления:
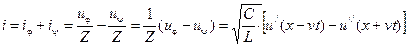 ,
,
здесь через Z обозначено волновое сопротивление линии без потерь, которое по аналогии эквивалентно волновому сопротивлению идеального диэлектрика для электромагнитных волн:
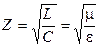 .
.
Применив аналогичное преобразование для решения волнового уравнения относительно напряженности электрического поля, получим решения для напряженности магнитного поля:
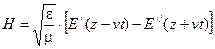 .
.
Полученные решения означают, что векторы E и H в любой точке переменного электромагнитного поля взаимно перпендикулярны, связаны между собой через волновое сопротивление, а электромагнитные волны распространяются в диэлектрике со скоростью v, которая называется скоростью света и в пустоте равна:
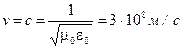
В любых диэлектриках e≥e0 и m≥m0, поэтому скорость распространения электромагнитных волн в них меньше или равна скорости света в пустоте v £ c.
Волновое сопротивление, связывающее между собой напряженности электрического и магнитного поля в прямой и обратной волнах:
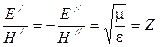 ,
,
также зависит от свойств диэлектрика и для пустоты равно:
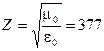 Ом
Ом
Для прямой (или обратной) волны в отдельности можем записать соотношение:
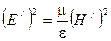 ;
; 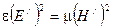 ;
; 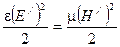 .
.
Это означает, что плотности энергии электрического и магнитного поля в любой точке для прямой (или обратной) электромагнитной волны равны друг другу:
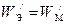 .
.
Для электромагнитных волн в идеальном диэлектрике можно использовать по аналогии все ранее полученные соотношения для бегущих волн в однородной линии без потерь. В частности, справедливы формулы для определения отраженной и преломленной волн на границе диэлектриков с различными волновыми сопротивлениями. При этом соблюдаются все граничные условия для составляющих векторов напряженности электрического и магнитного поля. Вообще, решение волнового уравнения может быть получено, если заданы граничные и начальные условия для векторов.
Вектор Умова-Пойнтинга.
Рассмотрим бесконечно малый объем dV в виде цилиндра, длиной dl, ось которого направлена вдоль оси z, совпадающей с направлением распространения электромагнитной волны (рис. 11–1).
 x
x
dV ds
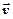
z 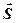
y
dl
Рисунок 11–1
В бесконечно малом объеме dV=dlds при наличии электромагнитной волны, движущейся только в одном направлении (прямой, либо обратной), запасена некоторая энергия, плотность которой в пределах бесконечно малого объема постоянна и равна:
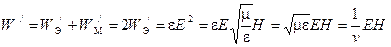 .
.
Энергия, запасенная в объеме dV, равна:
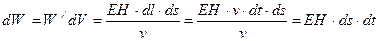 .
.
Так как электромагнитная волна движется вдоль оси z со скоростью v, то в том же направлении перемещается и связанная с ней энергия. Мощность потока электромагнитной энергии, проходящей сквозь площадку ds,определяется соотношением:
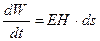 ,
,
а мощность потока электромагнитной энергии, отнесенная к единице поверхности, обозначается через S,и равна:
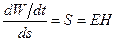
Мощность потока электромагнитной энергии через единицу поверхности может рассматриваться как вектор, направленный в сторону движения электромагнитной волны, вместе с которой перемещается и связанная с ней энергия. Этот вектор называется вектором Умова-Пойнтинга, и его направление связано с направлением векторов напряженности электрического и магнитного поля с помощью их векторного произведения:
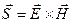
В прямой электромагнитной волне напряженность электрического и магнитного поля одного знака (Ex >0, Hy >0 или Ex <0, Hy <0) вектор скорости направлен вдоль оси z (Vz >0), и вектор Пойнтинга направлен в туже сторону (рис. 11–2а). В обратной электромагнитной волне напряженность электрического и магнитного поля разного знака (Ex >0, Hy <0 или Ex <0, Hy >0) вектор скорости направлен против оси z (Vz <0), и вектор Пойнтинга также направлен против оси z (рис. 11–2б).
 x
x  x
x
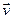
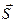
z z
y 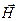 y
y 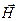
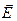
а) прямая волна б) обратная волна
Рисунок 11–2
Вектор Пойнтинга определяет мощность потока электромагнитной энергии сквозь единицу поверхности, перпендикулярной направлению движению волны, и совпадает с ним по направлению.
Рассмотрим в качестве примера переходные процессы при заряде (рис 11–3а) и разряде (рис 11–3б) плоского конденсатора.
Направление вектора плотности тока смещения совпадает с направлением приращения вектора смещения или вектора напряженности электрического поля:
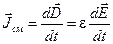
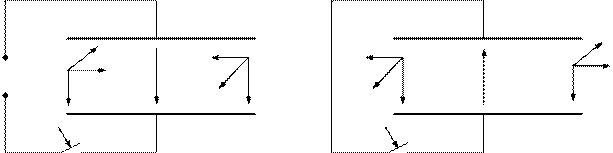
+ + + + + + + + + + + + + + + + + + + + + + + + + + + +
H S S H
+ S J см J см S
– E H E H E E
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
а) б)
Рисунок 11–3
При заряде (а) конденсатора напряженность электрического поля возрастает, и вектор плотности тока смещения направлен в ту же сторону, что и вектор напряженности электрического поля, а при разряде конденсатора поле ослабевает, и вектор плотности тока смещения направлен в противоположную сторону. Из рисунка 11–3 ясно, что при заряде конденсатора вектор Пойнтинга направлен внутрь конденсатора, и энергия запасается в его электрическом поле, а при разряде – наоборот, конденсатор отдает энергию.
Случай прямой синусоидальной электромагнитной волны.
Запишем выражения для напряженности электрического и магнитного поля прямой волны в произвольной точке при синусоидальном законе их изменения.
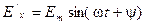 ;
; 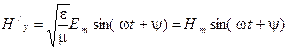
Замена аргумента (ω t +y) на принятый для бегущих волн аргумент (z-vt) осуществляется введением коэффициента «b»:
ω t + y = b (z – vt).
Записанное соотношение справедливо для любого момента времени. При t= 0 получаем y=b z. Тогда из того же соотношения можем записать:
ω t = – b vt, откуда 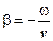
Учитывая изложенное, можем записать:
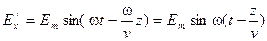 ;
; 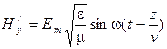 .
.
Бегущие волны записаны в обычной форме, из которой видно, что вдоль оси z они также распределены по синусоидальному закону. Картина распределения векторов напряженности электрического и магнитного поля для момента времени t= 0,5 T представлена на рисунке 11–4.
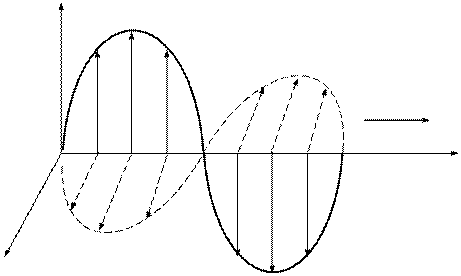 x Ex
x Ex
v
z
y Hy
Рисунок 11–4
В прямой синусоидальной плоско поляризованной электромагнитной волне векторы E и H перпендикулярны друг другу в любой точке пространства, имеют одинаковую начальную фазу и распространяются без затухания вдоль оси z.
Длина электромагнитной волны в диэлектрике.
Приращение координаты, на котором аргумент волны изменяется на 2p, называется длиной волны (l). Из соотношения bl=2p получим:

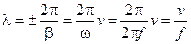 . Либо иначе:
. Либо иначе: 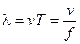
Так как скорость распространения электромагнитной волны в диэлектрике зависит только от его диэлектрических и магнитных свойств и не зависит от частоты передаваемого сигнала, то длина волны в диэлектрике обратно пропорциональна частоте сигнала. Длина электромагнитных волн в воздухе в зависимости от частоты (таблица 11–1) определяется из соотношения:
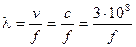
Таблица 11–1 Длина волны в воздухе для различных частот.
| Частота | Длина волны | Диапазон | Примечание |
| f | l | ||
| 105 гц =100 кГц | 3000 м | Длинные волны | |
| 106 гц =1 МГц | 300 м | Средние волны | |
| 107 гц =10 МГц | 30 м | Короткие волны | |
| 108 гц =100 МГц | 3 м | УКВ; FM; компьютер | ТВ - метровый диапазон |
| 109 гц =1000 МГц | 0,3 м | Мобильная связь | ТВ - дециметровый диапазон |