Методическое пособие
По решению задания №13
По математике
Елпанова А.Е.
Советы от автора при решении №13:
Если сомневаешься в формуле, то пользуйся справочными материалами.
2) В идеале необходимо привести к одному аргументу или свести к виду «произведение равно нулю», к квадратному уравнению в тригонометрии, к одному основанию, к удобной замене в смешанных уравнениях. Ни в коем случае нельзя делить на то, что равняется нулю!
3) Нужно помнить об ограничения! Их необходимо записывать в первую очередь и не забывать к ним возвратиться.
Записывай целые числа в связках корней разными буквами, не упусти логику решения.
5) Решай как тебе удобно – окружностью, неравенством – главное правильно!
Помни, что интервал всегда идет от меньшего угла к большему, в сторону возрастания угла.

№13 включает в себя:
- Тригонометрические уравнения
- Тригонометрические уравнения с ОДЗ
- Уравнения смешанного типа
- Логарифмические уравнения
- Показательные уравнения
- Иррациональные уравнения
- Рациональные уравнения
Тригонометрические уравнения
- Алгебраический метод.
Замена переменной и сведение к квадратному уравнению
Это универсальный способ. Применяется в любых уравнениях — степенных, показательных, тригонометрических, логарифмических, каких угодно. Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.
Рассмотрим уравнение: 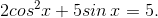
Преобразуем его, применив основное тригонометрическое тождество: 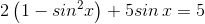
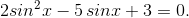
Заменяя sin x на t, приходим к квадратному уравнению: 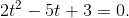
Решая его, получим: 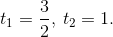
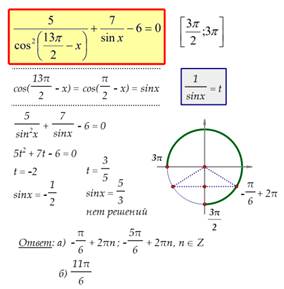
Теперь вспоминаем, что мы обозначили за t. Первый корень приводит нас к уравнению 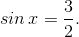 . Оно не имеет решений, поскольку
. Оно не имеет решений, поскольку 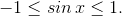
Второй корень даёт простейшее уравнение 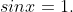
Решаем его:  Это и есть ответ.
Это и есть ответ.
- Разложение на множители.
Очень хорошо, если уравнение удаётся представить в таком виде, что в левой части стоит произведение двух или нескольких множителей, а в правой части — ноль. Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Сложное уравнение, таким образом, распадается в совокупность более простых.
- Начнём с уравнения
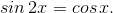
Применяем формулу синуса двойного угла: 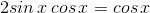
Ни в коем случае не сокращайте на косинус! Ведь может случиться, что cos x обратится в нуль, и мы потеряем целую серию решений. Переносим всё в одну часть, и общий множитель — за скобки:
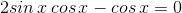
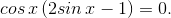
Полученное уравнение равносильно совокупности двух уравнений:
 и
и 
Решаем каждое из них и берём объединение множества решений.
Ответ: 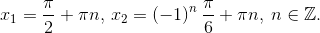
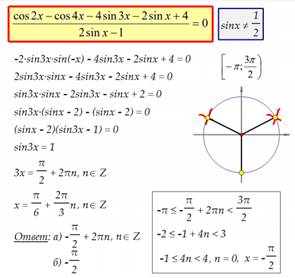
- Решить уравнение: cos 2 x + sin x · cos x = 1.
cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0,
sin x · cos x – sin 2 x = 0,
sin x · (cos x – sin x) = 0,
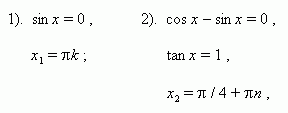
Ответ: х1=Пk; х2=П/4 + Пn
- Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.
cos 2 x + cos 6 x = 1 + cos 8 x,
2 cos 4 x cos 2 x = 2 cos ² 4 x,
cos 4 x · (cos 2 x – cos 4 x) = 0,
cos 4 x · 2 sin 3 x · sin x = 0,
1). cos 4 x = 0, 2). sin 3 x = 0, 3). sin x = 0,
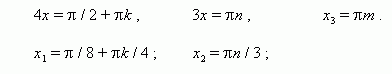
Ответ: х1=П/8 + Пk/4; х2=Пn/3; х3=Пm
- Приведение к однородному уравнению.
Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла. Чтобы решить однородное уравнение, необходимо:
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos (или sin) в старшей степени;
д) решить полученное алгебраическое уравнение относительно tg.
Решить уравнение: 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x,
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0,
tan 2 x + 4 tan x + 3 = 0, отсюда y 2 + 4 y +3 = 0,
корни этого уравнения: y 1 = -1, y 2 = -3, отсюда
1) tan x = –1, 2) tan x = –3,

Ответ: х1= -П/4 + Пk; х2= -arctg 3 +Пn
- Введение дополнительного угла.
Этот метод применяется для уравнений вида: a sin x + b cos x = c,
где a, b, c – коэффициенты; x – неизвестное.
Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.
- Рассмотрим уравнение
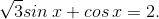
Делим обе части на 2: 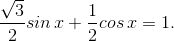
Замечаем, что 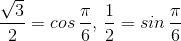 :
:

В левой части получили синус суммы: 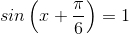 ,
,
откуда 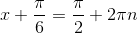 и
и 
Ответ: х1=П/3 + 2Пn
- Другой пример:
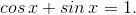
Делим обе части на 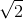
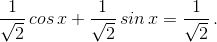
Сделаем теперь для разнообразия в левой части косинус разности:
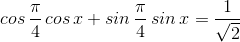
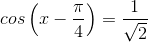
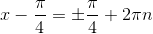
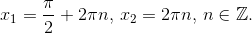
Ответ: х1=П/2 + 2Пk; х2=2Пn
- Преобразование произведения в сумму. Здесь используются соответствующие формулы.
Решить уравнение: 2 sin 2 x · sin 6 x = cos 4 x.
Преобразуем левую часть в сумму:
cos 4 x – cos 8 x = cos 4 x,
cos 8 x = 0,
8 x = П / 2 + П k,
x = П / 16 + П k / 8.
Ответ: х1=П/16 + Пk
Пример 1 Пример 2
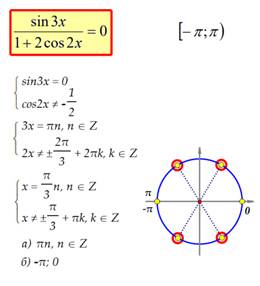
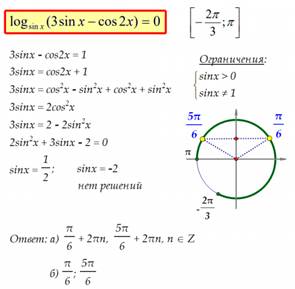
Пример 3 Пример 4
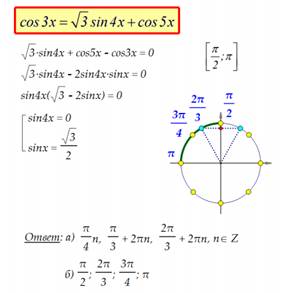
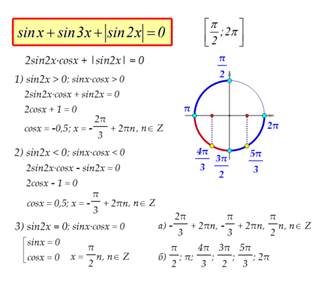
Пример 5 Пример 6