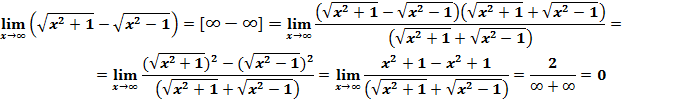Предел последовательности. Теоремы о сходящихся последовательностях
Число а называется пределом последовательности ( ), если для любого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство:
), если для любого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство:
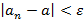
Тот факт, что число а является пределом последовательности ( ), записывается в виде
), записывается в виде

Последовательность, имеющая предел, называется сходящейся, а последовательность, не имеющая предела, – расходящейся.
Теоремы о сходящихся последовательностях:
Теорема 1. Если последовательность сходится, то она имеет только один предел.
Теорема 2. Если последовательность сходится, то она ограничена.
Теорема 3. Если последовательности  и
и  сходятся то
сходятся то


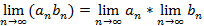
Если, кроме того, 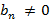 для любого n и
для любого n и  , то
, то

Из ТЕОРЕМЫ2 следует, что любая неограниченная последовательность является расходящейся.
Из ТЕОРЕМЫ3 следует, что постоянную можно выносить за знак предела, т.е. если последовательность ( ) сходится, то
) сходится, то

Предел функции
Напомним, что любой интервал, содержащий точку а, называется окрестностью точки а.
Пусть функция f(x) определена в некоторой окрестности точки а, за исключением, быть может, самой точки а, т.е. никаких предположений о том, определена ли функция в точке а или нет, не делается.
Число b называется пределом функции f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа ε найдется такое положительное число δ, что при всех  , удовлетворяющей неравенству
, удовлетворяющей неравенству  , будет выполняться неравенство
, будет выполняться неравенство
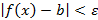
Для обозначения того, что число b есть предел функции f(x) при х стремящемся к a, пишут
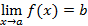
Для функций, имеющих предел в точке, справедлива теорема, аналогичная теореме о сходящихся последовательностях.
Теорема. Пусть при х, стремящемся к а, существуют пределы функций f(x) и g(x). Тогда при х, стремящемся к а, существуют также пределы суммы, разности и произведения этих функций, при этом



Если, кроме того,  для любого n и
для любого n и  , то
, то
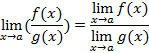
Замечательные пределы и их следствия
Первый замечательный предел:

Следствия первого замечательного предела:
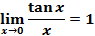
| 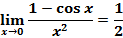
|

| 
|

| 
|
Второй замечательный предел:

Следствия второго замечательного предела:

| 
|

| 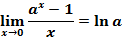
|

| 
|

Определенность и неопределенность в пределах функций
При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.
Перечислим все основные виды неопределенностей: ноль делить на ноль  , бесконечность делить на бесконечность
, бесконечность делить на бесконечность  , ноль умножить на бесконечность
, ноль умножить на бесконечность  , бесконечность минус бесконечность
, бесконечность минус бесконечность  , единица в степени бесконечность
, единица в степени бесконечность  , ноль в степени ноль
, ноль в степени ноль 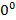 , бесконечность в степени ноль
, бесконечность в степени ноль 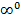 .
.
ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Неопределенность вида 
Пример 1
Вычислить предел 
Подставив напрямую значение  , убеждаемся, что данная функция имеет неопределенность
, убеждаемся, что данная функция имеет неопределенность  в точке
в точке  . Разложив числитель на множители получаем
. Разложив числитель на множители получаем

Пример 2
Вычислить предел 
Функция имеет неопределенность  в точке
в точке  . Разложим числитель и знаменатель на множители
. Разложим числитель и знаменатель на множители

Аналогично,

Таким образом, предел равен

Пример 3
Вычислить предел 
Перепишем знаменатель в виде 
и разложим его как разность кубов

В результате можно найти
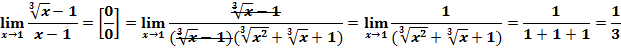
Пример 4
Вычислить предел 
Сделаем замену переменной:  .Тогда
.Тогда  при
при  Получаем:
Получаем:

По фурмулам приведения получаем

Приводим к 1му замечательному пределу

Пример 5
Вычислить предел 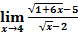
Для вычисления предела избавимся от иррациональностей в числителе и знаменателе, умножив их на соответствующие сопряженные выражения.
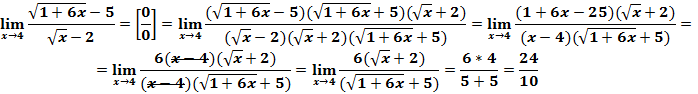
Пример 6
Вычислить предел 
Сделаем замену переменной:  .Тогда
.Тогда  при
при  Получаем:
Получаем:

Приводим данное выражение к одному из следтсвий 2го замечательного предела

Неопределенность вида 
Пример 7
Вычислить предел 
Подстановка  показывает, что функция имеет неопределенность
показывает, что функция имеет неопределенность  . Вынесем в числителе и знаменателе
. Вынесем в числителе и знаменателе  (как x в наивысшей степени числителя и знаменателя). В результате получаем
(как x в наивысшей степени числителя и знаменателя). В результате получаем

Неопределенность вида 
Пример 8
Вычислить предел 
Если  , то
, то  и
и 
Таким образом, здесь мы имеем дело с неопределенностью типа  . Умножим и разделим данную иррациональную функцию на сопряженное выражение.
. Умножим и разделим данную иррациональную функцию на сопряженное выражение.