Лекция 15. Производная.
Понятие производной.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Дадим аргументу
. Дадим аргументу  некоторое приращение
некоторое приращение  (положительное или отрицательное). Тогда функция
(положительное или отрицательное). Тогда функция  получит приращение
получит приращение  . Рассмотрим отношение
. Рассмотрим отношение  .
.
Определение 15.1. Конечный предел отношения приращения  функции
функции  к приращению аргумента
к приращению аргумента  при условии
при условии  называется производной функции
называется производной функции  в точке
в точке  .
.
Этот предел обозначается символом  :
:
 . (15.1)
. (15.1)
Наряду с обозначением производной 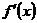 в произвольной точке x употребляются и другие обозначения:
в произвольной точке x употребляются и другие обозначения:  ,
,  ,
,  .
.
Конкретные значения производной при  обозначаются через
обозначаются через  ,
,  ,
,  .
.
Формулу (15.1) можно записать в виде
 . (15.2)
. (15.2)
J Пример 15.1. 
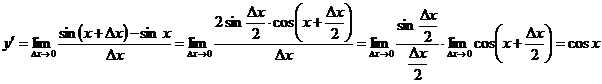 . J
. J
Геометрическая интерпретация производной.
Пусть на плоскости xOy задана кривая, описываемая уравнением  . Проведём касательную к кривой в точке
. Проведём касательную к кривой в точке  . Возьмём на кривой точку M1 и проведём секущую M0M1 (рис. 15.1). При изменении точки M1 положение секущей будет меняться.
. Возьмём на кривой точку M1 и проведём секущую M0M1 (рис. 15.1). При изменении точки M1 положение секущей будет меняться.

| Рис. 15.1. |
Определение 15.2. Если при стремлении точки 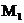 к фиксированной точке
к фиксированной точке  секущая
секущая  не зависимо от способа стремления точки
не зависимо от способа стремления точки 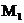 к точке
к точке  стремится к одному и тому же предельному положению, то прямая, являющаяся этим предельным положением, называется касательной к кривой в точке
стремится к одному и тому же предельному положению, то прямая, являющаяся этим предельным положением, называется касательной к кривой в точке  .
.
Получим уравнение этой касательной. Обозначим координаты точки M1 через  и пусть
и пусть  – угол наклона секущей к оси Ox. Тогда (см. рис. 15.1) угловой коэффициент секущей M0M1 равен
– угол наклона секущей к оси Ox. Тогда (см. рис. 15.1) угловой коэффициент секущей M0M1 равен
 . (15.3)
. (15.3)
Если же устремить точку M1 к точке M0, то есть устремить  к нулю, то в случае существования производной
к нулю, то в случае существования производной  угол
угол  будет стремиться к некоторому пределу
будет стремиться к некоторому пределу  , где
, где  . Следовательно, прямая, составляющая с положительным направлением оси Ox угол
. Следовательно, прямая, составляющая с положительным направлением оси Ox угол  и проходящая через точку M0 и будет касательной. Её угловой коэффициент
и проходящая через точку M0 и будет касательной. Её угловой коэффициент  .
.
Запишем уравнение касательной к графику  в точке
в точке  :
:
 . (15.4)
. (15.4)
Определение 15.3. Прямая называется перпендикулярной к кривой в точке  , если она перпендикулярна касательной к кривой в точке
, если она перпендикулярна касательной к кривой в точке  . Эта прямая называется также нормалью к этой кривой.
. Эта прямая называется также нормалью к этой кривой.
Угловой коэффициент нормали к кривой в точке M0  при
при  , и уравнение нормали к графику функции, проходящему через точку
, и уравнение нормали к графику функции, проходящему через точку  запишется в следующем виде:
запишется в следующем виде:
 . (15.5)
. (15.5)
Если  , то уравнение нормали
, то уравнение нормали  .
.
☼ Замечание 15.1. Если в точке 
 и
и  , то касательная к кривой
, то касательная к кривой  в точке
в точке  существует, она вертикальна и её уравнение
существует, она вертикальна и её уравнение  . Уравнение соответствующей нормали
. Уравнение соответствующей нормали  .☼
.☼
Физический смысл производной.
1) Пусть задан закон движения точки 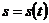 . Средняя скорость движения
. Средняя скорость движения  . Мгновенная скорость движения
. Мгновенная скорость движения  .
.
Среднее ускорение движения 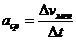 . Мгновенное ускорение движения
. Мгновенное ускорение движения  .
.
2) Сила тока в момент времени t:  , где
, где  – количество электричества.
– количество электричества.
3)  – количество вещества, вступающего в химическую реакцию за время t. Скорость химической реакции в момент времени t:
– количество вещества, вступающего в химическую реакцию за время t. Скорость химической реакции в момент времени t:  .
.
4)  – масса неоднородного стержня между точками
– масса неоднородного стержня между точками  и
и  . Линейная плотность стержня в точке x есть
. Линейная плотность стержня в точке x есть  .
.
5) Барометрическая формула (зависимость атмосферного давления от высоты над уровнем моря).
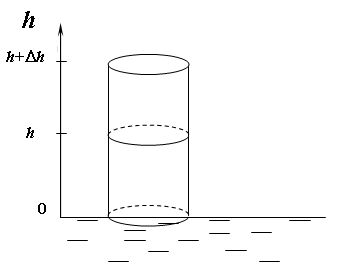
|  – давление воздуха на высоте h – давление воздуха на высоте h
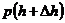 – давление воздуха на высоте – давление воздуха на высоте 
 – плотность воздуха на высоте h – плотность воздуха на высоте h
 , , 


|
С учётом закона Менделеева-Клапейрона  (
( – количество вещества, m – масса воздуха, M – молярная масса воздуха, R – универсальная газовая постоянная), получаем
– количество вещества, m – масса воздуха, M – молярная масса воздуха, R – универсальная газовая постоянная), получаем  . Обозначая
. Обозначая 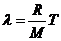 , получаем далее:
, получаем далее:
 ,
,  ,
,  .
.
Так как производные равны, то  , где
, где  – давление воздуха на уровне моря. Окончательно, барометрическая формула выглядит как
– давление воздуха на уровне моря. Окончательно, барометрическая формула выглядит как
 .
.