МЕТОДЫ И СРЕДСТВА НАУЧНЫХ ИССЛЕДОВАНИЙ

Методические указания к практическим работам с элементами УИРС

для студентов по направлению подготовки бакалавров 35.03.02 – Технология

лесозаготовительных и деревообрабатывающих производств, профиль –Технологии мебели, материалов и изделий из древесины,

профиль – Дизайн мебели

 

 

Воронеж 2018

 

УДК 674

Кантиева, Е. В. Методы и средства научных исследований [Текст]: методические указания к практическим работам с элементами УИРС для студентов по направлению подготовки бакалавров 35.03.02 – Технология лесозаготовительных и деревообрабатывающих производств, профиль - Технологии мебели, материалов и изделий из древесины, профиль – Дизайн мебели / Е. В. Кантиева М-во образования и науки РФ. - ФГБОУ ВО «ВГЛТУ»; – Воронеж 2018. – 57 с.

 

Печатается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № от)

 

 

Рецензент: директор

ООО «Перфект – Воронеж» Золотухин Д. Ю.

 

 

Оглавление

Практическое занятие № 1. Исследование статистических характеристик

толщины древесных материалов……………………………………………………4

Практическое занятие № 2. Корреляционный анализ и нахождение линейной регрессионной зависимости ………………………………………………………12

Практическое занятие № 3. Нахождение нелинейных регрессионных зависимостей с одной независимой переменной …………………………………………..16

Практическое занятие № 4. Исследование объектов методом полного факторного эксперимента ……………………………………………………………………21

Практическое занятие № 5. Исследование объектов методом дробного факторного эксперимента …………………………………………………………………30

Практическое занятие № 6. Получение математической модели объектов методом униформ-ротатабельного планирования ……………………………………36

 

 

Практическое занятие № 1

 

Исследование статистических характеристик толщины древесных материалов

 

Цель работы: Изучить методики первичной статистической обработки эмпирических данных.

Изучение статистической обработки проводится на примере толщины древесных материалов.

Чтобы получить исходные данные для выполнения работы, необходимо замерить толщину 60…70 образцов какого-либо древесного материала (шпон лущеный, шпон строганый, фанера, древесноволокнистая плита, древесностружечная плита, декоративный бумажно-слоистый пластик и т.п.).

Результат единичного измерения является случайной величиной Х_i.

Случайные величины объединяются в статистические совокупности случайных величин. Различают генеральные и выборочные статистические совокупности.

Статистическая совокупность, содержащая в себе все возможные значения случайной величины, называется генеральной статистической совокупностью.

Выборочной статистической совокупностью называется совокупность, в которой содержится только некоторая часть элементов генеральной совокупности. Иначе часть генеральной совокупности называется выборочной статистической совокупностью или выборкой. Число случайных величин, вошедших в нее, называется объемом выборки и обозначается через n.

По результатам экспериментов практически всегда встречаются с выборочной, а не с генеральной совокупностью.

Выборка характеризуется следующими статистическими характеристиками:

 

Среднее выборочное 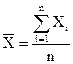(1)

Выборочная дисперсия

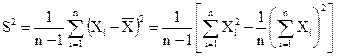(2)

Среднее квадратическое отклонение 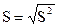(3)

Коэффициент вариации 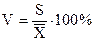(4)

Ошибка среднего 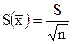(5)

Показатель точности среднего 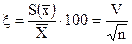(6)

Чтобы упростить вычисления 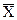и S², а также для построения гистрограммы, выборку разбивают на интервалы. Число интервалов k зависит от объема выборки и определяется по формуле

 

k = 1 + 3,2 lg n, (7)

 

где n – объем выборки.

Число интервалов k необходимо округлять до целого числа.

В выборке определяют минимальное (Х_min) и максимальное (X_max) значения случайной величины и находят зону рассеяния R

 

R = X_max - Х_min. (8)

 

Если разделить зону рассеяния на число интервалов, то можно определить длину или шаг интервала h

 

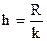. (9)

Первый интервал начинается с Х_min и заканчивается прибавлением длины интервала. Второй интервал начинается с Х_min + h и заканчивается Х_min + 2h и т.д. Последний интервал заканчивается Х_max.

Необходимо определить середину интервала Х_j и частоты m_j – число случайных величин, попадающих в каждый интервал. Сумма частот всех интервалов равна объему выборки.

Данные удобно свести в табл. 1.

 

Таблица 1

Данные для построения гистограммы и вычисления

статистических характеристик

№ инт.	Интервал	Середина интервала, Хj	Частоты, mj	mjxj	mjxj2
свыше	до	в условных обозначениях	в цифрах

 

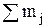
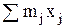
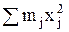
Затем в табл. 1 заполняют еще две колонки с расчетом произведений m_jx_j и m_jx_j², суммы которых необходимы для расчета статистических характеристик.

 

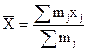(10)

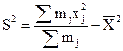. (11)

Остальные статистические характеристики вычисляют по формулам 3…6.

По экспериментальным частотам можно построить график распределения частот по интервалам – гистограмму, представляющую собой ступенчатый график.

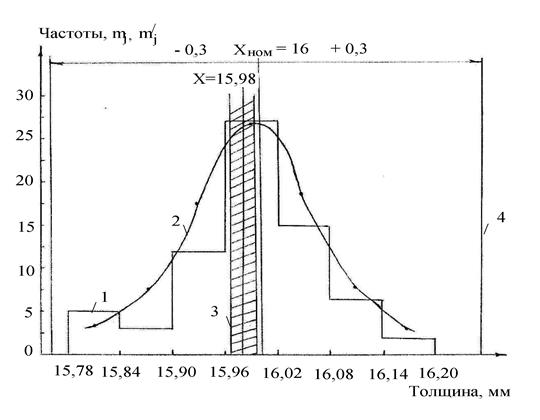
Рис. 1 Характеристики экспериментального и теоретического распределения случайных величин: 1 – гистограмма;

2 – теоретическая кривая;

3 – доверительный интервал;

4 – ГОСТовский интервал.

Затем проводят проверку однородности наблюдений, которая заключается в выявлении грубых ошибок (или промахов экспериментатора). Это значения случайных величин, которые резко выделяются из выборки. На грубые ошибки проверяют минимальное и максимальное значения случайных величин выборки по формулам:

 

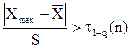
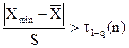, (12)

 

где t_1-q(n) – квантиль распределения максимального относительного отклонения, зависящий от объема выборки n и уровня значимости q. Принимаем q равным 0,05. Значения квантилей t_1-q(n) приведены в прил. 1.

Если условие 12 выполняется, проверяемое значение случайной величины является грубоошибочным и его следует исключить из выборки. В этом случае объем выборки уменьшается на число грубоошибочных величин. После отбрасывания грубоошибочных значений случайных величин необходимо заново определить максимальное и минимальное значения толщины в выборке, заново разбить ее на интервалы и определить статистические характеристики, снова проверить выборку на наличие грубоошибочных наблюдений.

Как уже было сказано выше, все значения толщины материала в выборке являются случайными, и случайными также будут выборочные статистические характеристики. Они отличаются от истинных значений - генерального среднего или математического ожидания, генеральной дисперсии и др.

Определить истинное значение статистической характеристики по выборке невозможно, но можно определить интервал, в котором оно лежит.

Истинное значение среднего а_х отличается от выборочного среднего 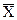на какую-то погрешность e

 

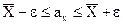(13)

 

Погрешность рассчитывается как

 

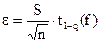, (14)

где t_1-q(f) – квантиль t-распределения Стьюдента, который зависит от принятого уровня значимости q и числа степеней свободы f = n - 1. Значения t_1-q(f) приведены в прил. 2.

Числом степеней свободы f выборки объемом n называется разность между объемом выборки и числом связей, наложенных на эту выборку.

Подставив выражение e в формулу 13, получаем

 

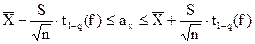, (15)

Границы интервала (формула 15) определяются доверительной вероятностью р.

Доверительной вероятностью или уровнем достоверности является возможность совершения какого-либо события. В данном случае это вероятность нахождения истинного результата в указанных границах. Соответствующие доверительной вероятности пределы называются доверительными границами, а образуемый ими интервал – доверительным интервалом. На практике в качестве доверительной вероятности берут значения p, равные 0,95; 0,99; 0,999.

Наибольшее значение вероятности, несовместимой со случайностью события, называется уровнем значимости q. Другими словами, уровень значимости есть максимум таких вероятностей, при которых событие можно считать практически невозможным. Наиболее употребительны уровни значимости q, равные 0,05; 0,01; 0,001.

Очевидно, что сумма доверительной вероятности и уровня значимости p + q = 1.

При одной и той же доверительной вероятности границы доверительного интервала будут зависеть и от объема выборки, и от рассеяния значений случайной величины относительно среднего. А именно, с ростом объема выборки и уменьшением среднего квадратического отклонения среднее выборочное приближается к истинному значению.

Доверительный интервал следует нанести на график.

Далее необходимо определить, подчиняется ли исследуемая нами выборка закону нормального распределения Гаусса.

Для этого вычисляют теоретические значения частот m_j по формулам:

 

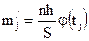, (16)

где 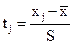, (17)

а j(t_j) приведены в прил. 3.

Вычисления удобно производить в табл. 2.

 

 

Таблица 2

Построение кривой нормального распределения Гаусса

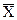
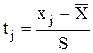
№ инт.	Середина интервала, xj	Эмпирические частоты, mj	xj -		j(tj)		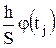Теоретические частоты,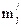

 

Теоретические частоты также наносят на график и получают теоретическую кривую распределения (рис. 1, кривая 2).

Далее проверяют согласованность теоретической и экспериментальной кривых по критерию Пирсона. Критерий Пирсона среди различных критериев согласия является наиболее строгим и надежным для оценки степени различия эмпирического и теоретического распределений. Он рассчитывается по формуле

 

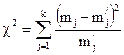, (18)

 

где k – число интервалов, на которые разбиты опытные данные.

Расчеты удобно свести в табл. 3.

При вычислениях необходимо объединить интервалы с частотами, встречаемость которых менее 5.

Затем по прил. 4 находят критическое (табличное) значение критерия Пирсона c_q²(f). Оно определяется в зависимости от уровня значимости q и от числа степеней свободы f = k – r – 1, где k – число интервалов после объединения, а r – число параметров теоретической функции распределения Гаусса (r = 2).

 

 

Таблица 3

Вычисление критерия Пирсона

№ инт.	mj

 

 

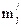
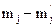
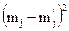
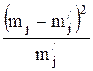
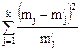
Далее сравнивают расчетное значение критерия Пирсона с критическим

 

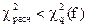. (19)

 

Если расчетное значение меньше критического, то экспериментальная и теоретическая кривые согласуются и выборка подчиняется закону нормального распределения Гаусса.

Каждый древесный материал производится по ГОСТ и имеет определенную номинальную толщину и допускаемые отклонения (прил. 5). Наносят номинальную толщину на график и определяют количество образцов (в %), соответствующее ГОСТу, принимая объем выборки за 100 %.

Проводят проверку произведенных расчетов на ЭВМ по программе STAT и делают выводы по работе.

 

 

Практическое занятие № 2

 

Корреляционный анализ и нахождение линейной регрессионной

зависимости

 

Цель работы: провести корреляционный анализ между двумя изменяемыми величинами и определить зависимость между ними в виде линейной регрессии.

Объектом исследования является процесс продольного пиления древесины на круглопильном станке ЦДК4-3. В этом процессе исходные данные являются постоянными, кроме одного варьируемого фактора. Этим фактором может быть порода древесины, влажность, толщина материала, скорость подачи, число зубьев пилы в зависимости от варианта задания. Результатом исследования является мощность резания или шероховатость поверхности. Исходные данные для выполнения работы приведены в табл. 4.

Проводится компьютерный эксперимент (программа PIL). Варьируемый фактор принимает шесть различных значений, т.е. проводится шесть опытов. Каждый опыт повторяется пять раз (число наблюдений m = 5), из этих значений получают среднее значение 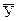и дисперсии S_i² для каждого опыта (построчные дисперсии), которые далее используются в расчетах.

 

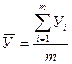(20)

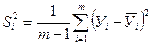(21)

 

Необходимо провести корреляционный анализ, то есть определить, связано ли изменение выходной величины У с изменением переменного входного фактора Х, является ли У функцией от Х (У = f(X)), и проверить, имеется ли линейная зависимость между этими величинами.

 

 

Таблица 4

Продольное пиление на круглопильном станке ЦДК4-3

Компьютерный эксперимент (программа PIL)

 

№ задания	Постоянные факторы	Переменный фактор
P	W	H	U	TP	D	Z	S	T
	-							1,8		P
		-						2,2		W = 8-25
				-				2,8		U = 10-50
			-					2,8		H = 25-50
	-	-		-				-	-	U = 10-50
	-	-					-	-	-	Z = 36-80
	-							2,8		P
		-						2,8		W = 8-25
				-				2,5		U = 8-60
			-					2,5		H = 25-50
	-	-		-				-	-	U = 8-60
	-	-					-	-	-	Z = 24-60
	-							2,5		P
		-						2,8		W = 8-25
				-				2,0		U = 8-40
			-					2,4		H = 30-80
	-	-		-				-	-	U = 8-40
	-	-					-	-	-	Z = 48-72
	-							2,8		P
		-						2,2		W = 8-25
				-				2,4		U = 12-60
			-					2,8		H = 22-60
	-	-		-				-	-	U = 12-60
	-	-					-	-	-	Z = 36-72
				-				2.8		U = 18-60
№ заданий	Вид эксперимента
1,7,13,19 2,8,14,20 3,9,15,21,25 4,10,16,22 5,11,17,23 6,12,18,24	1 – Мощность резания от породы древесины 2 – Мощность резания от влажности древесины 3 – Мощность резания от скорости подачи 4 – Мощность резания от толщины материала 5 – Шероховатость поверхности от скорости подачи 6 – Шероховатость поверхности от числа зубьев пилы

Условные обозначения

Р – порода древесины (1 – ель, 2 – сосна, 3 – береза, 4 – лиственница, 5 – бук, 6 – дуб);

ТР – тип пилы (1 – плоская с разведенными зубьями, 2 – плоская с плющенными зубьями, 3 – дисковая с твердосплавными пластинками);

W – влажность древесины, %; D – диаметр пилы, мм;

Н – толщина материала, мм; S – толщина пилы, мм;

U – скорость подачи, м/мин; Z – число зубьев пилы;

Т – продолжительность работы пилы, час.

Корреляционный анализ проводится путем расчета коэффициента корреляции r(X,У) по формуле

 

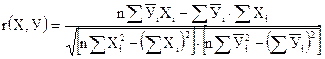(22)

 

Коэффициент корреляции имеет определенный физический смысл. Это показатель, по которому количественно оценивают, насколько связь между случайными величинами Х и У близка к линейной зависимости. Если значение r(X,У) близко к ± 1, то зависимость между Х и У близка к линейной; если r(X,У) мало отличается от нуля, между Х и У никакой коррелятивной связи нет.

Для расчета коэффициента корреляции удобно составить табл. 5.

 

Таблица 5

Данные для вычисления коэффициента корреляции

№ опыта	Хi		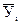Xi2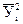

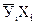
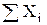
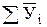
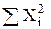
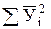
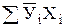
После вычисления коэффициента корреляции необходимо проверить значимость отличия его от нуля. Для этого используется оценка

 

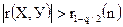, (23)

 

где r_1-q/2(n) – квантиль r-распределения при уровне значимости q. Он зависит от объема выборки n. Его значения приведены в прил. 6.

Если расчетный коэффициент корреляции больше табличного, то считаем, что зависимость между Х и У будет линейной.

Затем рассчитывают дисперсию воспроизводимости S_У² как среднее из шести построчных дисперсий.

 

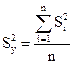(24)

 

Число степеней свободы построчной дисперсии f_i = m – 1.

Число степеней свободы дисперсии воспроизводимости f_у = n (m – 1).

Уравнение линейной регрессионной зависимости имеет вид

 

У = а + bХ, (25)

 

где а и b – коэффициенты регрессии.

Сначала определяют значения коэффициентов а и b по формулам:

 

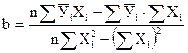; (26)

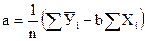. (27)

 

Подставляя в уравнение найденные значения коэффициентов а и b и значения Х из эксперимента, рассчитывают теоретические значения 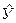для каждого из шести опытов.

Затем рассчитывают дисперсию адекватности S²_ад (ее также называют остаточной дисперсией) по формуле

 

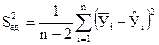(28)

 

Число степеней свободы дисперсии адекватности f_ад = n – 2.

Чтобы установить, насколько точно полученное приближенное уравнение регрессии соответствует истинной регрессии, не требуется ли в найденное уравнение ввести какие-либо дополнительные члены, проводят проверку адекватности модели. Адекватность модели проверяют с помощью квантиля распределения Фишера (критерия Фишера) F_1-q(f_ад, f_у) по формуле

 

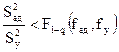. (29)

 

Значения квантиля распределения Фишера F_1-q(f_ад, f_у) приведены в прил. 7. Его выбирают в зависимости от уровня значимости q и числа степеней свободы дисперсий адекватности и воспроизводимости.

Если выполняется условие 29, то уравнение линейной регрессии признается адекватным, то есть зависимость У от Х имеет линейный вид. В противном случае уравнение регрессии следует искать в другом виде (какой-либо нелинейной функции).

Для контроля вычислений в данной работе следует использовать компьютерную программу KORR.

 

 

Практическое занятие № 3

 

Нахождение нелинейных регрессионных

зависимостей с одной независимой переменной

 

Между двумя случайными величинами может существовать зависимость не только в линейном виде, но и в виде различных нелинейных функций.

Цель работы: определить конкретный вид зависимости, связывающей случайные величины Х и У.

В качестве исходных эмпирических данных для выполнения работы следует использовать результаты компьютерного эксперимента из предыдущей работы (шесть пар значений варьируемого фактора Х и средних значений выходной величины У).

Нелинейные зависимости между случайными величинами Х и У могут иметь разную форму и выражаться самыми разнообразными уравнениями. Графики некоторых элементарных функций, по которым часто осуществляют выравнивание эмпирических значений, приведены в табл. 6.

Таблица 6

Виды некоторых функций

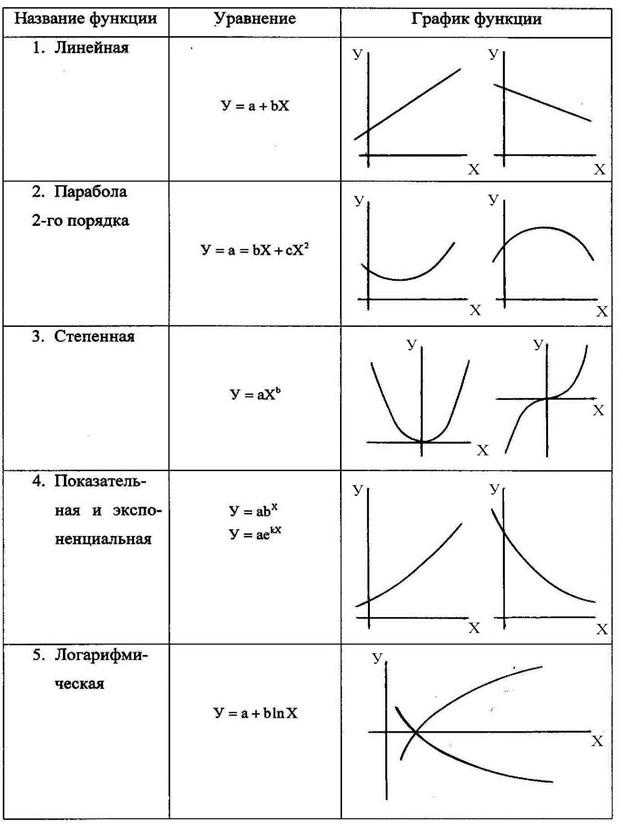
Суть работы состоит в следующем. Поочередно рассматриваются несколько различных нелинейных функций. По приведенным ниже уравнениям рассчитываются коэффициенты a,b и c. В каждую функцию подставляют числовое значение найденных коэффициентов и значение варьируемого фактора Х. Таким образом получают теоретические значения выходной величины 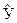. Затем для каждой функции находят основную ошибку. Рассчитав теоретические значения 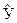по нескольким функциям, сравнивают между собой основные ошибки. Функция, у которой основная ошибка будет наименьшей, обладает наилучшим приближением к эмпирическим значениям выходной величины У.

Работу выполняют следующим образом. Заполняют табл. 7 для проведения последующих расчетов.

Таблица 7

Вычисление параметров уравнений регрессии

i	Хi	Уi	Xi2	Xi3	Xi4	УiXi	УiXi2
Сумма
i	ln Xi	(ln Xi)2	ln Уi	Xi ln Уi	Уi ln Xi	ln Xi × ln Уi
Сумма

 

Рассмотрим некоторые уравнения нелинейных функций. Многие из нелинейных зависимостей могут быть преобразованы к линейному виду, например, путем логарифмирования. Соответствующим образом преобразуются и расчетные формулы для определения коэффициентов уравнения.

1. Рассмотрим показательную функцию. Она выражается уравнением

У = ab^X. (30)

Преобразуем ее к линейному виду путем логарифмирования

ln У = ln a + X ln b. (31)

Логарифмы коэффициентов находим по формулам:

 

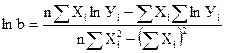; (32)

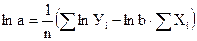. (33)

Подставляя найденные значения коэффициентов и значения Х для каждого опыта в уравнение 31, находим логарифмы 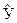и от них переходим к значениям 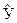по формуле У = e^{ln У}.

Основную ошибку вычисляем по сумме квадратов отклонений эмпирических данных от найденных теоретических значений по формуле

 

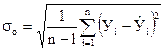, (34)

 

где l – количество коэффициентов регрессии функции У = f (Х).

2. Рассмотрим степенную функцию

У = aX^b. (35)

После логарифмирования имеем

ln У = ln a + b ln X. (36)

Коэффициенты находим по формулам:

 

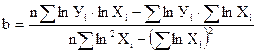; (37)

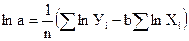. (38)

 

Подставляя найденные значения в уравнение 36, находим логарифмы 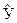и от них переходим к теоретическим значениям 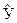и рассчитываем основную ошибку.

3. Рассмотрим логарифмическую функцию

У = a +b ln X. (39)

Коэффициенты находим по формулам:

 

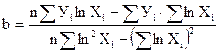; (40)

(41)

и рассчитываем теоретические значения 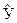по уравнению 39. Опять рассчитываем основную ошибку.

4. Рассмотрим параболическую функцию

У = a + bX +cX². (42)

Коэффициенты находим по формулам:

 

;

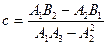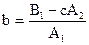; (43)

,

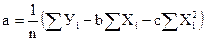где

 

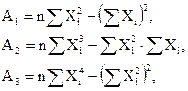
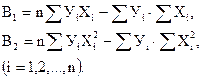
По уравнению 42 рассчитываем теоретические значения У и определяем основную ошибку.

5. Линейная функция

У = a + bX

была рассмотрена в предыдущей работе. Используя полученные теоретические значения У, рассчитываем основную ошибку.

Сравниваем полученные основные ошибки и делаем вывод о степени приближения эмпирических значений к рассмотренным функциям. Необходимо построить график зависимости эмпирических значений У и теоретических значений 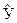по функции, обладающей наименьшей основной ошибкой, от варьируемого фактора Х.

Для контроля вычислений в данной работе следует использовать компьютерную программу EXPEN 4.

 

 

Практическое занятие № 4

 

Исследование объектов методом полного факторного эксперимента

 

Цель работы – получение математической модели объекта в виде уравнения регрессии первого порядка методом полного факторного эксперимента.

Полный факторный эксперимент (ПФЭ) – один из методов планирования многофакторных экспериментов, предназначенных для нахождения математической модели объекта. ПФЭ называют такой эксперимент, при котором число уровней варьирования всех факторов одинаково и может включать в себя все возможные комбинации этих уровней.

В ПФЭ число уровней варьирования факторов два: верхний и нижний. Верхним уровнем называется максимальное значение фактора (V_{i max}), нижним – минимальное значение фактора (V_{i min}).

Середина диапазона варьирования называется основным уровнем (V_i⁽⁰⁾) и определяется по формуле

 

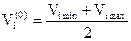(44)

 

Интервал варьирования факторов (D V_i)

 

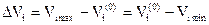(45)

 

Значения V_i – это натуральные значения факторов.

Процедуру обработки данных эксперимента можно вести с использованием обозначенных натуральных значений факторов, но она существенно упрощается, если вместо натуральных пользоваться кодированными значениями факторов. Связь между кодированными и натуральными значениями факторов выглядит следующим образом:

 

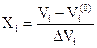, (46)

 

где Х_i – кодированное значение фактора;

V_i – текущее натуральное значение фактора (оставляется в буквенном обозначении).

Натуральному значению фактора на верхнем уровне V_{i max} соответствует кодированное (+ 1), на нижнем уровне V_{i min} – (-1), на основном V_i⁽⁰⁾ – (0).

В данной работе объектом исследования является процесс продольного пиления древесины на круглопильном станке ЦДК4-3. Исходные данные содержат в себе постоянные (порода древесины, ее влажность, тип, диаметр, толщина и число зубьев пилы) и три переменных фактора (толщина материала, скорость подачи и продолжительность работы пилы). Результатом исследования является мощность резания.

Значения постоянных и переменных факторов приведены в табл. 8.

Для заданных значений переменных факторов, пользуясь формулами 44-46, определить уровни и интервалы варьирования, а также написать формулы пересчета от натуральных значений факторов к кодированным. Полученные результаты следует занести в табл. 9.

Далее необходимо составить матрицу планирования (ее еще называют планом эксперимента), включающую в себя все возможные сочетания кодированных значений факторов на нижних и верхних уровнях. Количество опытов в матрице ПФЭ равно

 

 

N = 2^k, (47)

где k – количество варьируемых факторов.

 

 

Таблица 8

Продольное пиление на круглопильном станке ЦДК4-3

Компьютерный эксперимент (PFPP1)

№ задания	Постоянные факторы	Варьируемые факторы
P	W	TP	D	Z	S	H	U	T
						2,2	25-65	8-40	1-6
						2,5	28-90	10-50	1-6
						2,8	25-100	12-60	1-6
						2,4	25-50	8-60	1-6
						2,5	32-70	10-56	1-6
						2,8	28-50	12-52	1-6
						2,2	32-80	10-40	1-6
						2,8	25-60	10-60	1-6
						2,2	40-100	8-48	1-6

Поделиться: